3-D High-Resolution ISAR Imaging for Noncooperative Air Targets | IEEE Journals & Magazine | IEEE Xplore
Abstract:This article uses the inverse synthetic aperture radar (ISAR) imaging method to present real-world tests on 3-D radar imaging of noncooperative air targets. Initially, th...View more
Metadata
Abstract:
This article uses the inverse synthetic aperture radar (ISAR) imaging method to present real-world tests on 3-D radar imaging of noncooperative air targets. Initially, the fundamentals of 3-D ISAR are introduced. This is followed by a discussing of the challenges of obtaining high-quality 3-D radar images. An essential feature of the applied method is its basis on the back-projection family of techniques, eliminating the need for iterative image reconstruction. These theoretical concepts are validated using both simulations and real-life signals. This article also provides insights into the measurement campaign and the signal processing techniques applied to achieve the presented results.
Page(s): 4194 - 4207
Date of Publication: 23 January 2024
Figures are not available for this document.
In The modern battlefield, air target imaging and classification are crucial tasks. The primary sensors used for these purposes are optical and radar sensors. The advantage of optical sensors is their high resolution; however, the disadvantage is their high dependence on weather conditions, such as fog, cloudy weather, rain, snow, or image dispersion due to air temperature differences. Lower resolutions to the optical images characterize radar imaging. However, it allows the creation of a target image independently of the weather conditions, enabling day and night operation. The resolution of the radar imaging depends on the bandwidth of the emitted signal. Nowadays, a centimeter resolution is easily achievable using GHz and more bandwidths [1], [2], [3], [4], [5], [6], [7]. Such a resolution is sufficient regarding air target classification [8], [9], [10], [11]. The inverse synthetic aperture radar (ISAR) technique, developed in the last century [12], [13], is most often used for the radar imaging of air targets. The 2-D ISAR has now entered the maturity stage, which can be seen in various advanced and highly efficient methods, e.g., [14], [15], [16], [17], [18], and [19]. Over recent years, many different demonstrators of this technology have been developed, and the 2-D ISAR has also been implemented in final radar products offered by the industry [20], [21], [22].
As 2-D ISAR imaging is a mature technology, in recent years, researchers have been focusing on novel 3-D ISAR imaging techniques [23], [24], [25], [26]. Up to now, 3-D radar imaging has been used mainly in the remote sensing applications of Earth imaging, where the interferometric synthetic aperture radar (InSAR) method has been applied [27], [28], [29], [30], or in tomography imaging [31]. The 3-D ISAR also uses the same interferometric approach as InSAR. The main difference is in geometry. Recent studies show that 3-D ISAR imaging is feasible [32], [33], [34], [35]. However, in most cases, the validation has been obtained by simulation [32], [33], or using huge targets, such as ship-borne targets [36] with relatively low resolution. To the authors' knowledge, there is no evidence of high-resolution 3-D ISAR imaging of noncooperative air targets based on real measurement. Such imaging is challenging and requires much more effort than in the simulated control environment, where the algorithm fully knows the target trajectory.
In recent years, several studies have emerged focusing on 3-D ISAR imaging. A common approach found in numerous publications involves deploying three receiving antennas arranged in two orthogonal baselines [32], [37], [38], [39]. This configuration facilitates interferometry in both directions, paving the way for a straightforward acquisition of 3-D imagery. Typically, 2-D imaging in these methodologies is achieved using the range–Doppler (RD) technique, which, while widely adopted, has inherent limitations concerning velocity and range resolutions. Several other methods for obtaining 3-D imagery have been proposed in literature, including the polar format algorithm (PFA), which the authors delve into in this work [40]. While some researchers have suggested employing just two receivers for 3-D imaging, the detailed mechanics of transforming the interferometric amplitude and phase data into 3-D images often remain inadequately elucidated [41], [42].
This article presents new results of developing the multichannel ground-based radar demonstrator allowing for high-resolution 3-D ISAR imaging of noncooperative air targets with a 15-cm resolution range. Contrary to approaches in literature, the proposed one uses only two receiving antennas for 3-D ISAR imaging. The system has been developed within the 3-D radar imaging for the noncooperative target recognition (RING) project. The RING project is a research and technological development project funded by the Italian and Polish Ministries of Defence and carried out for the European Defence Agency (EDA) in 2019–2023. The RING project focuses on developing and validating novel 3-D ISAR imaging techniques and novel noncooperative target recognition (NCTR) algorithms for this technology. The authors believe that the results of the RING project would be a game changer in the future of radar-based systems for target classification and recognition [43].
The main contribution of this article is the InISAR processing adopted for high-resolution noncooperative 3-D target imaging. The novelty can be summarized as follows.
The back-projection algorithm (BPA)-based approach was adopted for 3-D ISAR imaging using two receiving antennas.
The problem of trajectory estimation for high-resolution radars was addressed.
Extensive simulation experiments were carried out to confirm the method's usability.
Practical experiments, including the 3-D high-resolution imaging of noncooperative targets in a real-life scenario, were conducted.
The authors want to highlight that the whole article can be treated as a comprehensive tutorial guiding through principles, simulations, practical implementation, and measurement.
The rest of this article is organized as follows. Section II presents the theoretical background of 3-D ISAR imaging. In Section III, the authors present the simulation results of noncooperative targets' proposed 3-D high-resolution imaging. All the processing stages of the algorithm are explained step by step, showing the main challenges and solutions for correctly processing the data to obtain high-resolution and high-quality 3-D ISAR imaging of the noncooperative air targets. In addition, the challenges in signal processing for 3-D ISAR image creation of noncooperative targets with unknown trajectories are discussed in detail. In Section IV, the comparison to other 3-D imaging methods was presented. Then, Section V shows the real-life signal analysis results. In addition, the architecture of the developed high-resolution radar operating in the X-band and the first real-life results of the 3-D ISAR imaging of a noncooperative air target were obtained using records from the developed radar demonstrator. Finally, Section VI concludes this article.
SECTION II.
Theoretical Background
A. Signal Model
Range resolution (
For this study, the point reflectivity model was utilized for analysis. While the authors fully acknowledge its limitations and potential deviations from real-world scenarios, it is pertinent to note that this model offers a reasonable approximation under constrained integration times and operation in the far-field region. Therefore, given these specific conditions, the employment of the point reflectivity model is deemed appropriate for the presented research objectives.
One of the simplest ways to obtain a high-range resolution of SAR or ISAR systems is to use linear frequency-modulated (LFM) signal pulses. A single LFM pulse is defined as
Assuming stop-and-go approximation, the received echo signal reflected from
The use of the LFM waveforms allows for significantly reduced effective signal bandwidth. After the application of the dechirp method (matched filtering in the time domain), the received signal can be presented as
The model presented above (4)
works for the pulsed and continuous wave (CW) radars using LFM signals.
In the case of frequency-modulated continuous wave (FMCW) radar in the
model (2),
In the FMCW radar, according to (2), each moment can be assigned to the instantaneous frequency (beat signal) of the emitted signal. Therefore, by changing the coordinates in (4), it can be represented as follows:
The signal model given by (5) represents the cross-power spectrum density of the transmitted and received signals. It is worth noting that this form of the received signal does not consider the duration of a single pulse. This is simply due to the assumption that the scene is stationary for a single range profile evaluation.
B. Scene Geometry
Term
rk,1(tn) —Represents the position of a specific point with respect to the transmitter.r1(tn) —Denotes the position of the object's centroid with respect to the transmitter.rk,2,1(tn) —Represents the position of a specific point with respect to the first receiver.r2,1(tn) —Denotes the position of the object's centroid with respect to the first receiver.rk,2,2(tn) —Represents the position of a specific point with respect to the second receiver.r2,2(tn) —Denotes the position of the object's centroid with respect to the second receiver.rPk(tn) —Signifies the position of a particular point relative to the object's centroid.v(tn) —Represents the velocity of the object.
In
the presented model, the observed target moves in a straight line at an
established range from the radar at a fixed height. The target's
position in the global coordinate system is expressed by
Let
In
the case of determining radar imagery, it is important to determine how
the range of a given scattering point from the transmitting and
The object's orientation vector
The coordinate system will be associated with the center of mass of the observed target
C. 2-D High-Resolution ISAR Imaging
Over the years, many methods have been developed to determine 2-D SAR/ISAR images [44].
The most accurate methods with minor distortion are based on the BPA.
In general, it simulates the radar response of a given point with a
predetermined target trajectory. The simulation result correlates with
the registered signal to estimate the coefficient
The main disadvantage of the BPA [45],
which precludes its use in real time in practical applications, is the
number of calculations required to determine the final image. The
computational complexity of such an algorithm is
Substituting (9) and (6) into (5) and after rearranging terms, the signal received by the
This short method description does not consider any positioning or orientation errors and their influence on final results. Since the target trajectory is assumed to be known, it can easily be removed from the received signal
D. 3-D Projection Onto a 2-D Plane
Typically,
with SAR/ISAR processing, the generated image is 2-D. The imaging plane
can be chosen in any way, but the best results are obtained when the
plane is the same as the
The determined scattering coefficients correspond to the appropriate points on the plane for which the imaging is determined. It is worth noting that every scattering center of the observed target that does not lie on this plane will also be imaged. It is practically impossible to distinguish the image of a point located on the imaging plane from the image of a point below or above this plane when using data recorded with only one transmitter–receiver pair.
The point at which the image
of a scattering center not lying on the imaging plane will be located
depends on the relative position of the transmitting and receiving
antennas, the observed target, and its direction of movement. Of course,
due to the changing geometry of the scene, for a sufficiently long
integration time, points not lying on the imaging plane will not be
focused. However, relatively short integration times are used for a
wideband radar with a high carrier frequency. Therefore, it can be
assumed that the scene's geometry does not change so much that the
images of points not lying on the
Two points will be identical on the image if they have the same bistatic parameters. Relative to the target center, the bistatic range can be defined as
In this context, the parameter
Let
Generally, the position
E. Interferometry-Based 3-D Imaging Technique
One way to achieve 3-D imaging is to use interferometry. This method is generally based on information about the phase of the estimated scattering coefficient of the imaged target's point.
If the antenna array of the radar system is calibrated, the phase of the received signal should not change during the imaging procedure. When a reflecting point has a real-value reflectivity value, the estimated reflectivity value of the scattering center should also be a real-value number. However, this statement only holds if the scattering center is located precisely on the grid, at the position where the value is determined. Therefore, the estimated single scattering point reflectivity may have shifted phase in complex value reflectivity. The phase change of the determined value depends on the wavelength of the signal used to illuminate the target and the difference in the distance between the actual position of the point image and the grid point representing the given point.
In the case of the interferometry
technique, the fact is that for two receiving antennas located at
different heights, the projection position of a given point on the
imaging plane will be different. This results directly from (16).
With a slight difference in the position of the antennas, it can be
assumed that the difference in the position of the projected point
The range expressed by (13) denotes the bistatic5
range of a given scattering center in relation to the bistatic range of
the target's center. In this expression, the compensation of the range
of the target from the radar is considered, which ensures that it has no
direct effect on the image formation process. The value given by this
expression is the length of the vector, being the projection of the
vector
Combining (16) and (18) into a single equation system, the following expression can be stated
F. 3-D Reconstruction Analysis
In 3-D ISAR imaging, the solution vector
The invertibility of matrix
For matrix
A detailed analysis of (19)
and the precision of determining the 3-D point's location exceeds the
scope of this article. Here, the authors merely wish to highlight
situations where matrix
Since
interferometry is not fully 3-D imaging, additional assumptions about
the nature of the target are necessary. First, there cannot be two
points with the same projection onto the imaging plane. Otherwise, those
two points will interfere, and the estimated phases
SECTION III.
3-D Imaging Verification via Simulations
Many simulations were conducted to verify the mechanism for determining the 3-D imagery described in Section II. A block diagram presented in Fig. 2 shows the verification procedure for a single azimuth angle. Initially, the direction of the object's motion was selected. Subsequently, the target trajectory was generated, and a simulation of the object's echo was conducted. In the following stages, a 2-D image was created, interferometry was determined, and a 3-D reconstruction of the simulated object was carried out. The final step involved comparing the estimated positions of the object's points with those simulated. Representative results are presented in the next section.
A. Simulation Setting
A simplified model of the KR-03 Puchatek glider consisting of 117 points was used. The model can be seen in Fig. 3. The simulated target is similar to that used in the real-life experiment described in detail in Section V. The simulated object was moving
B. Range–Doppler Map Evaluation
To verify the performed simulations, RD maps were evaluated. Fig. 5 is a reference for other images for better intuition and understanding of the imaged target and scenario. It shows the difference between the RD and the considered techniques.
Fig. 5.
RD maps for two time instants (integration time was
RD imaging is numerically thrifty; no input parameters, like trajectory, are required. As can be seen, the glider shape can be distinguished in the picture; however, the quality is low, and the image is tilted. Based on RD imaging, 3-D reconstruction might need to be more precise. More complex imaging algorithms are recommended for high-resolution imaging.
C. 2-D Imaging
In Fig. 6, a 2-D ISAR image obtained using the PFA algorithm can be seen. The scatterers can be distinguished due to much higher imaging resolution compared to Fig. 5. For example, the image contrast of results presented in Fig. 6 equals 3.48 versus 1.61 and 1.85 of images shown in Fig. 5(a) and (b), respectively. However, it is impossible to obtain information about the elevation profile. It is worth noting that, in this case, the tail wing above the imaging plane is shifted in the positive direction of the OY axis. This shift results from the simple fact that elements above the imaging plane are slightly more distant from the radar than corresponding elements on this particular plane in the simulated scenario. Fortunately, this shift does not noticeably blur these points in the image, and almost all scattering centers can be identified.
D. Interferometry and 3-D Imaging
The phase difference, shown in Fig. 7,
was determined based on complex 2-D imaging values for different
receivers. The color indicates the value of the phase of the estimated
scattering coefficient whose amplitude, shown in Fig. 6, is greater than
The graph presented in Fig. 7 is not a typical 3-D image, but on its basis, it is possible to determine the altitude profile of the observed target. It is worth paying particular attention to the phase value of the points in the fuselage area. The darker areas, corresponding to lower points, are shifted in the negative y-axis direction. On the other hand, the brighter ones, corresponding to higher points, are shifted toward the positive values of the OY axis. Nevertheless, in the adopted model, shown in Fig. 3, all hull points have the y coordinate equal to 0. Similarly to the shift described in Section III-C, this results from the different ranges of those areas from the transmitting and receiving antennas and is the basis of the 3-D interferometric imaging technique.
Finally, the 3-D ISAR imaging described in Section II is conducted. Fig. 8 shows the result. In the 3-D image, points making the glider can be distinguished and presented as blue circles. The radius of the circle corresponds to the amplitude of the scattering point.
E. Simulation Conclusions
The
results presented in this section prove that the proposed methods work
correctly. 3-D interferometric images can be obtained with sufficient
quality. Fig. 8 presents the 3-D target reconstruction. The
average distance of the reconstructed target's estimated points from the
points of the simulated model is not more than
In addition, simulations were carried out for different directions of the target's motion relative to the LOS. Fig. 9
shows the average distance of all estimated points of the reconstructed
target from the points of the simulated model as a function of the
target's azimuth. The lowest values are obtained when the target moves
in the direction perpendicular to the LOS. This direction in the
simulation corresponds to an azimuth of
What is important to note is that this data processing approach works well on simulated data, where an exact trajectory can be used. Additional procedures that prepare and process data must be used to process real-world data. Implementing those procedures and finding adequate algorithms is one of the main difficulties in 3-D ISAR interferometric imaging. Those procedures, problems, and mitigations are described in the next section.
SECTION IV.
Comparison to Other Methods
In 3-D ISAR imaging, existing techniques often rely on the RD algorithm, which typically requires at least three receiving antennas to accurately reconstruct a 3-D image of a moving target. However, the proposed method offers a significant advantage: it can generate high-quality 3-D images with only two receiving antennas, which reduces system complexity, dimensions, costs, and weight. By requiring fewer receiving antennas, the proposed method offers potential cost savings. It simplifies the imaging setup, making it more accessible for various applications and easy to deploy in demanding locations.
While ISAR imaging is a well-established method for generating high-resolution 3-D images of moving targets, many existing techniques rely on the CLEAN algorithm to separate the target from the clutter in the resulting image. However, this approach can be computationally intensive and limit the imaging process's speed and efficiency. In contrast, the proposed method simultaneously processes the pixels of the entire image, which offers several benefits. The presented technique reduces the computational complexity by analyzing the entire image in one step. It speeds up the imaging process, making it more efficient and practical for real-world applications. Furthermore, the proposed approach avoids the limitations of traditional CLEAN-based techniques, which can struggle to reconstruct targets with complex shapes accurately or in scenarios with significant interference.
The 3-D target reconstruction results obtained using the CLEAN technique are presented in Fig. 10. The reconstructed target model generally fits well with the target model used in the simulation, and the number of scatterers is estimated accurately with this method. However, it is important to note that the CLEAN technique is computationally intensive, requiring more than 100 evaluations of the imaging and simulating processes to generate the final image.
While the CLEAN technique is a powerful tool for ISAR imaging, it has some limitations, mainly when dealing with dense reflectivity functions. The problem arises when the target contains complex features or is located in an environment with high interference levels, leading to a dense reflectivity function.
It is essential to clarify that the presented analysis does not explicitly enumerate the required computational operations, as this is inherently contingent upon the selected imaging methodology. In this study, the authors advocate for the PFA method, renowned for its computational efficiency in image derivation. It is noteworthy, however, that alternative strategies, such as the classic back-projection, are equally viable. The discourse primarily underscores the merit of processing the complete 3-D image in a consolidated step. This stands in contrast to iterative techniques like CLEAN, which tend to extract individual reflecting points repetitively. From the presented analysis, this comprehensive approach to image processing provides a more integrated and holistic representation, surpassing the granularity offered by conventional point extraction methodologies.
SECTION V.
Real Data Measurement Description
Section III outlined the signal processing chain using simulated data. It should be noted that processing real-life signals is significantly more challenging than simulated data. This is mainly due to the adopted models of physical phenomena and the assumption of ideal conditions.
This
section presents the processing of signals recorded during experiments
with a real target. Particular attention was paid to the aspects
affecting the final result's quality. These issues include, first of
all, the estimation of the trajectory and spatial orientation of the
observed target. Generally, the relative accuracy of the range evaluated
should be lower than the fraction on wavelength, which in the case of
X-band radar is less than
Fig. 11 presents a block diagram of the processing algorithm adapted to measurement data. An essential part of the presented algorithm is classical radar processing, which leads to detecting and tracking the observed target. Thanks to this, it is possible to extract the desired target echo from the recorded signals and process it following the procedure presented in Sections II and III.
A. FMCW Radar Demonstrator
An
FMCW radar with one transmitting and four receiving channels was used
during the measurement campaign. An example of an antenna array of the
X-band system is presented in Fig. 12. The horn antennas used during the experiment cover the frequency band from
During the measurement campaign, the system could register echo signals for up to four antennas, and all data recorded were processed. However, in obtaining 3-D imaging, only data from two of those antennas were used. This approach is consistent with the initial proposition, underscoring the core methodology.
B. Measurement Campaign and Data Acquisition
The observed target was a KR-03 Puchatek glider shown in Fig. 13. It was on its final approach for landing. The target was moving at constant forward and vertical speeds.
The
Puchatek glider used for method validation is relatively big compared
to general aviation aircraft and is mainly made of metal, which provides
good SNR. The Puchatek has a wingspan of
C. Signal Conditioning and Clutter Filtering
The method presented in Section II is based on the assumption that the signal is transmitted and received at the antennas' points. In a real-world scenario, the analog front end (AFE) induces additional delays and distortions that must be compensated. In the presented work, this process, called signal conditioning, is based on estimating the parameters of the first echo caused by antenna leakage.
After signal conditioning, strong echoes of stationary objects are removed by low-pass filtering. The finite impulse response (FIR) filter with a sufficiently long pulse response allows one, on the one hand, to keep the echo of the target close to zero-Doppler; on the other hand, it removes most of the stationary echoes. As a result of signal conditioning and clutter removal, the SNR increases, and the target can be detected.
D. RD Processing
Relatively
high target speeds usually create two serious problems that must be
addressed. The first problem is range migration directly caused by the
significant velocity. In the case of radars with
E. Target Detection and RD Positioning
Before imaging, a noncooperative air target must be detected and tracked first. One of the main challenges of high-resolution radars is precise positioning, which is necessary for ISAR imaging. Assuming a high SNR, the expected accuracy of determining the target's range and velocity should be similar to the resolution of the RD image. Air target positioning with high-resolution radars has not been widely discussed in literature and has yet to be comprehensively resolved.
The adopted algorithm for target position estimation consists of several stages. First, based on evaluated RD maps, the standard constant false alarm rate (CFAR) is applied, and points above the threshold are returned. Then, density-based spatial clustering of applications with noise (DBSCAN) [47] combines a dozen detections into several potential targets.
The actual target range and velocity are estimated by having detections clustered. This results from several observations. At any time, the target is visible from a slightly different angle. Therefore, at each subsequent moment, the echoes of various elements of the observed target may dominate the recorded signal, and the classic detection algorithm may return other points. Moreover, the registered echo might be incomplete, which biases the target position's estimation.
The
method based on the RD target image's center of gravity was adopted
according to the abovementioned difficulties. The target's location
Fig. 14 shows two extracted echoes of the observed target on the RD maps evaluated for two different moments, together with marked centers of gravity. It is worth noting that there are significant differences in the echo structure, which impedes the proper estimation of the target's center.
F. RD Tracking
Target tracking in radial coordinates is determined in successive moments based on the estimated RD positions. Based on these track parameters, it is possible to decide how the range and radial velocity change over time. Due to the limited possibilities of accurately estimating track parameters, it is essential to estimate the motion model correctly. In this case, the Kalman filter is usually applied and adopted.
Fig. 15 shows the result of radial tracking for individual receiving antennas in different colors. A relatively high variance of the parameters of the estimated tracks can be noticed. The estimated trajectory in this way is unsuitable for evaluating the target position and must be corrected in the next steps.
G. Target Extraction
Other echoes of moving targets and noise or interference affect the final processing results. This influence manifests itself primarily in a significantly reduced SNR. Thus, the next critical signal processing stage is extracting the observed target echo from the recorded data.
The trajectory estimated during RD tracking isolates the target echo. The input data are filtered with a 2-D nonstationary bandpass filter. Since the received signal contains only the echo of the observed object, it is possible to significantly reduce the sampling frequency, both in the fast-time and slow-time domains, which additionally reduces computational complexity.
Fig. 16 presents range-slow time maps for extracted target echo. With the red line, the estimated target center is denoted. Based on estimated ranges, accurate target tracking and positioning are further performed.
H. Cartesian Tracking
Accurate location and target tracking were among the most challenging stages of data processing. The quality of the final result heavily depends on the accuracy of the estimated trajectory. It is important to note that an object with an incorrectly matched 3-D trajectory will likely have a distorted representation. In the case of aerial objects, such as the observed gliders, symmetry is expected. However, this symmetry can be disrupted if the azimuth and trajectory are estimated incorrectly, leading to skewed or unbalanced images.
During the measurements, the antenna array of four antennas was placed at the corners of a rectangle with a side length of 2 m (see Fig. 12). Despite this setup, determining the elevation and azimuth angles of the target with high precision was challenging. Consequently, it was assumed that the observed target, a landing glider, moved in a straight line at a constant velocity. Given the low altitude typically associated with landing gliders, it was further assumed that the target was at a relatively low height. Based on these assumptions, it was determined the target's position in the Cartesian coordinate system using only range measurements.
This approach, centered on simplicity, proved effective for initial trajectory estimation in our experimental setup. The linear motion assumption provided a practical basis for the presented analysis, especially when detailed motion dynamics were either unavailable or unnecessary for the level of imaging the authors sought to achieve. While this method may not capture the complete range of motion dynamics, it offers a foundational understanding of the target's trajectory, sufficient for imaging purposes.
Furthermore, the iterative refinement of observation angles, based on initial position estimates and the assumed linear trajectory, allowed for incrementally improving the accuracy of target tracking. This method, grounded in both the initial assumptions and the data collected during the experiment, demonstrates the adaptability of the presented approach to different scenarios, even those with limited prior information about the target's movement. The ability to adjust for and correct potential distortions due to incorrect trajectory estimates further enhances the utility and applicability of the proposed method in practical situations.
I. ISAR Imaging
When the recorded data were preprocessed and the target's trajectory determined, the 2-D imaging was performed using the PFA method described in Section II. The processing results are similar for all receiving antennas placed at different heights. Fig. 17 presents the result for a single channel. The images were sufficiently focused and did not require an additional automatic focusing approach. It is worth noting that the imaged target is slightly shifted to the left. This shifting is due to the incorrectly estimated initial position of the target. However, this positioning offset of the images does not affect the result's quality.
J. Interferometry and 3-D Imaging
The last signal processing stage is to perform 3-D imaging of the observed target. The third dimension is obtained from the phase differences of the estimated reflectance coefficients. Depending on the antenna's position, these values will vary; thus, getting information about the third dimension is possible according to the procedure outlined in Section II.
The phase noise filtering for the obtained images is essential to the procedure. These speckle noises significantly affect the quality of the acquired 3-D point cloud. Therefore, the median filtering procedure is performed before comparing both ISAR images. In this way, most of the phase noise is removed, and the accuracy of estimating the height of individual image points is significantly better.
Fig. 18 presents the result of
comparing the phases of the reflectance coefficients from the two ISAR
images. It is evident from the diagram that the profile is notably
smooth. Specifically, the interferometric phase remains within a
The PZL KR-03 Puchatek has very distinctive wings moving up toward its end tips, which can be seen in the photo in Fig. 13. The exact shape can be seen on the interferometric height profile in Fig. 19. This proves the method's quality and accuracy in representing 3-D shapes and their resolution on the vertical axis. Images obtained using measurement data differ slightly from those obtained through simulation. This occurs because the simulation does not account for changes in reflectivity and the propagation of RF waves. Even though the trajectory is well fitted, it differs from the real one. However, even with these inconveniences, the image shows that the features of the PZL KR-03 Puchatek air target can be obtained with accuracy.
This article has shown a detailed method of practical 3-D ISAR imaging. Theoretical analysis, numerical examples, and real-life signal processing has supported the work. The presented results prove that the system is capable of high-resolution 3-D ISAR imaging of noncooperative airborne targets in a real-world scenario. The imaging results are consistent with expectations: the obtained 3-D image resembles the image created with simulated data. Observed discrepancies are partially caused by minor misalignment of a projection plane. The similarity between images is promising regarding the future NCTR system application.
The PFA method used combines good time complexity and decent imaging quality. The results prove that the back-projection-based algorithms are well fitted to 3-D ISAR imaging. This method needs a high-quality trajectory to remove the translational part of the target. The benefit of using such a group of algorithms is direct dimensioning, both in the 2-D imaging plane and the 3-D height profile. In addition, the presented technique uses two receiving antennas instead of three, as typical methods in literature do. Therefore, aside from reducing computational complexity, the receiver cost of the 3-D ISAR imaging radar is 33% lower due to removing one channel.
It is worth noting that the target's position in 3-D space is also necessary to estimate its spatial orientation. While it is possible to determine the location based on the distance and direction measurements of the received echo, the estimation of spatial orientation has not been described in literature. This aspect requires further research. There are indications that this type of data cannot be unambiguously reproduced in the case of monostatic radar. Therefore, additional assumptions are necessary. Typically, the target is assumed to be oriented along the trajectory it is moving. This assumption is valid in many cases, especially if the target moves straight. Nevertheless, the assumption that the target moves in a straight line, typically stated for short integration time and used in previous processing data, is no longer valid for more extended target trajectories. This is one of the most challenging parts of high-resolution radar signal processing.
Due to the trajectory estimation and autofocus, the projection plane misalignment between observation and simulation is expected to be limited. Model-based classification can be compensated using algorithms presented in [33]. Plans for the future include the assessment of NCTR algorithms using a representative measurement dataset and developing 3-D ISAR-oriented NCTR algorithms. Up to this moment, literature regarding 3-D ISAR image classification is limited: papers available are often recent and describe NCTR-related data preprocessing [33] or classification of simulated 3-D ISAR data [48]. Multiple articles regarding 3-D object recognition are available for other sensor types like LIDAR [49], [50], [51], [52], infrared [53], [54], and computer vision [55], [56], [57]. 3-D ISAR imaging also has the potential to deliver data of high interpretability, increasing the ISAR's capabilities regarding reconnaissance and surveillance.

Fig. 2.
Block diagram of presented 3-D ISAR processing verification method.

Fig. 5.
RD maps for two time instants (integration time was

Fig. 6.
ISAR image of the simulated target for the PFA algorithm.

Fig. 7.
Phase shift for interferometric measurements.

Fig. 8.
Comparison of reconstructed target and the simulated one.

Fig. 9.
Reconstruction performance in function of target moving direction.
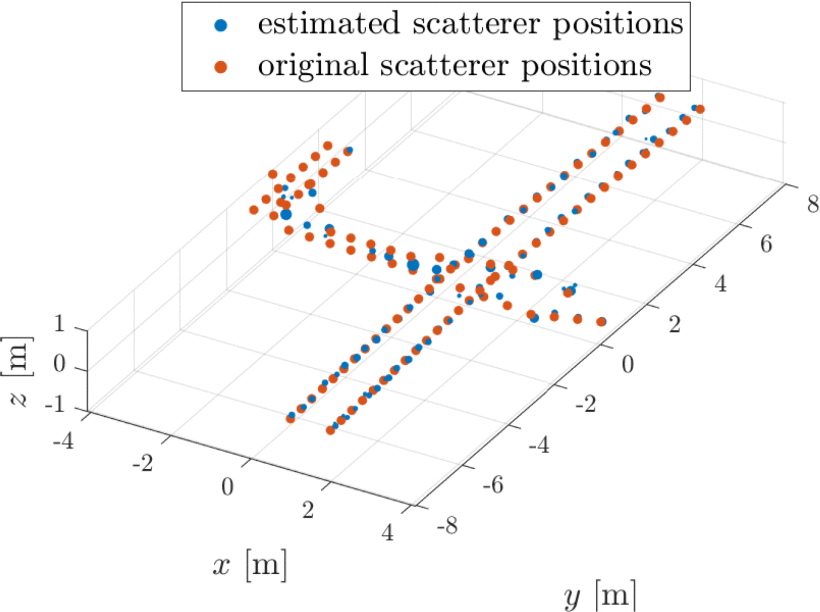
Fig. 10.
comparison of reconstructed target and the simulated one for CLEAN technique.

Fig. 12.
Antennas setup of the X-band active radar demonstrator.

Fig. 14.
Detection on RD maps (integration time -

Fig. 16.
RT map with a superimposed trajectory (red curve).

Fig. 18.
Interferometric phase of ISAR images of the PZL KR-03 Puchatek.



























No comments:
Post a Comment