Multistatic-Radar RCS-Signature Recognition of Aerial Vehicles: A Bayesian Fusion Approach

RATR block diagram.
Multiple radars continuously track and pulse an EMW at a moving UAV target.
The each individual radar’s belief about the UAV type is at time step $t$ is fused
in an Bayesian way and used to update recursively a posterior belief about the UAV type.

 

Multistatic-Radar RCS-Signature Recognition of Aerial Vehicles: A Bayesian Fusion Approach

Michael Potter Northeastern University, Boston, MA 02115, USA  

Murat Akcakaya University of Pittsburgh, Pittsburgh, PA 15260, USA  

Marius Necsoiu DEVCOM ARL, San Antonio, TX 78204, USA 

Gunar Schirner Northeastern University, Boston, MA 02115, USA  

Deniz Erdoğmuş Northeastern University, Boston, MA 02115, USA Tales Imbiriba Northeastern University, Boston, MA 02115, USA

Electrical Engineering and Systems Science > Signal Processing

[Submitted on 28 Feb 2024]

Michael Potter, Murat Akcakaya, Marius Necsoiu, Gunar Schirner, Deniz Erdogmus, Tales Imbiriba

Radar Automated Target Recognition (RATR) for Unmanned Aerial Vehicles (UAVs) involves transmitting Electromagnetic Waves (EMWs) and performing target type recognition on the received radar echo, crucial for defense and aerospace applications. Previous studies highlighted the advantages of multistatic radar configurations over monostatic ones in RATR.

However, fusion methods in multistatic radar configurations often suboptimally combine classification vectors from individual radars probabilistically. To address this, we propose a fully Bayesian RATR framework employing Optimal Bayesian Fusion (OBF) to aggregate classification probability vectors from multiple radars. OBF, based on expected 0-1 loss, updates a Recursive Bayesian Classification (RBC) posterior distribution for target UAV type, conditioned on historical observations across multiple time steps.

We evaluate the approach using simulated random walk trajectories for seven drones, correlating target aspect angles to Radar Cross Section (RCS) measurements in an anechoic chamber. Comparing against single radar Automated Target Recognition (ATR) systems and suboptimal fusion methods, our empirical results demonstrate that the OBF method integrated with RBC significantly enhances classification accuracy compared to other fusion methods and single radar configurations.

Comments:	To be submitted to IEEE Transactions on Aerospace and Electronic Systems
Subjects:	Signal Processing (eess.SP); Computer Vision and Pattern Recognition (cs.CV); Machine Learning (cs.LG); Probability (math.PR); Machine Learning (stat.ML)
Cite as:	arXiv:2402.17987 [eess.SP]
	(or arXiv:2402.17987v1 [eess.SP] for this version)
	https://doi.org/10.48550/arXiv.2402.17987

Submission history

From: Michael Potter [view email]
[v1] Wed, 28 Feb 2024 02:11:47 UTC (4,323 KB)

arxiv.org

Multistatic-Radar RCS-Signature Recognition of Aerial Vehicles: A Bayesian Fusion Approach

Michael Potter Northeastern University, Boston, MA 02115, USA

Research was sponsored by the Army Research Laboratory and was accomplished under Cooperative Agreement Number W911NF-23-2-0014. The views and conclusions contained in this document are those of the authors and should not be interpreted as representing the official policies, either expressed or implied, of the Army Research Laboratory or the U.S. Government. The U.S. Government is authorized to reproduce and distribute reprints for Government purposes notwithstanding any copyright notation herein.

{IEEEkeywords}

Radar Cross Section, Bayesian Fusion, Unmanned Aerial Vehicles, Machine Learning

1 INTRODUCTION

Radar Automated Target Recognition (RATR) technology has revolutionized the domain of target recognition across space, ground, air, and sea-surface targets [1]. Radar advancements have facilitated the extraction of detailed target feature information, including High Range Resolution Profile (HRRP), Synthetic Aperture Radar (SAR), Inverse Synthetic Aperature Radar (ISAR), Radar Cross Section (RCS) and Micro-Doppler frequency [2]. These features have enabled Machine Learning (ML) and Deep Learning (DL) models to outperform traditional hand-crafted target recognition frameworks [1, 3]. Furthermore, RATR seamlessly integrates with various downstream defense applications such as weapon localization, ballistic missile defense, air surveillance, ground and area surveillance among others [4]. While RATR is applied to various target types, our focus will center on the recognition of Unmanned Aerial Vehicles (UAVs). Henceforth, the terms UAVs and drones will be used interchangeably.

UAVs are a class of aircraft that do not carry a human operator and fly autonomously or are piloted remotely [5]. Historically, UAVs were designed solely for military applications such as surveillance and reconnaissance, target acquisition, search and rescue, and force protection [6, 7]. Recently we have entered the ”Drone Age [8], aka personal glsuav area; where there has been a rapid increase in civilian UAV use for cinematography, tourism, commercial ads, real estate surveying and hot-spot / communications [9, 10].

However, the potential misuse of UAVs poses significant security and safety threats, which is prompting governmental and law enforcement agencies to implement regulations and countermeasures [11, 12]. Adversaries may transport communication jammers with UAVs [13], perform cyber-physical attacks on UAVs (possibly with kill-switches)[14], or conduct espionage via video streaming from UAVs [15]. Criminals may perform drug smuggling, extortion(with captured footage), and cyber attacks (on short-range Wi-Fi, Bluetooth, and other wireless devices) [10]. These security and safety issues are exacerbated by the increased presence of unauthorized and unregistered UAVs [16]. The growing concerns of the new Drone Age, coupled with the increasing nefarious use of UAVs [17], necessitates robust, accurate, and fast RATR frameworks.

Radar systems transmitElectromagnetic Waves (EMWs) directed at a target, and receiving the reflected EMWs (aka radar echoes) [18]. Radar systems are ubiquitous in Automated Target Recognition (ATR) because of the long-range detection capability, ability to penetrate obstacles such as atmospheric conditions, and versatility in capturing detailed target features [18]. Popular radar-based methods of generating target features are ISAR, Micro-Doppler signature, and RCS signatures. ISAR generates high resolution radar images by using the Fourier transform and explotation of the relative motion of the target UAV to create a larger “synthetic” aperture [19]. However, ISAR images degrade significantly when the target UAV has complex motion, such as non-uniform pitching, rolling, and yawing [20]. Micro-Doppler signatures are the frequency modulations around the main Doppler shift due to the UAV containing small parts with additional micro-motions, such as the blade propellers of a drone [21]. However, Micro-Doppler signatures may vanish due to the relative orientation of the drone. Both ISAR and Micro-Doppler require high radar bandwidth for processing and generating target profiles, which is computationally expensive [22, 23]. The RCS of a UAV, measured in dB m² and proportionate to the received power at the radar, signifies the theoretical area that intercepts incident power; if this incident power were scattered isotropically, then it would produce an echo power at the radar equivalent to that of the actual UAV [24]. RCS signatures have low transmit power requirements, low bandwidth requirements, low memory footprint, and low computational complexity [25, 20]. For these reasons, much of the literature focuses on RCS data collected from transmitted signals with varying carrier frequencies.

Most of the UAV ATR literature using RCS signatures focuses on monostatic radar configurations and does not utilize multiple individual monostatic radar observations at a single time step. However, there are common multistatic radar configuration fusion rules which are based on domain-expert knowledge. The SELection of tX and rX (SELX) fusion rule [26, 27] combines the classification probability vectors from each radar channel via a weighted linear combination, where the weights are higher for the channels with the best range resolution and high Signal-to-Noise-Ratio (SNR). The common SNR fusion rule [28] also combines the classification probability vectors for each radar channel via a weighted linear combination, but the weights proportional to the SNR (higher SNR leads to larger weight). Other works employ heuristic soft-voting, which averages the probability vectors from each radar [29]. However, domain expert’s heuristics may be influenced by cognitive bias or limited by subjective interpretation of experts [30, 31], leading to incorrect conclusions. Furthermore, Bayesian decision rules are known to be optimal decision-making strategies under uncertainty, compared to domain-expert’s heuristic-based decisions [32, 33].

Our Contributions of this work: To the best of our knowledge, this work is the first to provide a fully Bayesian RATR framework for UAV type classification from RCS time series data. We employ an Optimal Bayesian Fusion (OBF) method, which is the Bayesian fusion method for optimal decisions with respect to 0-1 loss, to formulate a posterior distribution from multiple individual radar observations at a given time step. This optimal method is then used to update a separate Recursive Bayesian Classification (RBC) posterior distribution on the target UAV type, conditioned on all historical observations from multiple radars over time.

Thus, our approach facilitates efficient use of training data, informed classification decisions based on Bayesian principles, and enhanced robustness against increased uncertainty. Our method demonstrates a notable improvement in classification accuracy, with relative percentage increases of 35.71% and 14.14% at an SNR of 0 dB compared to single radar and RBC with soft-voting methods, respectively. Moreover, our method achieves a desired classification accuracy (or correct individual prediction) in a shorter dwell time compared to single radar and RBC with soft-voting methods

The paper is structured as follows: Section II describes the related work for RATR on RCS data; Section III details the data, data simulation and dataset structure; Section IV explains the OBF method and RBC for our RATR framework; Section V discusses the experiment configuration and results; Section VI derives conclusions on our findings.

2 RELATED WORK

We sort the literature on RATR target recognition models into two types: statistical ML and DL.

Statistical ML: Many methods leverage generative probabilistic models using Bayes Theorem to classify a target UAV based on the highest class conditional likelihood [34, 20, 35]. The method in [34, 20] classified commercial drones with generative models such as Swerling (1-4), Gamma, Gaussian Mixture Model (GMM) and Naive Bayes on multiple independent RCS observations simulated from an monostatic radar in an anechoic chamber. However, there could potentially exist a hidden temporal relationship among the RCS observations. In the study of [36], unspecified aircrafts were classified based on RCS time series data using an Hidden Markov Model (HMM) fitted with the Viterbi algorithm. In this model, the hidden state represented the contiguous angular sector of the UAV-radar orientation, with the observations comprising RCS measurements. While generative models are designed to capture the joint distribution of both data and class labels, this approach proves computationally inefficient and overly demanding on data when our primary goal is solely to make classification decisions [37].

Figure 1: M100 HH polarization RCS signature images from the Indoor Near Field experiments from [38]

Discriminative ML models directly find the posterior probability on the UAV type given RCS data, and have been used in RATR for UAV type classification [34, 39, 40, 41]. The study described in [41] employed summary statistics of RCS time series data to classify between UAV and non-UAV tracks, utilizing both Multi Layer Perceptron (MLP) and Support Vector Machine (SVM) models. However, Ezuma et al showed that Tree-based classifiers outperformed generative, other discriminative ML models (such as SVM, K - Nearest Neighbors (KNN), and ensembles), and deep learning models [34]. Furthermore, [42] showed Random Forests significantly outperform SVM when classifying commercial drones using micro-Doppler signatures derived from simulated RCS time series data [40]. While these methods demonstrate high classification accuracy in monostatic radar experiments, they do not take advantage of or account for multistatic radar configurations. Instead of consolidating all the features from multiple RCS observations into a large input space, it is more effective to construct individual models for each time slice or radar viewpoint [37]. We now shift our focus to DL methods, acknowledging the undeniable ascent of DL [43, 44].

DL: The enhanced capability of radar to extract complex target features has sparked an increasing demand for models capable of using complex data, exemplified by the rising use of DL model [28, 1]. The work in [45] was the first application of Convolutional Neural Network (CNN) for monostatic radar classification based on simulated RCS time series data of geometric shapes. However, CNNs do not incorporate long-term temporal dynamics into their modeling approach. To address this limitation and capture long-term and short term temporal dynamics, many studies have used Recurrent Neural Networks (RNNs) and Long Short Term Memorys (LSTMs) networks [46]. These works classify a sliding time window or the entire trajectory of RCS time series data corresponding to monostatic radars tracking an UAV [47, 48, 49]. [50] combined a bidirectional Gated Recurrent Unit (GRU) RNN and a CNN to extract features from RCS time series data of geometric shapes and small-sized planes, subsequently using an Feed Forward Neural Network (FFNN) for classification. Lastly, [29] employed a spatio-temporal-frequency Graph Neural Network (GNN) with RNN aggregation to classify two simulated aircraft with different micromotions tracked by a synthetic heterogeneous distributed radar system. While numerous DL approaches have been utilized in RCS based RATR classification frameworks, challenges still persist, including the necessity for substantial data to generalize to unseen data [51], overconfident predictions [52], and a lack of interpretability [53]. Furthermore, Ezuma et al showed that Tree-based ML models outperformed traditional deep complex Neural Network (NN) architectures for commercial drone classification. Thus this paper focuses on the following ML models: Extreme Gradient Boosting (XGBoost), MLP with three hidden layers, and logistic regression.

3 Multi-Static RCS Dataset Generation

This section outlines the process of mapping simulated azimuth and elevation angles to RCS data measured in an anechoic chamber. This involves calculating the target UAV aspect angles (azimuth and elevation) relative to the Radar Line Of Sight (RLOS) while considering the target UAV pose (yaw $\gamma$, pitch $\alpha$, roll $\beta$ and translation $T$). The pose of the target UAV will change over time as a function of a random walk kinematic model.

Figure 2: Indoor Near Field RCS signature collection utilizing different polarization combinations of EMW signals transmitted and received from from quasi-monstatistc radar.

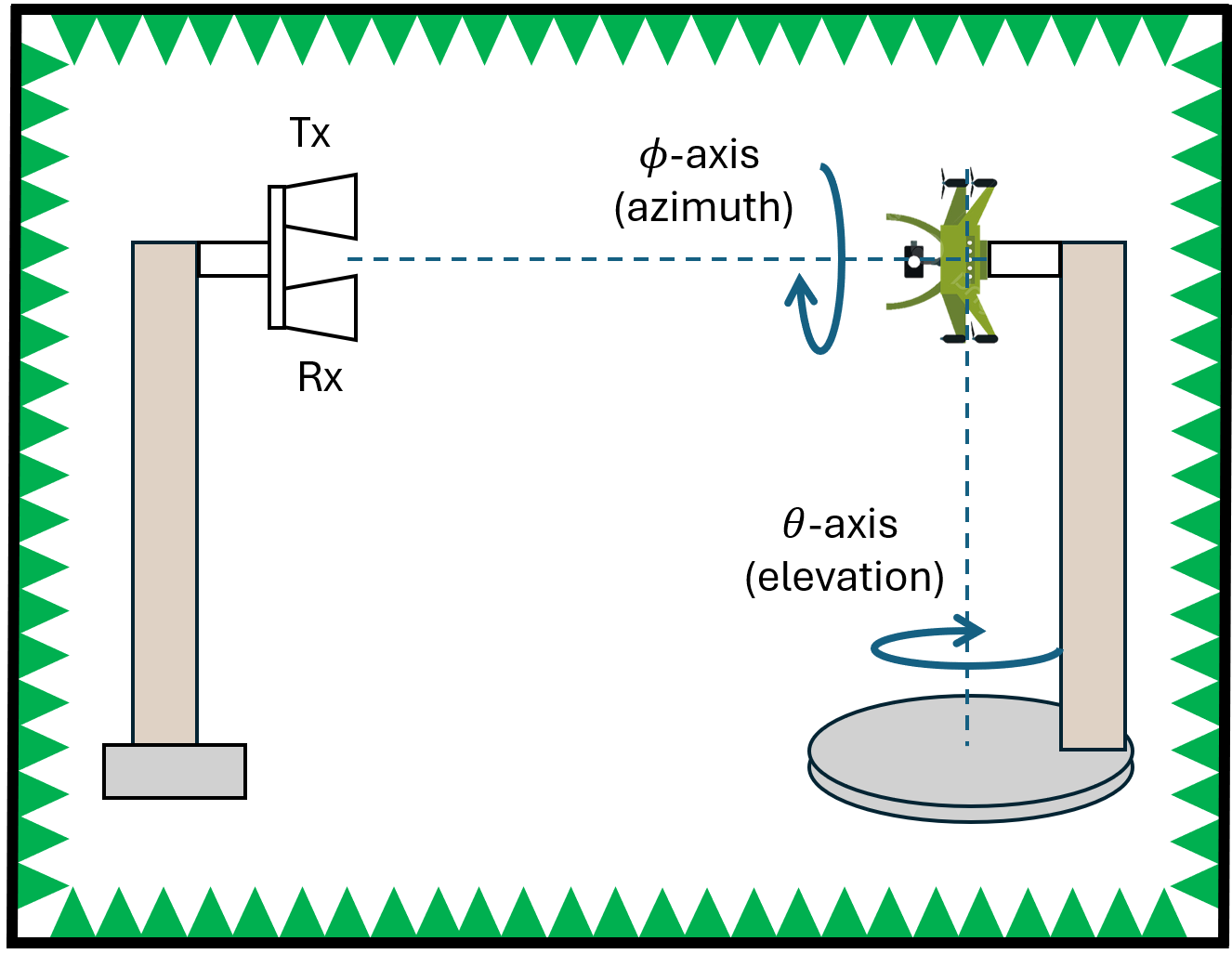
3.1 Existing Data

We analyze the approximate RCS signatures of 7 different UAVs collected in [38]: the F450, Heli, Hexa, M100, P4P, Walkera, and Y600 . The data was collected in an anechoic chamber, where a quasi-monostatic radar transmitted EMWs at $F=15$ frequencies (26-40 GHz in 1 GHz steps) while stepped motors rotated the UAV around the azimuth axis ($\varphi$ in Figure 2) and the elevation axis ($\theta$ in Figure 2) [38]. The azimuth spans from 0 to 180 degrees, while the elevation extends from -95 to 95 degrees, both in 1-degree increments. An example of the RCS image of a UAV from [38] is shown in Figure 1. We leverage the real RCS signatures to create training and testing datasets corresponding to simulated/synthetic radar locations and drone trajectories.

3.2 Training Data Generation

We sample azimuth and elevation uniformly at random, where the spread is bounded by each drone’s minimum and maximum aspect angles from the experimental setup in [38]. The azimuth and elevation samples, $\varphi$ and $\theta$ respectively, are mapped to a measured RCS signature $\sigma \in {ℛ}^F$ from [38], where we linearly interpolate the mapped RCS measurements for continuous azimuth and elevations not collected in [38]. For each UAV type $c\in {𝒞}_{train}=[1,\mathrm{\dots },7]$, we generate $N_{train}$ samples such that $|{𝒟}_{train}|=|{𝒞}_{train}|N_{train}$. Training a discriminative ML classifier under the perspective of a single radar at a single time point enables efficient sampling and training. Generating training data for multistatic radar configurations would deal with the curse of dimensionality, where trajectories (a sample trajectory being multiple time points concatenated) compounded with multiple radars would exponentially increase the required number of samples to adequately cover the input space. In summary, the training dataset ${𝒟}_{train}$ has the following structure:

${𝒟}_{train}={\{(x_i,c_i)\}}_{i=1}^{N_{train}}$

(1)

where $x_i^{(t)}=[{\sigma }_i^{(t)},{\varphi }_i^{(t)},{\theta }_i^{(t)}]$ contains the noisy RCS signature, the noisy azimuth and the noisy elevation. The noisy RCS signature, azimuth, and elevation will be discussed in Section 3.

Figure 3: Example which illustrates the RLOS between multiple radars (4) and a single target. The radar positions are the red markers numbered (0-3). The x-axis, y-axis, and z-axis of the target UAV coordinate frame are the green, magenta, and yellow arrows respectively the target UAV position and coordinate frame is randomly simulated using translation, yaw, pitch, and roll homogeneous matrices.

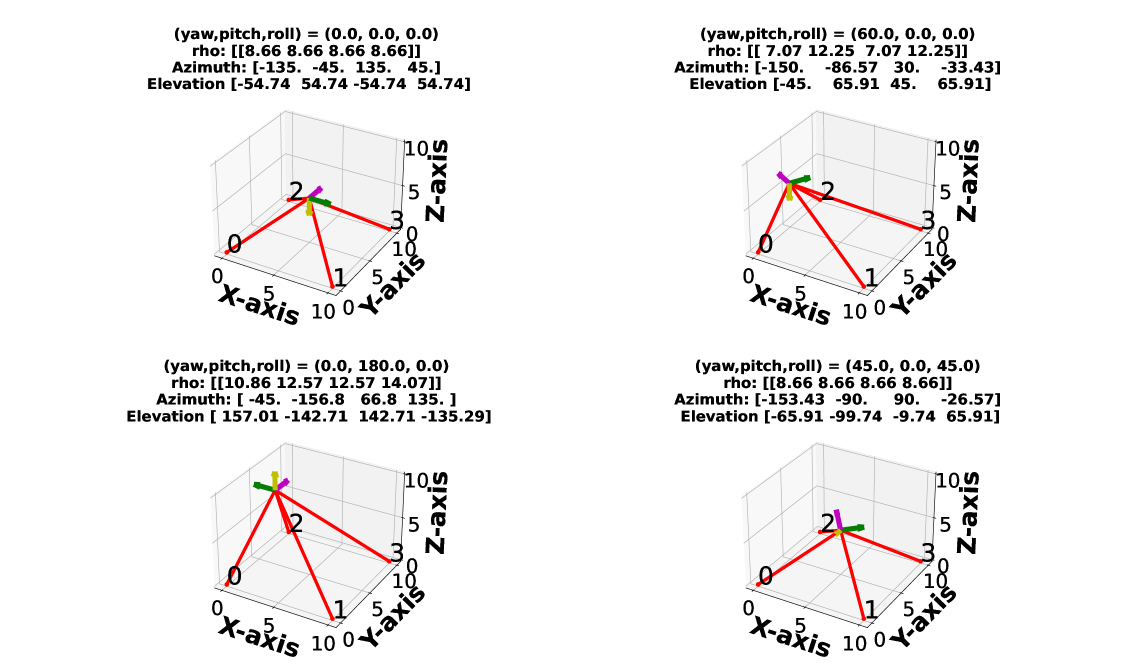
3.3 Testing Data Generation

We generate time series data of azimuth, elevation, and the corresponding RCS signature by simulating multiple RLOS to a target UAV being tracked for $L=100$ time steps along random walk trajectories. For each UAV type $c\in {𝒞}_{test}$, we generate $N_{test}$ trajectories such that $|{𝒟}_{test}|=|{𝒞}_{test}|N_{test}$. The target UAV trajectory follows a kinematic model of a drone moving at constant velocity $v_x=50[m/s]$ with random yaw and roll rotation jitters at a time resolution of $\mathrm{\Delta }t=0.1$ seconds:

	$d^{(t)}$	$=R_{{\gamma }^{(t-1)}}{R}_{{\alpha }^{(t-1)}}{R}_{{\beta }^{(t-1)}}{e}_x$			(2)
	${𝒰}^{(t)}$	$={𝒰}_d^{(t-1)}+v_x\mathrm{\Delta }t{d}^{(t)}$			(3)
	${\gamma }^{(t)}$	$={\gamma }^{(t-1)}+{ϵ}_{\gamma };$	${ϵ}_{\beta }\sim 𝒩(0^{\circ },{144}^{\circ })$		(4)
	${\alpha }^{(t)}$	$=0$			(5)
	${\beta }^{(t)}$	$={\beta }^{(t-1)}+{ϵ}_{\beta };$	${ϵ}_{\beta }\sim 𝒩(0^{\circ },{81}^{\circ })$		(6)

where the positive $x$-axis of the target UAV coordinate frame is the UAV ”forward facing” direction, $e_x$ is the x-axis unit vector, and $𝒰$ is the UAV position. The initial position and yaw of the target UAV is sampled uniformly at random:

	${\gamma }^{(0)}$	$\sim U(0,2\pi )$		(7)
	${𝒰}_d^{(t-1)}$	$\sim {[U(-150,150),U(-150,150),U(200,300)]}^T$		(8)

where the initial pitch and roll is 0.

Subsequently, at every time step $t$, the radars’ coordinate frames are transformed from the world coordinate frame to target coordinate frame:

	$\left[\begin{array}{c}\mathrm{\Delta }{x}^{(t)}\\ \mathrm{\Delta }{y}^{(t)}\\ \mathrm{\Delta }{z}^{(t)}\end{array}\right]=R_{{\alpha }^{(t)}}^{-1}{R}_{{\beta }^{(t)}}^{-1}{R}_{{\gamma }^{(t)}}^{-1}{(T^{(t)})}^{-1}𝒫$		(12)
	$𝒫=[p_1,p_2\mathrm{\dots }{p}_J]$		(13)

where $p_j$ is the world coordinates of radar $j$. The azimuth and elevation corresponding to each RLOS are found by converting from Cartesian coordinates to Spherical coordinates:

	${\rho }^{(t)}=\sqrt{{(\mathrm{\Delta }{x}^{(t)})}^2+{(\mathrm{\Delta }{y}^{(t)})}^2+{(\mathrm{\Delta }{z}^{(t)})}^2}$		(14)
	${\varphi }^{(t)}=\arctan \left({\displaystyle \frac{\mathrm{\Delta }{y}^{(t)}}{\mathrm{\Delta }{x}^{(t)}}}\right)$		(15)
	${\theta }^{(t)}=\delta (\mathrm{\Delta }{x}^{(t)}<0)\arccos \left({\displaystyle \frac{-\mathrm{\Delta }{z}^{(t)}}{{\rho }^{(t)}}}\right)$		(16)

where $\rho$ is the length of the RLOS to the target UAV. A single time step of a simulated UAV being tracked by multiple individual radars is depicted in Figure 3, featuring the displayed azimuths and elevations. The simulated azimuth and elevation time series data, ${\varphi }^{(1:t)}\in {ℛ}^{L\times J}\text{ and }{\theta }^{(1:t)}\in {ℛ}^{L\times J}$ respectively, is mapped to the measured RCS time series data $z^{(1:t)}\in {ℛ}^{L\times (JF)}$. Due to the symmetry of the drones, the measured RCS for any azimuth not between $[0,180]$ is approximated as the RCS corresponding to $\varphi =\varphi +180$. We note a negative $\mathrm{\Delta }z$ is used to align our target UAV coordinate frame with the experimental setup in [38], where the azimuth and elevation are calculated with respect to the bottom of the drone.

In summary, the test dataset ${𝒟}_{test}$ has the following structure:

${𝒟}_{test}={\{(z_i^{(1:L)},c_i)\}}_{i=1}^{N_{test}}$

(17)

where $z_i^{(t)}={[x_{i1}^{(t)},x_{i2}^{(t)},\mathrm{\dots },x_{iJ}^{(t)}]}^T$ and $i$ denotes the sample index and $j$ the radar index.

We train the discriminative ML model on the RCS, azimuth, and elevation measurements described in Section 3 Subsection 3.2, and evaluate our RATR framework on the trajectories described in Section 3 Subsection 3.3. We next discuss how these discriminative ML models are integrated into the RATR framework.

4 METHODOLOGY

At each time step $t$ multiple radars pulse EMWs at the target UAV, where each radar $j$ calculates a RCS signature, azimuth, and elevation $x_j$. Each radar inputs its respective observation to a local discriminative ML model to output a UAV type probability vector. Here, local denontes that the ML resides at the individual radar hardware. All the individual radar UAV type probability vectors are combined by a fusion method (Section 4 Subsection 4.2). Subsequently, the posterior UAV type probability distribution, based on the past RCS signatures $z^{(1:t-1)}$, is updated with the fused UAV type probability distribution from time step $t$. A RBC framework is applied such that the posterior probability distribution recursively updates as the radars continuously track a moving UAV. Our framework is shown in Figure 4.

Figure 4: RATR block diagram. Multiple radars continuously track and pulse an EMW at a moving UAV target. The each individual radar’s belief about the UAV type is at time step $t$ is fused in an Bayesian way and used to update recursively a posterior belief about the UAV type.

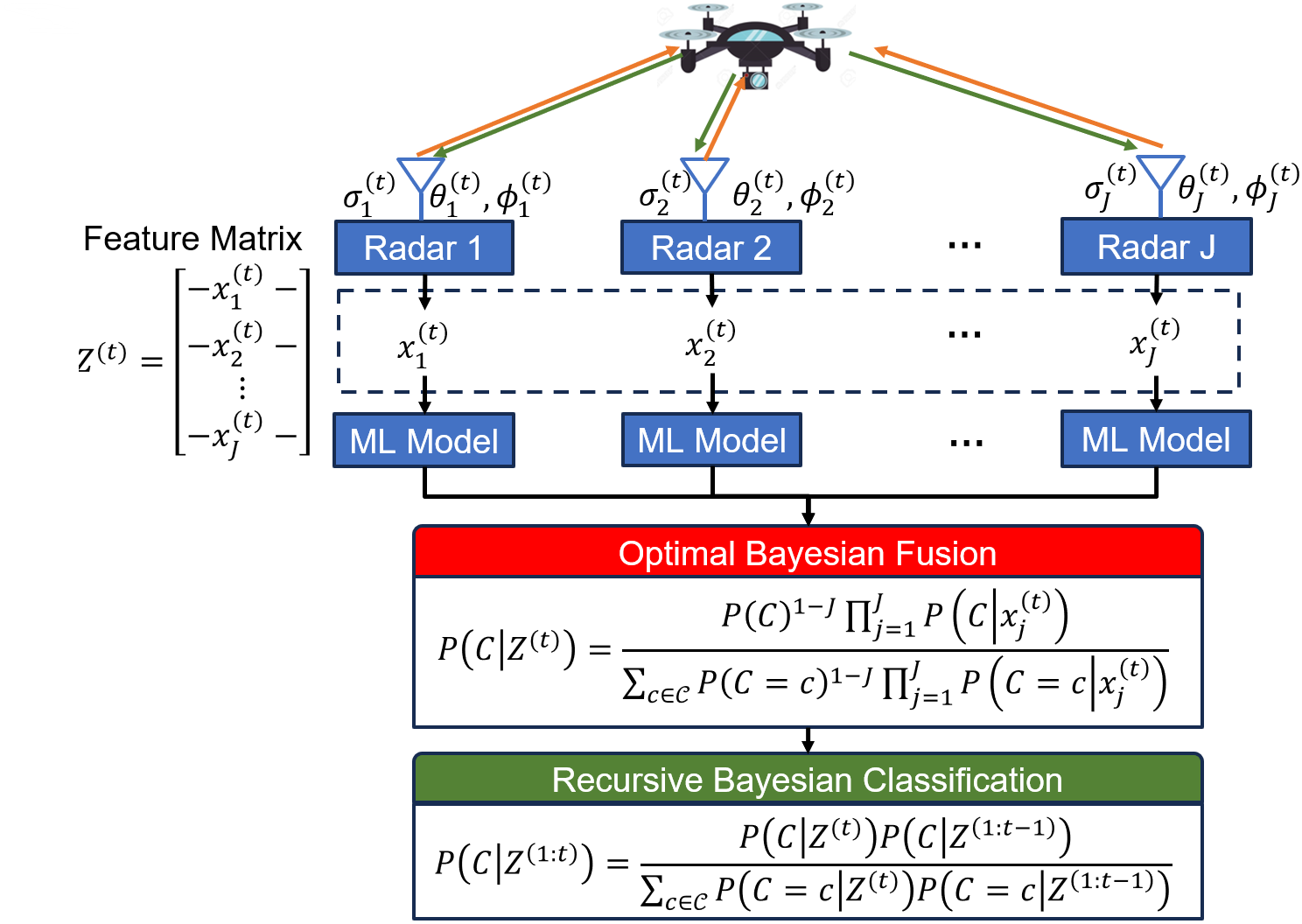
We focus on three discriminative ML models to generate individual radar UAV type probability vectors, which is described in the next subsection.

4.1 ML Models

In Logistic Regression, the model estimates the posterior probabilities of $|𝒞|$ classes parametrically through linear functions in $x$. It adheres to the axioms of probability, providing a robust framework for probabilistic classification [54]. The MLP, on the other hand, is a parametric model which estimates a highly nonlinear function. We use a FFNN architecture, where each neuron in the network involves an affine function of the preceding layer output, coupled with a nonlinear activation function (e.g., leaky-relu), with the exception of the last layer. For Logistic Regression and MLP, we use the Python Scikit-learn Python package LogisticRegression and MLPClassifier modules respectively; with the default hyperparameters (except the hidden layer size hyperparameter of [50,50,50]) [55]. XGBoost is a powerful non-parametric model that utilizes boosting with decision trees. In this ensemble method, each tree is fitted based on the residual errors of the previous trees, enhancing the model’s overall predictive capability [56]. We use the Python XGBoost package XGBClassifier module with the default hyperparameters [57].

4.2 Fusion Methods

The probability distribution $P(C|Z^{(t)})$ can leverage existing ML discriminative classification algorithms, including but not limited to as XGBoost, MLP, and Logistic Regression. For each ML model, we benchmark several radar RCS fusion methodologies: OBF, average, and maximum.

Figure 5: One data sample from the training test data is shown for illustrative purposes. The first subfigure (from the left) depicts four uniformly spaced radars tracking and classifying a target UAV navigating with a random walk trajectory. The second subfigure illustrates the evolution of the RBC posterior probability for the UAV type over time as more RCS, azimuth, and elevation measurements are collected. The third and fourth figures display the change in elevation from ground level and the top view of the X-Y position of the UAV over time, respectively.

4.2.1 Bayesian Optimal Fusion

The optimal fusion rule of the joint posterior distribution $p(C^{(t)}|Z^{(t)})$ is presented in [58, 37] as

$P(C|Z^{(t)})={\displaystyle \frac{P{(C)}^{(1-J)}{\prod }_{j=1}^{J}P(C|x_j^{(t)})}{{\sum }_{c=1}^{𝒞}P{(C=c)}^{(1-J)}{\prod }_{j=1}^{J}P(C=c|x_j^{(t)})}}$

(18)

The OBF method combines the individual radar probability vectors probabilistically, where the key assumption is conditional independence of the multiple individual radar observations at time step $t$ for a given UAV type: $P(x_1^{(t)},x_2^{(t)},\mathrm{\dots },x_J^{(t)}|C=c)={\prod }_{j=1}^{J}P(C|x_j^{(t)})$

4.2.2 Random

We use random classification probability vectors for the fusion method as a baseline of comparison. We denote the fused classification probability of $J$ individual radars as a sample from the Dirichlet Distribution $P(C|Z^{(t)})\sim Dir(\frac{1}{|𝒞|})$, which is equivalent to uniformly at random sampling from the simplex of discrete probability distributions.

4.2.3 Hard-Voting

Hard-voting involves selecting the UAV type that corresponds to the mode of decisions made by each individual radar discriminative ML model regarding UAV types [59].

$P(C=c|Z^{(t)})=\{\begin{array}{cc}1-\frac{|𝒞|ϵ}{|𝒞|+1}\hfill & \text{if }c=Mo(\widehat{c_1},\mathrm{\dots },\widehat{c_J})\hfill \\ \frac{ϵ}{|𝒞|}\hfill & \text{otherwise}\hfill \end{array}$

(19)

where $Mo$ denotes the mode function and $\widehat{c_j}$ denotes the maximum probability UAV type for radar $j$.

4.2.4 Soft-Voting

Soft-voting is the average of multiple individual ML model probability vectors. The UAV type with the highest average probability across all probability vectors is the final predicted UAV type. Averaging accounts for the confidence levels of each individual model, which provides a more nuanced method than hard-voting.

$P(C|Z^{(t)})={\displaystyle \frac{1}{J}}{\displaystyle \sum _{j=1}^J}P(C=c|x_j^{(t)})$

(20)

To benchmark our methodology, each individual radar operates within the same noisy channel (maintaining identical SNR) as they are closely geolocated. Consequently, the fusion method employed in this setup is analogous to the SNR fusion rule [28].

4.2.5 Maximum

We take the maximum ($\max$) class probability over multiple individual ML models. The max operator over random variables is known to be biased towards larger values, which will lead to worse classification performance [60].

$P(C|Z^{(t)})=\underset{j}{\max }P(C=c|x_j^{(t)})$

(21)

For each of the previously described fusion methods, when a new RCS measurement at time $t$ is observed, the fused UAV type probability distribution updates the recursively estimated UAV type posterior distribution.

4.3 Recursive Bayesian Classification

RBC with the OBF provides a principled framework for Bayesian classification on time-series data. As the radars’ dwell time on an individual target increases, the uncertainty and accuracy in the UAV type will decrease and increase respectively due to increased number of data observations. Furthermore, Bayesian methods are robust to situations with noisy data, which is common in radar applications (high clutter environments, multi-scatter points, and multi-path propagation). The RBC posterior probability for the UAV types is derived:

	$P(C|Z^{(1:t)})$	$={\displaystyle \frac{P(Z^{(t)}|C)P(C|Z^{(1:t-1)})}{{\sum }_{c=1}^{𝒞}P(Z^{(t)}|C=c)P(C=c|Z^{(1:t-1)})}}$
		$={\displaystyle \frac{\frac{P(C|Z^{(t)})\cancel{P(Z^{(t)})}}{\int P(C|Z^{\left(t\right)})P(Z^{\left(t\right)})}P(C|Z^{(1:t-1)})}{{\sum }_{c=1}^{𝒞}\frac{P(C=c|Z^{(t)})\cancel{P(Z^{(t)})}}{\int P(C=c|Z^{\left(t\right)})P(Z^{\left(t\right)})}P(C=c|Z^{(1:t-1)})}}$
		$={\displaystyle \frac{P(C|Z^{(t)})P(C|Z^{(1:t-1)})}{{\sum }_{c=1}^{𝒞}P(C=c|Z^{(t)})P(C=c|Z^{(1:t-1)})}}$		(22)

where we approximate the marginal distribution $P(C)=\int P(C|Z^{(t)})P(Z^{(t)})𝑑Z^{(t)}$ as a prior distribution, $\frac{1}{K}$, following previous papers [61, 62].

Next, we outline our approach to benchmarking the integration of the OBF method with the RBC within our RATR framework, establishing a fully Bayesian target recognition approach.

Figure 6: The RBC accuracy performance versus the number of radars increasing as a power of 2 (4, 16, 64 radars) for each discriminative ML model. The subfigures from left to the right increase the SNRdB and the term $J$ in the legend denotes the number of radars in a surveillance area.

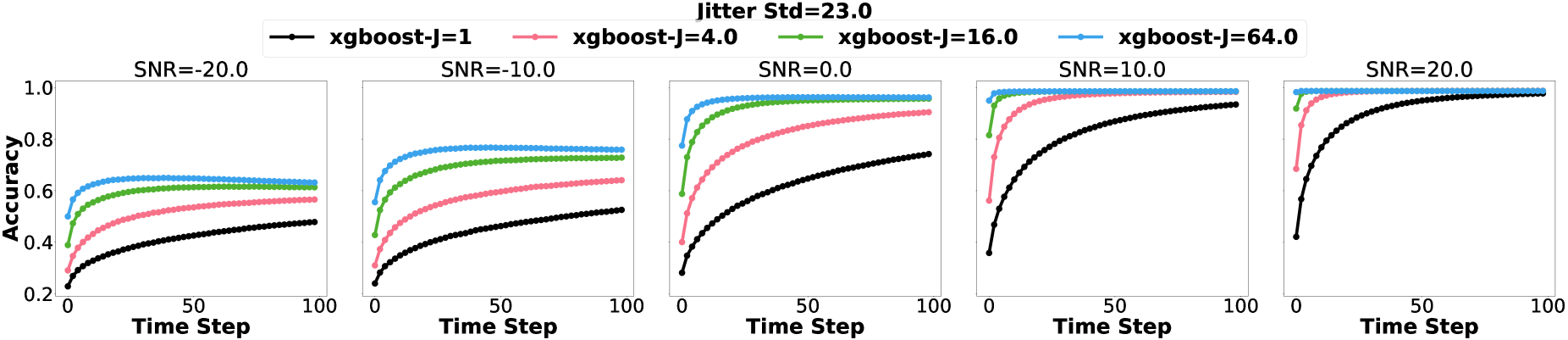
5 EXPERIMENTS

In the following subsections, we will describe the experimental setup and the assumptions made in our study to evaluate the performance of our proposed RATR for UAV type classification. We perform 10 Monte Carlo trials for each experiment and report the respective average accuracy. Through comprehensive analysis, we elucidate the impact of varying SNR levels and fusion methodologies on RATR.

5.1 Configuration

All experiments were run on Dual Intel Xeon E5-2650@2GHz processors with 16 cores and 128 GB RAM. The training dataset and the testing dataset sizes are 10000 samples and 2000 samples respectively. We make the follow assumptions in our simulations of multistatic radar for single UAV type classification:

1. multiple radar systems transmit and receive independent signals (non-interfering constructively or destructively) using time-division multiplexing,

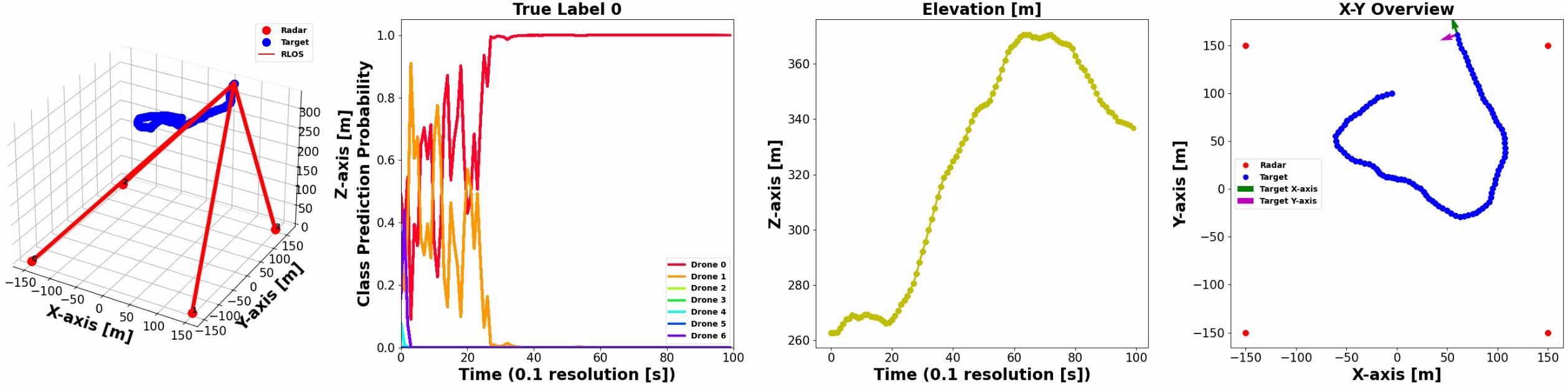
2. multiple radar systems continuously track a single UAV during a dwell time of 10 seconds (Figure 5 leftmost figure),

3. the azimuth and elevation of the incident EMW may be recovered with noise,

4. use of Additive Colored Gaussian Noise (ACGN) for the RCS signatures and uniform noise for the azimuth and elevations for noisy observations and

5. the $J$ radars are uniformly spaced in a 900m² grid on the ground level (Figure 5 leftmost figure).

We analyze radar configurations under various scenarios, including uniform radar spacing and a single radar placed at the (-150 [m], -150 [m]) corner of the grid. Randomly positioning radars within an boxed-area is excluded to prevent redundant stochastic elements, given the inherent randomness in the drone trajectories. Our investigation focuses on radar fusion method performance across various SNR settings and the number of radars in the multistatic configuration.

5.2 Signal-to-Noise Ratio

We apply ACGN to the measured RCS such as [34], but the units of the RCS signatures are dBm² units. The colored covariance matrix is generated as an outer product of a randomly sampled matrix of rank $F$:

	$M\sim 𝒩(0,I_F)$		(23)
	$\mathrm{\Sigma }=M{M}^T$		(24)

For each observed RCS signature ${\sigma }_i^{*}$ at time step $t$ and a specified SNR, we calculate the required noise power of the ACGN:

$Tr({\mathrm{\Sigma }}_i)={\displaystyle \frac{{\sum }_f{\sigma }_i^{*}{(f)}^2}{{10}^{\frac{SNR}{10}}}}$

(25)

where the trace of the covariance matrix is the total variance. We subsequently scale the covariance matrix to attain the desired SNR for sample $i$,

${\mathrm{\Sigma }}_i={\displaystyle \frac{{\mathrm{\Sigma }}_i}{Tr({\mathrm{\Sigma }}_i)}}{\displaystyle \frac{{\sum }_f{\sigma }_i^{*}{(f)}^2}{{10}^{\frac{SNR}{10}}}}$

(26)

and then add a sample realization of the ACGN to the observed RCS signature:

${\sigma }_i={\sigma }_i^{*}+ϵ$

$ϵ\sim 𝒩(0,{\mathrm{\Sigma }}_i)$

(27)

Additionally, to satisfy our third assumption of recovering the azimuth and elevation with noise, we add jitter uniformly at random to the ground truth azimuth and elevation with:

	$u_{\varphi },u_{\theta }$	$\sim U_{\varphi }(-a_{\varphi },a_{\varphi }),U_{\theta }(-a_{\theta },a_{\theta })$		(28)
	$\begin{array}{c}\hfill \varphi ={\varphi }^{*}+u_{\varphi }\end{array}\begin{array}{c}\hfill \theta ={\theta }^{*}+u_{\theta }\end{array}$			(29)

where $a_{\varphi }$ and $a_{\theta }$ determine the variance of uniform noise. We expect that our fully Bayesian RATR for UAV type will be more robust to low SNR environments.

5.3 Results

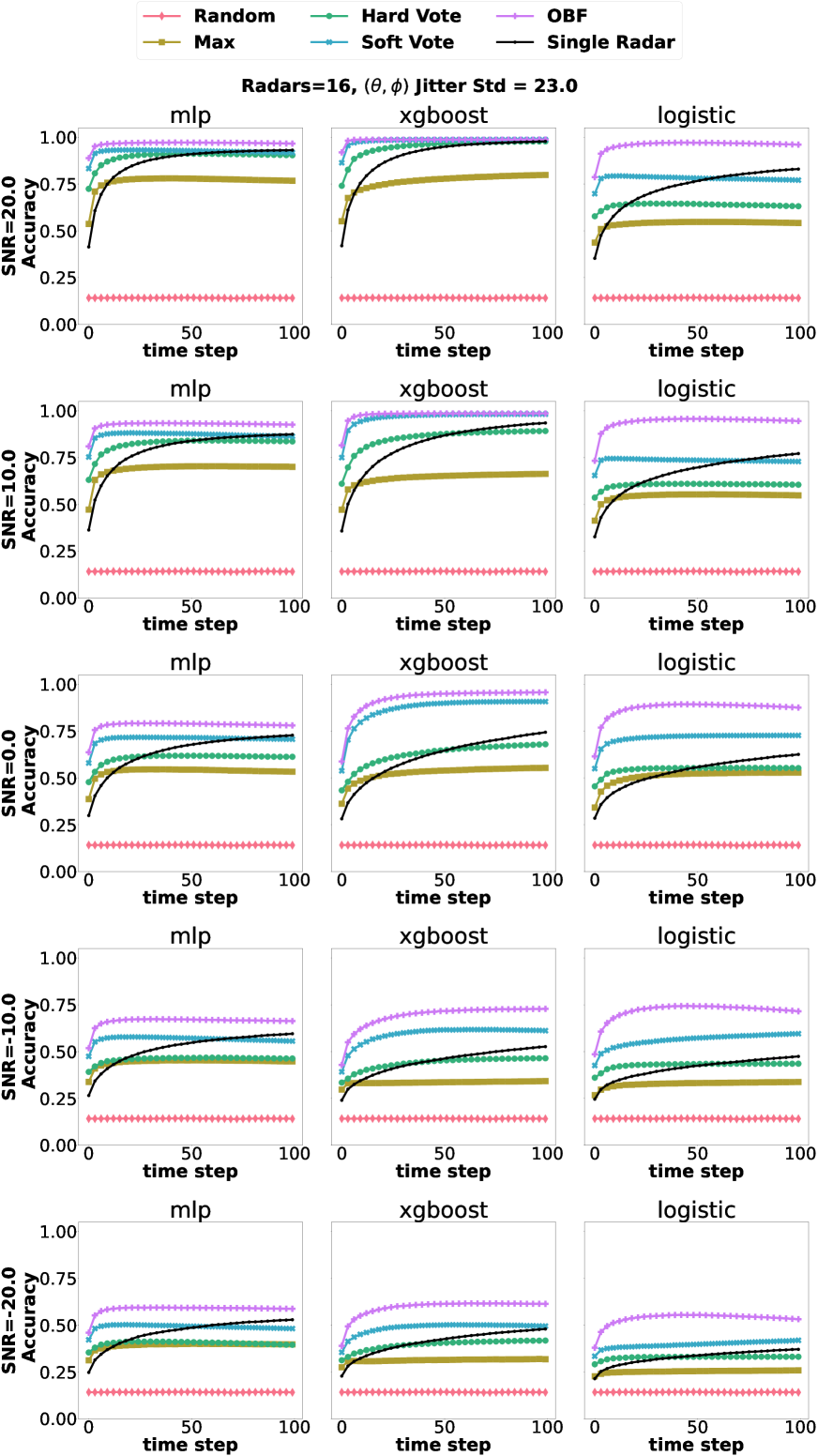
Using the optimal fusion method, namely the OBF method, results in substantial classification performance improvement in multistatic radar configurations compared to a single monostatic radar configurations (Figure 8,Figure 7).

Figure 7: Each figure axis specifies the SNR, with the first row displaying results with azimuth and elevation having a jitter standard deviation of 23, and the second row displaying results without azimuth and elevation. The bar color represents different fusion methods, and the line atop the bar indicates the 95% confidence interval over 10 Monte Carlo trials. All results are for 16 radars in a multistatic configuration, except single radar.

Figure 8: Each figure axis, where each row specifies the SNR and each column specifies the ML model, plots the RBC accuracy over time of 16 radars (and a single radar) for the OBF, soft-voting, hard-voting, single radar, and maximum fusion methods. The azimuth and elevation jitter standard deviations was $\approx$23.

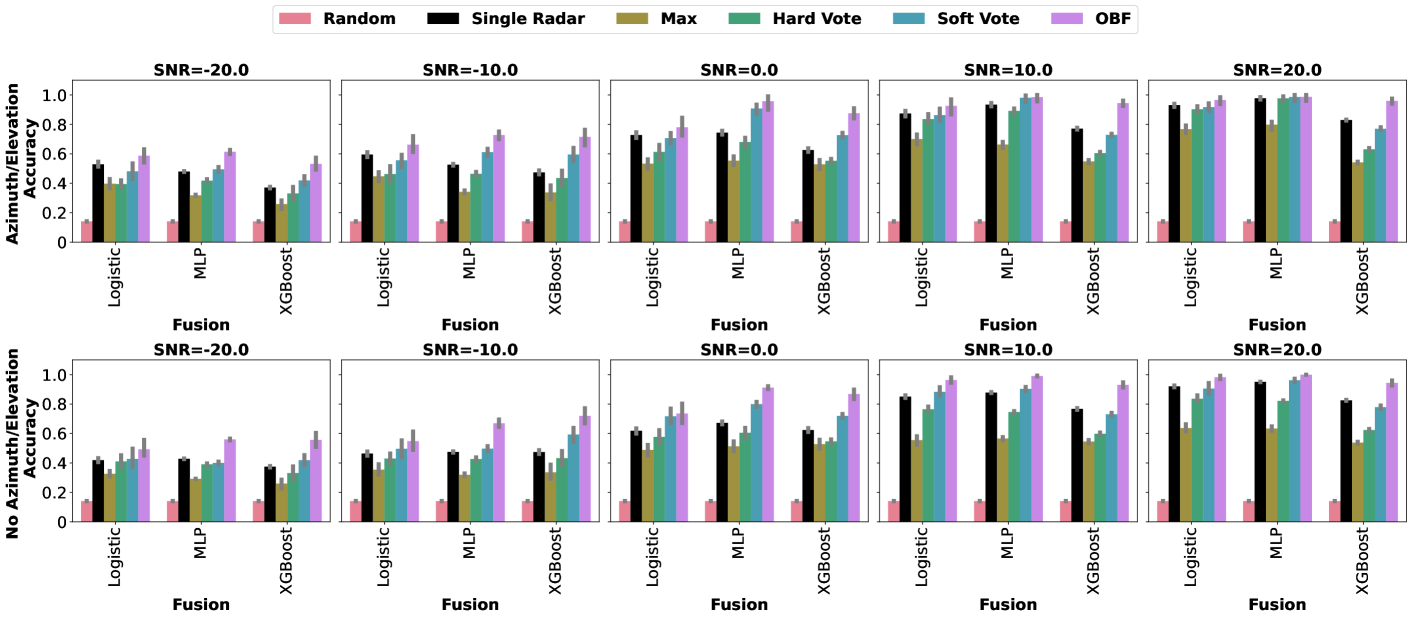
However, when using a fusion method not rooted in Bayesian analysis, such as the common SNR fusion rule, a single radar may outperform or exhibit similar classification performance in multistatic radar configurations provided there is a sufficient dwell time (Figure 8, the column of MLP and the column of Logistic Regressionand Figure 7). We also observed for the single radar and other fusion methods that various combinations of discriminative ML models and SNRs plateau at substantially lower classification accuracy compared to the OBF (Figure 8).

Increasing the number of radars within a surveillance area increases the different geometric views of the UAV, therefore providing a diverse UAV RCS signature at a specific time step $t$. We see that as the number of radars increases, the classification performance also increases under various SNR environments (Figure 6). Furthermore, increasing the number of radars in a surveillance area allows correctly classifying the target UAV type in a shorter period of time (on average).

We visualize the RBC accuracy as the SNR changes (Figure 7). We observe an ”S” curve by following the top of the barplot across columnns of figure axes, where an increase in the signal power does not lead to an increase in classification performance at the upper extremes of SNR. However, radar channels typically operate in the 0 to -20 dB SNR range. When the RATR is operating at lower SNR ranges, having more observations of the target UAV substantially improves the classification performance versus a single radar (Figure 6). If the SNR is high, the classification performance of a single radar should approach that of multi-radar classification, given a sufficiently large dwell time and suitable target geometries, especially when using a complex ML model (Figure 8).

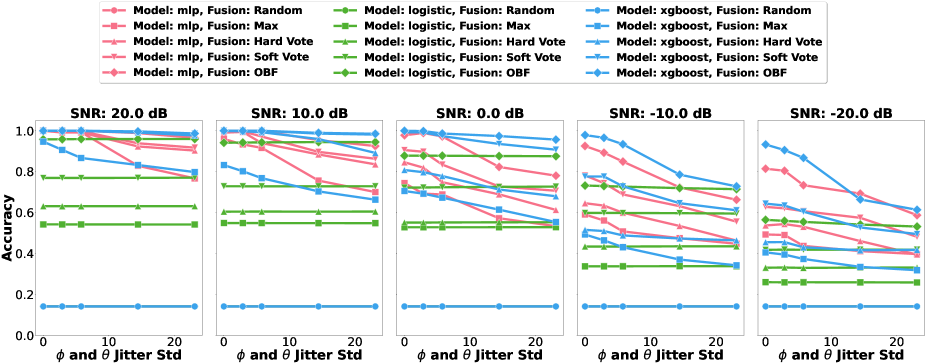
We assumed that azimuth and elevation of the incident EMW directed at the target UAV could be recovered for each radar, albeit with some noise. In the case of Logistic Regression, azimuth and elevation information does not seem to impact the classification decision. Increasing the standard deviation of the uniform noise jitter does not impact the classification accuracy. However, nonlinear discriminative ML models, such as MLP and XGBoost, leverage the interactions between the RCS signatures and the received azimuths and elevations, resulting in improved classification performance. Thus, for MLP and XGBoost, we observe that an increase in the standard deviation of uniform noise for azimuth and elevation leads to a decrease on the classification performance for lower SNR environments (Figure 9).

Figure 9: Each subfigure is the RBC accuracy for 16 radars versus the azimuth and elevation standard deviation of the uniform distribution. The subfigures from left to the right decrease the SNRdB. Each line color denotes a different discriminative ML model, and the line marker denotes the fusion method.

As an ablation study, we completely remove the azimuth and elevation information from the discriminative ML model training and inference. We observe that multistatic radar configurations still significantly improve RBC classification performance, and the OBF method remains the most effective fusion method (Figure 7).

6 CONCLUSION

This paper is the first to introduce a fully Bayesian RATR for UAV type classification in multistatic radar configurations using RCS signatures. We evaluated the classification accuracy and robustness of our method across diverse SNR settings using RCS, azimuth, and elevation time series data generated by random walk drone trajectories. Our empirical results demonstrate that integrating the OBF method with RBC in multistatic radar signifcantly enhances ATR. Additionally, our method exhibits greater robustness in lower SNR, with larger relative improvements observed compared to single monostatic radar and other non-trivial fusion methods. Thus, fully Bayesian RATR in multistatic radar configurations using RCS signatures improves both classification accuracy and robustness.

Future work will integrate radar-based domain-expert knowledge with Bayesian analysis, such that our method may incorporate radar parameters such as the range resolution or estimated SNR.

References

[1] W. Jiang, Y. Wang, Y. Li, Y. Lin, and W. Shen, “Radar target characterization and deep learning in radar automatic target recognition: A review,” Remote Sensing, vol. 15, no. 15, p. 3742, 2023.
[2] J. Eaves and E. Reedy, Principles of modern radar.   Springer Science & Business Media, 2012.
[3] X. Cai, M. Giallorenzo, and K. Sarabandi, “Machine learning-based target classification for mmw radar in autonomous driving,” IEEE Transactions on Intelligent Vehicles, vol. 6, no. 4, pp. 678–689, 2021.
[4] A. K. Maini, Military Radars, 2018, pp. 203–294.
[5] H. Learning. Unmanned aircraft systems / drones. [Online]. Available: https://rmas.fad.harvard.edu/unmanned-aircraft-systems-drones
[6] M. W. Lewis, “Drones and the boundaries of the battlefield,” Tex. Int’l LJ, vol. 47, p. 293, 2011.
[7] P. Mahadevan, “The military utility of drones,” CSS Analyses in Security Policy, vol. 78, 2010.
[8] D. Beesley, “Head in the clouds: documenting the rise of personal drone cultures,” Ph.D. dissertation, RMIT University, 2023.
[9] H. Shakhatreh, A. H. Sawalmeh, A. Al-Fuqaha, Z. Dou, E. Almaita, I. Khalil, N. S. Othman, A. Khreishah, and M. Guizani, “Unmanned aerial vehicles (uavs): A survey on civil applications and key research challenges,” IEEE Access, vol. 7, pp. 48 572–48 634, 2019.
[10] J.-P. Yaacoub, H. Noura, O. Salman, and A. Chehab, “Security analysis of drones systems: Attacks, limitations, and recommendations,” Internet of Things, vol. 11, p. 100218, 2020.
[11] E. Bassi, “From here to 2023: Civil drones operations and the setting of new legal rules for the european single sky,” Journal of Intelligent & Robotic Systems, vol. 100, pp. 493–503, 2020.
[12] T. Madiega, “Artificial intelligence act,” European Parliament: European Parliamentary Research Service, 2021.
[13] M. Elgan. Why consumer drones represent a special cybersecurity risk. [Online]. Available: https://securityintelligence.com/articles/why-consumer-drones-represent-a-special-cybersecurity-risk/
[14] J. Villasenor. Cyber-physical attacks and drone strikes: The next homeland security threat. [Online]. Available: https://www.brookings.edu/articles/cyber-physical-attacks-and-drone-strikes-the-next-homeland-security-threat/
[15] Y. Mekdad, A. Aris, L. Babun, A. El Fergougui, M. Conti, R. Lazzeretti, and A. S. Uluagac, “A survey on security and privacy issues of uavs,” Computer Networks, vol. 224, p. 109626, 2023.
[16] F. A. Administration. Uas sightings report. [Online]. Available: https://www.faa.gov/uas/resources/public_records/uas_sightings_report
[17] G. Markarian and A. Staniforth, Countermeasures for aerial drones.   Artech House, 2020.
[18] M. A. Richards, J. Scheer, W. Holm, and W. Melvin, “Principles of modern radar, raleigh, nc,” 2010.
[19] V. Chen and M. Martorella, “Inverse synthetic aperture radar,” SciTech Publishing, vol. 55, p. 56, 2014.
[20] M. Ezuma, C. K. Anjinappa, M. Funderburk, and I. Guvenc, “Radar cross section based statistical recognition of uavs at microwave frequencies,” IEEE Transactions on Aerospace and Electronic Systems, vol. 58, no. 1, pp. 27–46, 2022.
[21] C. Clemente, A. Balleri, K. Woodbridge, and J. J. Soraghan, “Developments in target micro-doppler signatures analysis: radar imaging, ultrasound and through-the-wall radar,” EURASIP Journal on Advances in Signal Processing, vol. 2013, no. 1, pp. 1–18, 2013.
[22] P. Klaer, A. Huang, P. Sévigny, S. Rajan, S. Pant, P. Patnaik, and B. Balaji, “An investigation of rotary drone herm line spectrum under manoeuvering conditions,” Sensors, vol. 20, no. 20, p. 5940, 2020.
[23] V. C. Chen, The micro-Doppler effect in radar.   Artech house, 2019.
[24] A. Manikas. Ee3-27: Principles of classical and modern radar: Radar cross section (rcs) & radar clutter. [Online]. Available: https://skynet.ee.ic.ac.uk/notes/Radar_4_RCS.pdf
[25] L. M. Ehrman and W. D. Blair, “Using target rcs when tracking multiple rayleigh targets,” IEEE Transactions on Aerospace and Electronic Systems, vol. 46, no. 2, pp. 701–716, 2010.
[26] P. Stinco, M. Greco, F. Gini, and M. La Manna, “Nctr in netted radar systems,” in 2011 4th IEEE International Workshop on Computational Advances in Multi-Sensor Adaptive Processing (CAMSAP), 2011, pp. 301–304.
[27] P. Stinco, M. Greco, F. Gini, and M. L. Manna, “Multistatic target recognition in real operational scenarios,” in 2012 IEEE Radar Conference, 2012, pp. 0354–0359.
[28] T. Derham, S. Doughty, C. Baker, and K. Woodbridge, “Ambiguity functions for spatially coherent and incoherent multistatic radar,” IEEE Transactions on Aerospace and Electronic Systems, vol. 46, no. 1, pp. 230–245, 2010.
[29] H. Meng, Y. Peng, W. Wang, P. Cheng, Y. Li, and W. Xiang, “Spatio-temporal-frequency graph attention convolutional network for aircraft recognition based on heterogeneous radar network,” IEEE Transactions on Aerospace and Electronic Systems, vol. 58, no. 6, pp. 5548–5559, 2022.
[30] D. J. Koehler, L. Brenner, and D. Griffin, “The calibration of expert judgment: Heuristics and biases beyond the laboratory,” Heuristics and biases: The psychology of intuitive judgment, pp. 686–715, 2002.
[31] E. C. Yu, A. M. Sprenger, R. P. Thomas, and M. R. Dougherty, “When decision heuristics and science collide,” Psychonomic bulletin & review, vol. 21, pp. 268–282, 2014.
[32] J. Q. Smith, Bayesian decision analysis: principles and practice.   Cambridge University Press, 2010.
[33] J. Baron, “Heuristics and biases,” The Oxford handbook of behavioral economics and the law, pp. 3–27, 2014.
[34] M. Ezuma, C. K. Anjinappa, V. Semkin, and I. Guvenc, “Comparative analysis of radar cross section based uav classification techniques,” arXiv preprint arXiv:2112.09774, 2021.
[35] A. Register, W. Blair, L. Ehrman, and P. K. Willett, “Using measured rcs in a serial, decentralized fusion approach to radar-target classification,” in 2008 IEEE Aerospace Conference, 2008, pp. 1–8.
[36] H. Cho, J. Chun, T. Lee, S. Lee, and D. Chae, “Spatiotemporal radar target identification using radar cross-section modeling and hidden markov models,” IEEE Transactions on Aerospace and Electronic Systems, vol. 52, no. 3, pp. 1284–1295, 2016.
[37] C. Bishop, “Pattern recognition and machine learning,” Springer google schola, vol. 2, pp. 531–537, 2006.
[38] V. Semkin, J. Haarla, T. Pairon, C. Slezak, S. Rangan, V. Viikari, and C. Oestges, “Drone rcs measurements (26-40 ghz),” 2019. [Online]. Available: https://dx.doi.org/10.21227/m8xk-dr55
[39] A. Rawat, A. Sharma, and A. Awasthi, “Machine learning based non-cooperative target recognition with dynamic rcs data,” in 2023 IEEE Wireless Antenna and Microwave Symposium (WAMS), 2023, pp. 1–5.
[40] V. Semkin, M. Yin, Y. Hu, M. Mezzavilla, and S. Rangan, “Drone detection and classification based on radar cross section signatures,” in 2020 International Symposium on Antennas and Propagation (ISAP), 2021, pp. 223–224.
[41] N. Mohajerin, J. Histon, R. Dizaji, and S. L. Waslander, “Feature extraction and radar track classification for detecting uavs in civillian airspace,” in 2014 IEEE Radar Conference, 2014, pp. 0674–0679.
[42] L. Lehmann and J. Dall, “Simulation-based approach to classification of airborne drones,” in 2020 IEEE Radar Conference (RadarConf20), 2020, pp. 1–6.
[43] I. Goodfellow, Y. Bengio, and A. Courville, Deep Learning.   MIT Press, 2016, http://www.deeplearningbook.org.
[44] L. Deng, “Artificial intelligence in the rising wave of deep learning: The historical path and future outlook [perspectives],” IEEE Signal Processing Magazine, vol. 35, no. 1, pp. 180–177, 2018.
[45] E. Wengrowski, M. Purri, K. Dana, and A. Huston, “Deep cnns as a method to classify rotating objects based on monostatic RCS,” IET Radar, Sonar & Navigation, vol. 13, no. 7, pp. 1092–1100, 2019.
[46] C. M. Bishop and H. Bishop, “The deep learning revolution,” in Deep Learning: Foundations and Concepts.   Springer, 2023, pp. 1–22.
[47] J. Mansukhani, D. Penchalaiah, and A. Bhattacharyya, “Rcs based target classification using deep learning methods,” in 2021 2nd International Conference on Range Technology (ICORT).   IEEE, 2021, pp. 1–5.
[48] B. Sehgal, H. S. Shekhawat, and S. K. Jana, “Automatic target recognition using recurrent neural networks,” in 2019 International Conference on Range Technology (ICORT).   IEEE, 2019, pp. 1–5.
[49] R. Fu, M. A. Al-Absi, K.-H. Kim, Y.-S. Lee, A. A. Al-Absi, and H.-J. Lee, “Deep learning-based drone classification using radar cross section signatures at mmwave frequencies,” IEEE Access, vol. 9, pp. 161 431–161 444, 2021.
[50] S. Zhu, Y. Peng, and G. C. Alexandropoulos, “Rcs-based flight target recognition using deep networks with convolutional and bidirectional gru layer,” in Proceedings of the 2020 the 4th International Conference on Innovation in Artificial Intelligence, 2020, pp. 137–141.
[51] M. A. Bansal, D. R. Sharma, and D. M. Kathuria, “A systematic review on data scarcity problem in deep learning: solution and applications,” ACM Computing Surveys (CSUR), vol. 54, no. 10s, pp. 1–29, 2022.
[52] A. Immer, M. Korzepa, and M. Bauer, “Improving predictions of bayesian neural nets via local linearization,” in International conference on artificial intelligence and statistics.   PMLR, 2021, pp. 703–711.
[53] D. Castelvecchi, “Can we open the black box of ai?” Nature News, vol. 538, no. 7623, p. 20, 2016.
[54] T. Hastie, R. Tibshirani, J. H. Friedman, and J. H. Friedman, The elements of statistical learning: data mining, inference, and prediction.   Springer, 2009, vol. 2.
[55] F. Pedregosa, G. Varoquaux, A. Gramfort, V. Michel, B. Thirion, O. Grisel, M. Blondel, P. Prettenhofer, R. Weiss, V. Dubourg, J. Vanderplas, A. Passos, D. Cournapeau, M. Brucher, M. Perrot, and E. Duchesnay, “Scikit-learn: Machine learning in Python,” Journal of Machine Learning Research, vol. 12, pp. 2825–2830, 2011.
[56] T. Chen and C. Guestrin, “Xgboost: A scalable tree boosting system,” in Proceedings of the 22nd acm sigkdd international conference on knowledge discovery and data mining, 2016, pp. 785–794.
[57]
[58] F. Pastor, J. García-González, J. M. Gandarias, D. Medina, P. Closas, A. J. García-Cerezo, and J. M. Gómez-de Gabriel, “Bayesian and neural inference on lstm-based object recognition from tactile and kinesthetic information,” IEEE Robotics and Automation Letters, vol. 6, no. 1, pp. 231–238, 2021.
[59] O. O. Awe, G. O. Opateye, C. A. G. Johnson, O. T. Tayo, and R. Dias, “Weighted hard and soft voting ensemble machine learning classifiers: Application to anaemia diagnosis,” in Sustainable Statistical and Data Science Methods and Practices: Reports from LISA 2020 Global Network, Ghana, 2022.   Springer, 2024, pp. 351–374.
[60] H. Van Hasselt, A. Guez, and D. Silver, “Deep reinforcement learning with double q-learning,” in Proceedings of the AAAI conference on artificial intelligence, vol. 30, no. 1, 2016.
[61] H. Calatrava, B. Duvvuri, H. Li, R. Borsoi, E. Beighley, D. Erdogmus, P. Closas, and T. Imbiriba, “Recursive classification of satellite imaging time-series: An application to water and land cover mapping,” arXiv preprint arXiv:2301.01796, 2023.
[62] N. Smedemark-Margulies, B. Celik, T. Imbiriba, A. Kocanaogullari, and D. Erdoğmuş, “Recursive estimation of user intent from noninvasive electroencephalography using discriminative models,” in ICASSP 2023 - 2023 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), 2023, pp. 1–5.

{IEEEbiography}

[]Michael Potter is a Ph.D. student at Northeastern University under the advisement of Deniz Erdoğmuş of the Cognitive Systems Laboratory (CSL). He received his B.S, M.S., and M.S. degrees in Electrical and Computer Engineering from Northeastern University and University of California Los Angeles (UCLA) in 2020, 2020, and 2022 respectively. His research interests are in recommendation systems, Bayesian Neural Networks, uncertainty quantification, and dynamics based manifold learning.

{IEEEbiography}

[]Murat Akcakaya (Senior Member, IEEE) received his Ph.D. degree in Electrical Engineering from the Washington University in St. Louis, MO, USA, in December 2010. He is currently an Associate Professor in the Electrical and Computer Engineering Department of the University of Pittsburgh. His research interests are in the areas of statistical signal processing and machine learning.

{IEEEbiography}

[] Marius Necsoiu (Member, IEEE) received his PhD in Environmental Science (Remote Sensing) from the University of North Texas (UNT), in 2000. He has broad experience and expertise in remote sensing systems, radar data modeling, and analysis to characterize electromagnetic environment behavior and geophysical deformation. As part of the DEVCOM ARL he leads research in cognitive radars and explores new paradigms in AI/ML science that are applicable in radar/EW research.

{IEEEbiography}

[] Gunar Schirner (S’04–M’08) holds PhD (2008) and MS (2005) degrees in electrical and computer engineering from the University of California, Irvine. He is currently an Associate Professor in Electrical and Computer Engineering at Northeastern University. His research interests include the modelling and design automation principles for domain platforms, real-time cyber-physical systems and the algorithm/architecture co-design of high-performance efficient edge compute systems.

{IEEEbiography}

[] Deniz Erdoğmuş (Sr Member, IEEE), received BS in EE and Mathematics (1997), and MS in EE (1999) from the Middle East Technical University, PhD in ECE (2002) from the University of Florida, where he was a postdoc until 2004. He was with CSEE and BME Departments at OHSU (2004-2008). Since 2008, he has been with the ECE Department at Northeastern University. His research focuses on statistical signal processing and machine learning with applications data analysis, human-cyber-physical systems, sensor fusion and intent inference for autonomy. He has served as associate editor and technical committee member for multiple IEEE societies.

{IEEEbiography}

[]Tales Imbiriba (Member, IEEE) is an Assistant Research Professor at the ECE dept., and Senior Research Scientist at the Institute for Experiential AI, both at Northeastern University (NU), Boston, MA, USA. He received his Doctorate degree from the Department of Electrical Engineering (DEE) of the Federal University of Santa Catarina (UFSC), Florianópolis, Brazil, in 2016. He served as a Postdoctoral Researcher at the DEE–UFSC (2017–2019) and at the ECE dept. of the NU (2019–2021). His research interests include audio and image processing, pattern recognition, Bayesian inference, online learning, and physics-guided machine learning.