Summary
The paper proposes a three-dimensional collision-free trajectory planning approach for unmanned aerial vehicles (UAVs) in low-altitude urban airspace using Automatic Dependent Surveillance-Broadcast (ADS-B) information. The key points are:
- 1. The low-altitude urban airspace is divided into multiple sub-airspaces to improve flight safety in UAV trajectory planning.
- 2. A secure sub-airspaces planning (SSP) algorithm based on dynamic programming, sliding window, and attraction mechanism is proposed for coarse-grained trajectory planning among sub-airspaces. This reduces the maximum number of UAVs in each sub-airspace.
- 3. A particle swarm optimization rapidly-exploring random trees (PSO-RRT) algorithm is designed for fine-grained trajectory planning within each sub-airspace. This considers both efficiency and cost to ensure safety and reduce energy consumption.
- 4. UAVs are equipped with ADS-B devices to enhance information acquisition and environmental perception capabilities. ADS-B information is leveraged for trajectory planning and re-planning.
- 5. Simulations verify that SSP reduces the maximum number of UAVs in sub-airspaces and total trajectory length, while PSO-RRT reduces trajectory cost compared to just using RRT or Bi-RRT algorithms.
In summary, the proposed approach leverages ADS-B, airspace division, the SSP algorithm, and the PSO-RRT algorithm to enable safe and efficient 3D collision-free UAV trajectory planning in complex low-altitude urban environments.
PSO-RRT algorithm
The particle swarm optimization-rapidly exploring random trees (PSO-RRT) algorithm is designed for trajectory planning within each sub-airspace. It combines the advantages of PSO and Bi-RRT to quickly locate optimal waypoints for UAVs while keeping a safe distance from obstacles. The main steps of the PSO-RRT algorithm are:
- 1. Multiple RRT and Bi-RRT trajectories are planned within the sub-airspace, serving as input data for PSO. An additional straight-line trajectory connecting the start and end points is added to prevent missing the optimal obstacle-free path.
- 2. The input trajectories are optimized using PSO by updating the individual best positions and global best positions of waypoints in each iteration. The iteration continues until convergence or the maximum number of iterations is reached.
- 3. PSO adjusts the positions of waypoints to find the minimum-cost UAV trajectory within the sub-airspace, considering both safety (distance from obstacles) and efficiency (trajectory length).
- 4. If a sudden obstacle appears during flight, the trajectory is re-planned using Bi-RRT between the two waypoints closest to the obstacle to avoid collision.
The cost function for evaluating trajectories considers the distance between waypoints and obstacles (both static and sudden) and the total trajectory length. Constraints are applied to limit the maximum distance between waypoints, total trajectory length, turning angle, pitch angle, and ensure waypoints stay within the sub-airspace boundaries.
PSO-RRT leverages the randomness of RRT for diversity, the greedy mechanism of Bi-RRT for shorter trajectories, and the optimization capabilities of PSO to find the best collision-free trajectory efficiently.
Assumptions
The paper does not provide detailed information about the specific characteristics of the ADS-B system or the UAVs used in the study. However, some assumptions and parameter settings can be inferred from the information provided:
ADS-B system:
- 1. The paper assumes that UAVs are equipped with ADS-B IN and ADS-B OUT devices, allowing them to broadcast and receive ADS-B messages.
- 2. ADS-B is expected to periodically and automatically broadcast the current positioning information of UAVs, enabling them to leverage the position information of other UAVs within the airspace.
- 3. Ground surveillance agencies are assumed to broadcast sudden obstacle information to the airspace via ADS-B.
- 4. The specific accuracy, latency, and update rate of the ADS-B system are not mentioned in the paper.
UAV characteristics:
- 1. The UAVs are assumed to have an onboard positioning system to determine their current position coordinates.
- 2. In the simulation experiments, the speed of UAVs is set to 5 m/s (Table III).
- 3. The maximum distance between adjacent trajectory points (l_max) is set to 40 m (Table I).
- 4. The maximum trajectory length within a sub-airspace (L_max) is set to 400 m (Table I).
- 5. The minimum and maximum turning angles between adjacent trajectory points (TA_min and TA_max) are set to -60° and 60°, respectively (Table I).
- 6. The minimum and maximum pitch angles between adjacent trajectory points (PA_min and PA_max) are set to -45° and 45°, respectively (Table I).
- 7. Specific acceleration limits of the UAVs are not provided in the paper.
It is important to note that these assumptions and parameter settings are based on the information provided in the paper. More detailed specifications of the ADS-B system and UAV characteristics might be needed for real-world implementation or further analysis of the proposed algorithms.
knowledge of the urban landscape
The paper makes several assumptions about the knowledge of the urban landscape for UAV trajectory planning:
- 1. The UAVs are assumed to possess positional information of all buildings (static obstacles) in the entire airspace A. This information includes the coordinates of the closest point of the building to the airspace origin and its dimensions in the x, y, and z axes.
- 2. The urban landscape is modeled using cuboids to represent buildings and other static obstacles. Each obstacle is represented by its closest position to the airspace origin and its length in the x, y, and z axes. For example, ((2, 2, 0), 2, 3, 4) indicates that the obstacle's closest position to the airspace origin is (2, 2, 0), with a length of 2 meters in the x-axis, 3 meters in the y-axis, and 4 meters in the z-axis.
- 3. The airspace A is divided into multiple sub-airspaces, which are assumed to be interconnected, independent, and equally sized grid cells. The number of sub-airspaces in each direction (x, y, and z) is predetermined.
- 4. The locations and dimensions of sudden obstacles, such as birds or non-cooperative UAVs, are not known a priori. However, when a sudden obstacle is detected by the ground surveillance center, its information is broadcast to the UAVs via ADS-B, allowing them to replan their trajectories accordingly.
- 5. In the simulation experiments, the obstacles are randomly generated within the airspace, with the height of the obstacles ranging from 25 to 240 meters (Table III).
These assumptions simplify the representation of the urban landscape and enable the proposed trajectory planning algorithms to operate effectively. However, in real-world scenarios, more detailed and accurate information about the urban landscape, such as 3D city models, might be required for optimal trajectory planning and obstacle avoidance.
Sensor Requirements and Capabilities
The paper does not explicitly mention the use of sensor data on the UAVs for trajectory planning or obstacle avoidance. The main focus is on leveraging ADS-B information for communication and information sharing among UAVs and ground stations.
Regarding the tracking and reporting of birds and non-cooperative UAVs, the paper assumes that ground surveillance agencies detect these sudden obstacles and broadcast their information to the airspace via ADS-B. However, the paper does not provide details on the specific sensors or the number of sensors required to track and report all birds and non-cooperative UAVs in the urban environment.
In a real-world scenario, detecting and tracking birds and non-cooperative UAVs would likely require a combination of various sensors, such as:
- Radar systems: Traditional radar or specialized avian radar systems can be used to detect and track birds and UAVs.
- Optical sensors: High-resolution cameras or infrared sensors can help detect and track birds and UAVs visually.
- Acoustic sensors: Microphone arrays can be used to detect and localize birds and UAVs based on their sound signatures.
- Cooperative tracking: ADS-B, as mentioned in the paper, can be used for tracking cooperative UAVs that broadcast their position information.
The number of sensors required would depend on factors such as the size of the urban area, the density of obstacles, the expected number of birds and non-cooperative UAVs, and the desired coverage and accuracy of the detection system. In a dense urban environment, a network of multiple sensors would likely be necessary to ensure comprehensive coverage and reliable detection of sudden obstacles.
It is important to note that the paper makes a simplifying assumption that ground surveillance agencies can detect and broadcast information about all birds and non-cooperative UAVs. In practice, developing a reliable and comprehensive detection system for these sudden obstacles would be a significant challenge requiring further research and development.
Feasability
Feasibility of the proposed concept has to be questionable, particularly regarding the ground sensor coverage and the challenges posed by the urban environment.
- 1. Ground sensor coverage: Even in airports where bird strikes are a significant concern, comprehensive detection and tracking of birds using ground sensors is a challenging task. Airports typically employ a combination of radar systems, visual observations, and other methods to mitigate bird strike risks, but complete coverage and real-time tracking of all birds remain difficult. In an urban environment, the problem becomes even more complex due to the larger area, more diverse obstacles, and the presence of non-cooperative UAVs.
- 2. Limited line of sight: Urban environments are characterized by tall buildings, structures, and other obstacles that can obstruct the line of sight for ground sensors. This limitation makes it difficult to achieve comprehensive coverage and reliable detection of birds and non-cooperative UAVs. Sensors would need to be strategically placed to minimize blind spots, but ensuring complete coverage would be a significant challenge.
- 3. ADS-B communication: The presence of tall buildings and other structures in urban environments can also affect the reliability of ADS-B communication. ADS-B signals can be blocked or reflected by obstacles, leading to degraded performance or loss of information. This issue can impact the ability of UAVs to receive timely information about sudden obstacles and the overall effectiveness of the proposed trajectory planning system.
- 4. Complexity and cost: Deploying and maintaining a large-scale network of ground sensors capable of detecting and tracking birds and non-cooperative UAVs in an urban environment would be a complex and costly endeavor. The system would require significant infrastructure, advanced sensors, data processing capabilities, and continuous maintenance to ensure its effectiveness.
Given these challenges, the assumption in the paper that ground surveillance agencies can comprehensively detect and report all birds and non-cooperative UAVs in an urban environment seems overly simplistic. In practice, a more realistic approach would likely involve a combination of onboard sensors on UAVs, limited ground sensor deployments in critical areas, and collaborative sensing among UAVs. Further research is needed to develop feasible and cost-effective solutions for detecting and avoiding sudden obstacles in urban UAV operations.
The limitations of ADS-B and GPS navigation in urban environments are well known in practice, which further highlight the challenges in implementing the proposed concept.
- 1. GPS position accuracy: As you mentioned, accurate 3D GPS positioning requires a clear line of sight to multiple satellites and a good geometric dilution of precision (GDOP). In urban environments, tall buildings and structures can obstruct satellite signals, leading to degraded GPS performance or even complete loss of position information varying with time of day. This issue can significantly impact the accuracy and reliability of ADS-B data, which relies on GPS for position reporting.
- 2. ADS-B data limitations: ADS-B data is indeed periodic and subject to transmission delays. The update rate of ADS-B messages is typically around 1-2 seconds, which may not be sufficient for real-time tracking and avoidance of sudden intruders, especially in dynamic urban environments. Moreover, the latency introduced by the transmission and processing of ADS-B data can further compound the problem, making it difficult to rely solely on ADS-B for time-critical obstacle avoidance.
- 3. Airport experience: My experience with the FAA for sensor fusion attempting to use ADS-B for tracking all vehicles on an airport to control runway incursions highlights the practical limitations of this technology. Airports, while more open than urban environments, still present challenges for GPS and ADS-B performance due to buildings, hangars, and other infrastructure. If ADS-B proved problematic in an airport setting, it would likely face even greater difficulties in a cluttered urban environment.
- 4. Sudden intruder detection: Relying on ADS-B for detecting and avoiding sudden intruders, such as birds or non-cooperative UAVs, becomes highly problematic given the limitations discussed above. The delayed and periodic nature of ADS-B data, combined with potential GPS inaccuracies in urban settings, would make it challenging to respond effectively to sudden threats.
These limitations suggest that the proposed concept of using ADS-B and ground sensors for comprehensive obstacle detection and avoidance in urban UAV operations may not be feasible in its current form. A more realistic approach would likely involve a multi-layered solution that combines:
- 1. Onboard sensors: UAVs equipped with cameras, lidars, or other sensors for real-time obstacle detection and avoidance.
- 2. Collaborative sensing: UAVs sharing sensor data and observations with each other to enhance situational awareness.
- 3. Improved navigation: Augmenting or replacing GPS with other navigation technologies, such as visual odometry or sensor fusion, to maintain accurate positioning in urban environments.
- 4. Predictive modeling: Developing advanced algorithms to predict the movement of sudden intruders based on available data and react accordingly.
Further research and development are needed to address the challenges posed by urban environments and create a robust, reliable, and practical system for UAV obstacle avoidance in these complex settings. The limitations highlighted in the paper and through your insights emphasize the need for a more comprehensive and realistic approach to this problem.
Three-Dimension Collision-Free Trajectory Planning of UAVs Based on ADS-B Information in Low-Altitude Urban Airspace
Electrical Engineering and Systems Science > Systems and Control
The environment of low-altitude urban airspace is complex and variable due to numerous obstacles, non-cooperative aircrafts, and birds. Unmanned aerial vehicles (UAVs) leveraging environmental information to achieve three-dimension collision-free trajectory planning is the prerequisite to ensure airspace security. However, the timely information of surrounding situation is difficult to acquire by UAVs, which further brings security risks.
As a mature technology leveraged in traditional civil aviation, the automatic dependent surveillance-broadcast (ADS-B) realizes continuous surveillance of the information of aircrafts. Consequently, we leverage ADS-B for surveillance and information broadcasting, and divide the aerial airspace into multiple sub-airspaces to improve flight safety in UAV trajectory planning. In detail, we propose the secure sub-airspaces planning (SSP) algorithm and particle swarm optimization rapidly-exploring random trees (PSO-RRT) algorithm for the UAV trajectory planning in law-altitude airspace.
The performance of the proposed algorithm is verified by simulations and the results show that SSP reduces both the maximum number of UAVs in the sub-airspace and the length of the trajectory, and PSO-RRT reduces the cost of UAV trajectory in the sub-airspace.
Submission history
From: Yiyang Liao [view email]
[v1]
Mon, 29 Apr 2024 05:22:47 UTC (1,869 KB)
Three-Dimension Collision-Free Trajectory Planning of UAVs Based on ADS-B Information in Low-Altitude Urban Airspace
Chao Dong, Yifan Zhang, Ziye Jia, Yiyang Liao, Lei Zhang, and Qihui Wu
This work was supported in part by the National Key R&D Program of China 2022YFB3104502, in part by National Natural Science Foundation of China under Grant 62301251, in part by the Natural Science Foundation of Jiangsu Province of China under Project BK20220883, in part by the open research fund of National Mobile Communications Research Laboratory, Southeast University (No. 2024D04), and in part by the Young Elite Scientists Sponsorship Program by CAST 2023QNRC001.
Chao Dong, Yifan Zhang, Yiyang Liao, Lei Zhang and Qihui Wu are with the College of Electronic and Information Engineering, Nanjing University of Aeronautics and Astronautics, Nanjing 211106, China (e-mail: dch@nuaa.edu.cn; yi- fanzhang123@nuaa.edu.cn; liaoyiyang@nuaa.edu.cn; Zhang_lei@nuaa.edu.cn; wuqihui@nuaa.edu.cn;).
Ziye Jia is with the College of Electronic and Information Engineering, Nanjing University of Aeronautics and Astronautics, Nanjing 211106, China, and also with the National Mobile Communications Research Laboratory, Southeast University, Nanjing 211111, China (e-mail: jiaziye@nuaa.edu.cn).
Corresponding author: Ziye Jia.
Index Terms—Three dimension trajectory planning of UAV, collision avoidance, sliding window, ADS-B, low-altitude urban airspace.
I. INTRODUCTION
ITH the advantages of high mobility and low cost, unmanned aerial vehicles (UAVs) are capable of many tasks such as air surveillance [1]–[3], freight delivering [4], auxiliary communication [5], [6] and computation [7], and disaster rescue [8]. Compared with other ground vehicles, the trajectories of UAVs are more flexible [9]. Besides, UAVs are able to select efficient trajectories to complete required tasks. UAVs are extensively utilized in low-altitude urban airspace owing to their cost-effectiveness, adaptability, and maneuverability. However, due to the limitation of endurance of UAVs, it is necessary to plan a collision-free trajectory within the energy constraints [10]. Furthermore, the incorrect acquisition of position information of UAVs may cause col- lisions with obstacles, which is unacceptable for low-altitude urban airspaces. The low-altitude urban airspace is character- ized by a complex and variable environment [11], featuring unforeseen events such as birds and non-cooperative UAVs. Due to limited environment perception of UAVs, the ground- assisted-airspace safety assessment becomes imperative, which requires swift information exchange among UAVs and ground surveillance agencies. Considering the above factors, the UAV must strategically plan a safe and viable trajectory within the energy constraints to fulfill the assigned task based on real-time airspace situational information during task execution.
A well-designed airspace division enhances the efficiency of UAV management systems. Drawing inspirations from the airspace corridors utilized by conventional civil aviation aircraft [12], [13], the airspace of UAV can also be divided into multiple designated tubes. By adhering to the pre-planned tubes, UAVs significantly reduce the probability of collision with obstacles. However, tubes lack flexibility and struggle to accommodate a large number of UAVs. An alternative approach to airspace division is stratification, which vertically segregates the airspace into distinct layers. This approach allows the airspace to accommodate more UAVs [14], but may compromise safety and operational efficiency [15]. Dividing the airspace into discrete grids is another commonly used method [16]. The grid approach allows for sequential traversal from initial to destination airspace, making it suitable for UAVs capable of vertical takeoff and landing. Compared with the tube method, the grid method leads to a higher collision probability, but this method effectively increases the number of UAVs that can be accommodated in the airspace. Additionally, it offers greater adaptability in UAV trajectory selection by refining airspace at the same altitude. In this paper, in order to make full use of the agility of UAVs, we divide the low-altitude urban airspace into multiple sub-airspaces.
As a mature technology employed in civil aviation surveil- lance, the automatic dependent surveillance broadcast (ADS-B) has the advantages of fast message update, low cost and rich information, the UAV enhances its airspace perception [31], enabling the acquisition of vital information and facilitating applications such as obstacle avoidance. In this paper, ADS- B device is equipped for UAVs to enhance the information acquisition and environmental perception capabilities.
A key prerequisite for UAVs to complete service tasks in low-altitude urban airspace is to plan a safe trajectory from the starting point to the endpoint without collisions [18]. Traditional trajectory planning methods include the artificial potential field (APF) [19], A∗ [20] and Dijkstra [21], and these methods are widely used in the trajectory planning of UAV in urban airspace. APF is commonly used for aircraft trajectory planning. In [22], the area around the destination is set as the gravitational field, and various types of obstacles are set as the repulsive field to incite collision during UAVs flight. Both Dijkstra and A∗ are efficient in searching the trajectory between the start and the destination [47]. Intelligent algorithm is another way to find the trajectory in the airspace, such as genetic algorithm (GA), ant colony optimization (ACO) [24] and particle swarm optimization (PSO) [25]. GA simulates the genetic mechanism and natural evolution of organisms in nature. ACO and PSO simulate the process of ant colony and bird flock to obtain food, respectively. These algorithms use the bionic mechanism of biological individuals or clusters to find trajectories and avoid collisions, which are simple to be implemented and have better optimization effect. As a sampling-based trajectory planning method, rapidly-exploring random trees (RRT), bidirectional rapidly-exploring random trees (Bi-RRT) and RRT∗ are often used in trajectory planning [26], [27]. These algorithms find a collision-free trajectory by randomly generating trajectory points and performing the shortest trajectory update and timely collision detection. However, much of the existing research focuses on the two-dimensional trajectory planning of UAVs, which makes it difficult to fully leverage the high maneuver- ability advantage of UAVs. This paper considers the variation of the UAV in the vertical direction during trajectory planning, making it more closely aligned with real-world scenarios.
In this work, RRT and Bi-RRT are leveraged as the basic
trajectory search algorithms, which are combined with the PSO algorithm
to optimize the trajectory. The main contributions of this paper are
summarized as follows:
- ) We divide the airspace into grids and utilize ADS- B as information source for UAVs to obtain airspace status information. Meanwhile, ground stations broadcast information about sudden obstacles to UAVs via ADS-B, allowing for trajectory readjustment.
- ) We propose a secure sub-airspaces planning (SSP) algo- rithm based on dynamic programming, sliding window, and attraction mechanism for trajectory planning among sub-airspaces for UAVs. The coarse-grained trajectory is dynamically adjusted based on the status of airspace, reducing the maximum number of UAVs in the sub- airspace.
- ) We design the particle swarm optimization-rapidly ran- dom trees (PSO-RRT) algorithm for trajectory planning within the sub-airspace, which considers both efficiency and cost to ensure safety and reduce energy consumption in UAV trajectories. The performance of PSO-RRT is sufficiently demonstrated via simulation results.
The organization of this paper is as follows: Section II in-
troduces the related research works. In Section III, the problem
expatiation and designed algorithms are presented. Section IV provides
the simulation results. Finally, the conclusion is drawn in Section V.
II. RELATED WORKS
There exist a couple of researches focusing on UAV trajectory planning conducted by researchers. In this work, we primarily focus on three interconnected research fields: the integration of UAVs and ADS-B systems, airspace design for UAVs and UAV trajectory planning.
ADS-B enhances the situational awareness ability of UAVs in low-altitude airspace and the surveillance ability of ground stations. [28] studies the cooperative perception and avoidance among UAVs equipped with ADS-B, proposes a planning algorithm based on RRT, and the simulation results show that in frontal encounter conflict, the UAV equipped with the RRT based algorithm successfully realizes the conflict resolution by leveraging ADS-B. In the context of UAV trajectory predic- tion, [29] proposes a centralized UAV trajectory surveillance architecture with ADS-B in low-altitude airspace, and predicts the ADS-B trajectory. The long short-term memory (LSTM) is leveraged to train the UAV ADS-B information, and the simulation results reveal that the proposed algorithm has higher prediction accuracy by leveraging ADS-B information. In [30], the safety of utilizing ADS-B in UAVs is investigated, and an algorithm for distinguishing fake UAV ADS-B information is proposed, ensuring the data security of UAVs. The utilization of ADS-B for trajectory monitoring and planning on UAVs shows potential, but there exist limited researches specifically focusing on utilizing UAV ADS-B data for trajectory planning. In the domain of civil aviation, the division of airspace holds the potential to augment both flight safety and airspace utilization for aircrafts. Hence, the airspace division can also enhance the efficiency and safety of UAVs. [33] proposes an airspace grid division model based on GPS signals and wind strength, which effectively enhances the utilization of airspace. [34] divides the urban airspace into multiple grids and adjusts their sizes based on the degree of danger, enabling risk avoidance in UAV trajectory planning. [35] subdivides the urban airspace into a series of grids and utilizes a designed cost function for UAV trajectory planning among grids. The results demonstrate that in various application scenarios, grids signif- icantly enhance the airspace utilization of UAVs. [36] models the urban infrastructure in the three-dimensional airspace and conducts comparative experiments on trajectory planning using three methods: grid, tube, and trajectory points. The results demonstrated that compared with the other algorithms, the grid method has the highest UAV capacity and throughput. In conclusion, the grid method strikes a balance between efficiency and safety in UAV trajectory planning.
In the scenario of cargo transportation by UAVs in urban airspace, [37] redesigns the cost estimation function of A∗ to enable the planned trajectory to consider both the efficiency and cost of goods delivery, thus achieving rapid trajectory planning. In [38], according to the changes in the airspace, trajectory planning is performed using the A∗ and RRT∗ algorithms, respectively. When the airspace situation is stable, the UAV utilizes the A∗ algorithm. However, when the airspace changes and the original trajectory becomes invalid, the trajectory is optimized by adjusting the selection probability and range of trajectory points in the RRT∗ algorithm to adapt to the changing airspace. Although traditional methods are easy to implement, the planned trajectories tend to be rigid, making it difficult to fully leverage the advantages of agile flight for UAVs.
RRT and its variants efficiently compute collision-free tra- jectories within specified airspace. In the context of unknown environmental information and unavailable GPS signals, [42] explores the application of RRT∗ for small UAVs in locat- ing the source of hazardous chemical leaks. By leveraging the utilization and exploration mechanism, RRT∗ generates candidate trajectories limited to the sensor’s sensing range which optimizes computational resources and enables real- time trajectory planning. [43] aims to swiftly determine shorter UAV flight trajectories within the airspace, this study utilizes the RRT algorithm based on a greedy approach for trajectory planning to minimize unnecessary bends. The algorithm reduces search complexity and requires only a few trajectory points. In densely populated low-altitude airspace with static and dynamic obstacles, [44] models static threats and predicts dynamic threats using the RRT algorithm. By employing this model, the RRT∗ algorithm is utilized for trajectory planning in complex airspace. The algorithm exhibits a high obstacle penetration rate. However, the RRT algorithm and variants are known for randomness, making it challenging to find the optimal trajectory within the airspace for UAVs.
As an important part of intelligent
algorithm, PSO has been applied in UAV trajectory planning. [39]
combines simulated annealing and PSO to realize autonomous trajectory
planning of UAVs. The random disturbance mechanism of simulated
annealing algorithm is used to assist PSO to jump out of local minimum
value and avoid falling into local optimum. The simulation results show
that the algorithm has higher trajectory quality. [40] leverages PSO
to generate the UAV trajectory in complex three-dimensional
environment. The results show that the PSO algorithm satisfies the
requirements of real-time trajectory planning for UAVs. Based on the
above analysis, PSO demonstrates excellent performance in solving
optimization problems related to UAV trajectories.
III. PROBLEM EXPATIATION AND ALGORITHM DESIGN
In
this section, the low-altitude urban airspace is divided into
multiple sub-airspaces, and the SSP algorithm is proposed to achieve
trajectory planning among sub-airspaces. The PSO-
RRT algorithm is also designed to achieve trajectory planning within each sub-airspace.
A. Airspace division
Airspace division is beneficial for UAVs in low-altitude urban airspace. It enables better warning and avoidance of conflicts with obstacles. Additionally, when planning UAV trajectories, only obstacles within the current sub-airspace need to be considered, which reduces complexity compared to considering all obstacles in the entire airspace. On the left side of Fig. 1, the airspace where the UAV Ui works is designated as a large area A, which contains buildings of different heights and ADS- B ground stations. UAV Ui only provides services to users within airspace A, which means Ui will not fly out of the boundaries of A. On the right side of Fig. 1, A is divided into interconnected, independent, and equally sized multi-layer grid sub-airspace SA = SA1 , SA2 , ..., SAn , ..., SAN . Ax is the number of sub-airspaces in the x direction, Ay is the number of sub-airspaces in the y direction, and Az is the number of sub- airspaces in the z direction. The number of the grids is in the order of x direction first and then y direction layer by layer. In Fig. 1, the number of sub-airspaces in all three directions is 5, which means the airspace A is divided into 125 sub-airspaces.
B. Trajectory planning
The UAV trajectory planning consists of two main parts. Firstly, the UAV utilizes SSP for trajectory planning among sub- airspaces to find continuous coarse-grained trajectory C S =
{C S1 , C S2 , ..., C Sm , ..., C SM }, a coarse-grained trajectory
consists of M continuous sub-airspaces. C S1 and C SM are re-
spectively indicate the starting sub-airspace and the destination
sub-airspace. Subsequently, a fine-grained trajectory planning is performed by PSO-RRT within each specific sub-airspace in C S. This paper assumes that the UAV possesses positional information of all buildings in A and can determine its current position coordinates Pi using an onboard positioning system, and the destination coordinates, Pe . UAVs in airspace A are
equipped with ADS-B IN and ADS-B OUT devices, allowing for broadcasting
and receiving ADS-B messages, respectively. Since ADS-B can
periodically and automatically broadcast the current positioning
information of UAVs, UAVs leverage the position
information broadcasted by other UAVs within the airspace and sudden
obstacle information broadcasted by ground surveillance agencies to
conduct trajectory planning be- tween sub-airspaces and trajectory
re-planning in sub-airspace.
1) Trajectory planning among sub-airspaces: The UAV Ui utilizes the SSP algorithm to search for C S and executes two steps. Firstly, Ui determines the starting sub-airspace C S1 and the destination sub-airspace C SM based on coordinating Pi and Pe . Then, leveraging dynamic programming, Ui plans a coarse-grained trajectory C S composed of sub-airspace between C S1 and C SM . In Fig. 1, the C S1 and C S11 of Ui are respectively SA102 and SA24 , and the continuous red sub-airspaces represent C S. C S can achieve a multitude of combination possibilities by utilizing different sub-airspaces. Therefore, it is necessary to establish evaluation criterias for comparisons.
In formula (1), C Tn denotes the cost of Ui in sub-airspace SAn , On denotes the number of static obstacles in SAn , and The sliding window of ܵܣଶ Plane between sub-airspaces
The sliding window of ܵܣଷଶ
AECn denotes the number of UAVs in SAn . k1 and k2 are polynomials, in particular, k1 + k2 = 1, k1, k2 > 0, and k1 ≫ k2:
C Tn = k1· On + k2· AECn . (1) The function expressed by formula (2) serves as a quantita-
tive measure for evaluating the performance of different C S
configurations:
N
C Tsn = C Ti . (2)
i=1
Subsequently, the sub-airspaces in C S are optimized in problem P 0 to minimize the associated cost:
P 0 : min C Tsn (3)
CS
To reduce the probability of collision, a sliding window is designed as a component in the SSP algorithm. In detail, the working process of the sliding window for trajectory planning among sub-airspaces is illustrated in Fig. 2. When Ui enters SA27 , formula (2) and dynamic programming algorithm are utilized to obtain the new C S. The sub-airspaces SA27 , SA32 , SA31 , and SA6 within the blue dashed area are selected as the sliding window when Ui enters SA32 . When Ui moves from SA27 to SA32 , maintaining SA32 , SA31 , and SA6 in the sliding window. formula (2) and dynamic programming algorithm are employed again to obtain the new C S. The sub- airspaces within the red solid box are selected as the sliding window when UAV Ui enters SA32 . This process of sliding the sub-airspace window is repeated when UAV Ui enters a new sub-airspace, until there are less than four sub-airspaces remained. The length for the sliding window needs to be carefully determined. When the length is too large, it will result in a delay in perceiving the overall spatial situation, which is not conducive to avoiding sub-airspaces with a large number of UAVs. Conversely, when the length is too small, in Fig. 2, the length of sliding window is 1. When UAV Ui enters SA32 ,
the endpoint will lie on the plane between SA32 and SA31 . the position could be P 1 or P 2. If the endpoint of Ui is P 1, it leads to a long path in SA31 ,
which means more energy consumption and higher probability of
conflicts. However, when the length of sliding window is 4, the endpoint
P 2 is determined by attraction mechanism. P 2 shortens the trajectory in SA31 ,
which results in energy savings and lower probability of conflicts.
Therefore, a window length of 4 is set for SSP to achieve a balance
among computational power, energy consumption, and safety.
The endpoint position of a sub-airspace will affect the trajectory length of Ui .
In order to shorten the trajectory length and save energy consumption,
the SSP leverages an attraction mechanism which attracts the endpoint
on the basis of sliding windows. The plane where the endpoint belongs is
divided into different regions according to the direction of the
sub-airspaces in sliding window. If two directions of the sub-airspace
in the sliding window change, as shown in Fig. 3, the plane is divided
into four areas. According to the change in the direction of the
sub-airspaces, the endpoint can be limited to one area which shorten the
length of trajectory in next sub-airspace. If only one direction of the
sub-airspace in the sliding window changes, the plane will be divided
into two parts, which still have certain performance improvement
compared with completely randomly finding the endpoint. If the direction
has no change, the selection of the endpoint is completely random,
and the attraction mechanism will lose effect.
2) Trajectory planning in sub-airspace: After finding coarse grained trajectory C S for UAV Ui , more precise trajectory planning needs to be performed within the sub-airspace. In order to make full use of the advantages of PSO and Bi-RRT, PSO-RRT algorithm is formulated for Ui to achieve quickly locating the trajectory points of UAVs while keeping them away from obstacles.
The distance between UAV Ui and obstacles needs to keep a safe range to ensure safe flight. Therefore, it is necessary to model the obstacles to calculate the distance between them. The obstacles can be divided into the static obstacle and sudden
obstacle. The red cuboid in Fig. 4 represents a static obstacle, which mainly includes ground buildings. The space of static obstacle can be divided into two layers. The top layer consists of 9
The trajectory planning of UAV Ui in sub-airspace SAn is shown in Fig. 5. The red cuboid OBOE, OBand O B represents static obstacle, while the yellow cuboid represents a sudden obstacle SO, which is already appeared before Ui
entering SAn. The green points Pn = pl_, P2, ..., P j , ... , P ]
are the planned trajectory points for ui within the sub-airspace
SAn. Trajectory P j point in Pn consists of three-dimensional
sub-spaces, while the bottom layer, excluding the obstacle itself,
coord.
n n
P x )' P y)'
d n
P z )·
mates j(
j( an j(
has 8 sub-spaces, resulting in a total of 17 subspaces. UAV
swarms, as typical multi-agent systems, rely on cooperation among individual agents for collision avoidance [49] and the implementation of optimal control [48] to effectively address UAV conflict avoidance. Another method to achieve collision free flights between UAVs is to define the flight range of the evading UAV as a sudden obstacle. Sudden obstacles appear within the same sub-airspace of UAVs, such as birds and non cooperative UAVs. In Fig. 4, different from the static obstacles, the sudden obstacles are divided into three layers, with each layer respectively containing 9, 8, and 9 subspaces, and in total 26 subspaces. The method for calculating the distance between the UAV and the sudden obstacle is the same as the static obstacle. The size and position of the sudden obstacle may change, and this model facilitates observation and dynamic adjustment of its range with flexibility.
In the trajectory planning process, obstacles are represented by their closest position to the airspace origin, with a length
The vectors between two adjacent trajectory points in the x , y, and z directions are shown in formula (4) to formula (6). The horizontal vector and the distance between two adjacent trajectory points are represented by formula (7) and formula (8), respectively. The turning angle T Aand the pitch angle P A
of Ui in S An are obtained through formula (9) and formula (10).
origin is (2, 2, 0), with a length of 2 meters in the x-axis, a
J ( j( j -
length of 3 meters in the y-axis, and a length of 4 meters in the z-axis. The difference between sudden obstacles and static
n n n
qj (z) Pj( z ) - Pj-l(z)·
(10)
obstacles is that the coordinates of a sudden obstacle can have a z-value greater than 0, and the rest of the representation is
ui evaluates the cost of the planned trajectory in the sub
airspace through formula (11):
In formula (11), On denotes the number of static obstacles in SAn , Mn denotes the number of sudden obstacles, lobj(e) indicates the distance between jth trajectory point of Ui and the eth static obstacle, and lsoj(e) denotes the distance between jth trajectory point of Ui and the eth sudden obstacle. J is the number of trajectory points of Ui in SAn . Lj+1 denotes the distance between adjacent trajectory points pn and pn+1 . k3, global optimum of all paths.
Updates the velocity, position, and optimization function values for each particle.
j j Update the historical
k4, k5, and k6 are coefficients, and if the number of static
obstacles or sudden obstacles is 0, the parameters k5 or k6 are set as 0, respectively.
The positions of the trajectory points in Pn are optimized in problem P 1 to find a trajectory with the minimum cost:
optimum of each path and the global optimum of all paths.
Whether the maximum No number of iterations
has been reached?
P 1 : min C SAi
(12)
Pn n
Yes
s.t. C 1 : Lj+1 < lmax ,
q−1
Get the optimal path
C 2 :
j=1
Lj+1 < Lmax ,
Fig. 6. The process of PSO-RRT.
faster calculation of collision-free trajectories with shorter tra- jectory lengths. However, Bi-RRT makes the trajectory closer PSO and Bi-RRT, we formulate PSO-RRT to achieve quickly locating
the waypoints of UAVs while keeping them away from obstacles. Fig. 6
illustrates the proposed PSO-RRT algorithm for sub-airspace trajectory
planning based on PSO, RRT, and In constraint C 1, lmax denotes the maximum length between adjacent trajectory points, and in constraint C 2, Lmax denotes the maximum length of the trajectory in SAn . In constraints C 3 and C 4, T Amax and P Amax denote the maximum turn- ing angle and pitch angle between adjacent trajectory points, respectively, while T Amin and P Amin denote the minimum turning angle and pitch angle between adjacent trajectory points. Constraints C 5, C 6, and C 7 denote the position range constraints that each trajectory point of the UAV needs to keep in safe ranges.
In
the process of trajectory planning, it is necessary to consider
both the distance between UAVs and obstacles and the length of the
trajectory. The length of the trajectory indicates the energy
consumption during UAV flight, while the distance between UAVs and
obstacles represents the flight safety. PSO is an optimization algorithm
inspired by the foraging behavior of birds. It has the fast convergence
speed and simple imple- mentation, which is effective in solving
optimization problems. RRT is leveraged to find trajectories with no
conflict within a specified range. It has fast computation speed and
generates random trajectories. Bi-RRT is a variant of the RRT algorithm
which adds a greedy mechanism in searching progress, enabling
Bi-RRT. Multiple RRT and Bi-RRT trajectories are planned within sub-airspace SAn ,
which serve as input data for PSO. An additional trajectory
connecting the starting point to the endpoint is added as another set
of input data to prevent the RRT algorithm from missing the optimal
obstacle-free trajectory. The input data is optimized employing the
PSO, updating the individual best positions and global best positions of
trajectory points in each UAV trajectory during each iteration. The
iteration process continues until the entire optimization function
converges or the maximum number of iterations is reached. PSO-RRT can
make full use of the randomness of RRT, providing greater diversity
in the input data. Bi-RRT provides trajectory data with shorter lengths
for the optimization process. PSO quickly optimizes the input data,
adjusts the position of trajectory points, and finds the UAV trajectory
with the minimum cost within SAn .
There
are two situations in PSO-RRT when dealing with sud- den obstacles.
Firstly, when PSO-RRT is conducting trajectory planning, a sudden
obstacle has already appeared. In such case, the treatment of sudden
obstacles is the same as static obstacles. Secondly, while the UAV is
flying within the sub-airspace, a sudden obstacle appears against the
planned trajectory. In this
TABLE I
ܱܵ
Fig. 7. Trajectory re-planning for sudden obstacles in SAn .
situation, it is necessary to re-plan the trajectory within the sub-airspace to avoid the conflict.
As shown in Fig. 7, when UAV Ui is flying within SAn according to the pre-planned trajectory points, the surveillance center detects the occurrence of a sudden obstacle SOq within SAn . The surveillance center transmits the information of to the ground station and broadcasts it to airspace via
ADS-B. Upon receiving this message, Ui in SAn calculates whether there is a conflict with the planned trajectory of SOq . If there is no conflict, Ui continues to fly according to the current trajectory. If there is a conflict with SOq , a trajectory re-planning is required. In Fig. 7, the red trajectory points represent the points that Ui cannot
reach due to conflicts, the yellow trajectory points are the two
original trajectory points closest to the sudden obstacle SOq , the green trajectory points are the original trajectory points planned before entering SAn , and the blue trajectory points are the new trajectory points generated by re-planning. Ui leverages the two yellow trajectory points as the starting and ending points for trajectory re-planning in SAn , and utilizes Bi-RRT to generate new blue trajectory points to avoid conflicts with SOq .
IV. SIMULATION RESULTS
A. Trajectory planning in sub-airspace
The parameter settings in SAn are shown in Table I, and the parameter settings of the PSO-RRT algorithm are shown in Table II.
The
simulation results of cost function are shown in Fig. 8, in detail,
there is at least one obstacle between the starting point and the
endpoint of each esimulation. Each simulation leverages three
algorithms to calculate their cost function values. The trajectories
planned by RRT and Bi-RRT are the input data for PSO-RRT. It can be seen
that the cost function value of the trajectory planned in each group of
PSO-RRT is smaller than the cost function value of the trajectory
planned by the RRT and Bi-RRT algorithms. The reason lies in that the
trajectory planned by the two algorithms is leveraged as the input data
and the PSO is leveraged to adjust the optimization result.
The top view and side view of the trajectory planned by
the three algorithms in SAn are respectively shown in Fig.
9a
and Fig. 9b. The green trajectory in Fig. 9a is the smoothed trajectory
planned by RRT. Since the algorithm planned by RRT has strong
randomness, it may lead to a longer trajectory length. The yellow
trajectory is planned by Bi-RRT. It is observed that due to its own
unique trajectory length greedy mechanism, the trajectory is shorter
than the other two algorithms. However, the shorter trajectory brings a
more radical planning strategy, which means the trajectory is close to
the obstacle, making Ui easy to
collide with the obstacle if there exists an error in positioning. The
blue trajectory is the trajectory planned by PSO-RRT for SAn .
Compared with the yellow and green trajectory, the blue one maintains a
shorter trajectory length and avoids two obstacles between the second
and sixth trajectory points, achieving a farther distance from the
obstacle, which means that PSO-RRT considers the factors of security.
Even if there is a deviation in positioning, it can still safely reach
the endpoint through static obstacles.
Fig. 10 shows the relationship
between cost function value and iterations in the planning process.
At the beginning of the iteration, the minimum cost function value of
all trajectories is 103.94. With the continuous increment of
iterations, PSO constantly adjusts all trajectories until the final
cost function value converges to 99.98, and the blue trajectory in Fig.
10 is obtained. Via the change process of fitness value, it is concluded
that the trajectory obtained by final optimization must have a lower
cost than the trajectory before optimization.
In Fig. 11, the UAV has planned the trajectory to be taken for
trajectory point. Therefore, the sudden obstacle is added to the static obstacle list. Taking the coordinates of the fourth trajectory point as the starting point and the coordinates of the sixth trajectory point as the endpoint, Bi-RRT is leveraged to quickly re-plan the trajectory, and the re-planned trajectory is smoothed to replace the original conflict trajectory. When the UAV is located at the fourth trajectory point, the new trajectory is executed to avoid the yellow sudden obstacle.
B. Trajectory planning among sub-airspaces
After the whole airspace is divided, the trajectory planning is carried out to verify the effect of sliding window and attraction mechanism. The parameter settings of the experiment are shown in Table III.
The obstacle distribution of the whole airspace A in the
the current sub-airspace, but the monitoring center observes that there exist sudden obstacles in the sub-airspace, and broadcasts the obstacle information to the airspace through the ADS-B ground station. After receiving the ADS-B information, the UAV in the sub-airspace detects that the fifth trajectory point is located in the sudden obstacle, resulting in the failure of the trajectory between the fourth trajectory point and the sixth
experimental setting is shown in Fig. 12. SSP and three trajec tory planning algorithms are employed with same environment settings. The sub-airspace in C S is: (SA1, SA2 , S A27 , SA32 , SA33, S A34, S A39, S A44, 89 ). The black trajectory point is
the trajectory planned by SSP and RRT, and the blue trajectory point is the trajectory planned by SSP and Bi-RRT. It is observed that the distance between the trajectory point and the obstacle is very close in the whole trajectory. The red point is the trajectory planned by SSP and PSO-RRT, and the trajectory point maintains a large distance from the obstacle.
TABLE III
(a) Top view of trajectory planning in airspace A.
In Fig. 13, we set the number of UAVs in airspace A as
50, and randomly generate 5 sets of starting points and endpoints
for these UAVs. The trajectory between the starting point and the
endpoint includes at least 5 sub-airspaces. Each set of simulations only
leverages SSP and no sliding window method for UAVs. The trajectory of
no sliding window is determined before take off. In the simulation,
the maximum number of UAVs in the sub-airspace of the two trajectory
planning methods during the entire UAV flight is recorded. It is
observed that the maximum number of UAVs in the sub-
Fig. 14. The number of UAVs in each sub-airspace in simulation index 5.
space domain of SSP is smaller than that of trajectory planning without sliding window, which further guarantees the safety.
Fig. 14 is the distribution of the maximum number of UAVs in SA1 to SA125 of
the fifth index of simulations in Fig. 13, leveraging SSP and
trajectory planning without sliding window. The maximum number of UAVs
in the sub-airspace of SSP is
3, while the maximum number of UAVs
in the sub-airspace without sliding window is 6, which are larger than
the results of SSP. The reason is that the sliding window adjusts
the subsequent sub-airspace trajectory according to the number of UAVs
in the whole sub-airspace broadcast by ADS-B ground station when the
UAV enters the new sub-airspace, which effectively reduces the maximum
number of UAVs in each sub- airspace. The trajectory of no sliding
window is fixed before the UAV takes off, so when the number of UAVs in
the airspace is very large. The subsequent trajectory cannot be
adjusted.
In Fig. 15, five sets of simulations are carried out and
the first four are randomly generated. There are at least five sub-
airspaces between the starting point and the endpoint. The fifth
simulation is set specially, and its starting point and the endpoint are respectively SA1 and SA5 with
no direction change. As shown in Fig. 15, in the first four groups of
simulations, due to the change of direction among the sub-airspace
trajectories, the attraction mechanism reduces the range of the
sub-airspace endpoint in the trajectory planning process and reduces the
total trajectory length. However, the trajectory planning without the
attraction mechanism has a longer trajectory length because the
endpoint in the sub-airspace is completely randomly selected.
In the fifth simulation, since there is no change in the direction of CS, the attraction mechanism fails, which is the same as the completely random search for the endpoint of the sub-airspace. Therefore, the length of the trajectory in the sub-airspace with the attraction mechanism is longer.
V. CONCLUSION AND FUTURE WORK
In this paper, in order to enhance the information acquisition and environmental perception capabilities, UAVs in low-altitude urban areas are equipped with ADS-B devices to achieve high-frequency information exchange. In order to enhance the safety and efficiency of UAVs, we divide the low-altitude urban airspace into multiple sub-airspaces, and leverage ADS B to continuously monitor flight for each sub-airspace. On the basis of airspace division, we propose SSP algorithm based on dynamic programming, sliding window and attraction mech anism to conduct coarse-grained trajectory planning among sub-airspaces, and we propose the PSO-RRT algorithm for trajectory planning in sub-airspaces. The results of multiple simulations prove that the maximum number of UAVs in sub airspaces and the total length of trajectory are both reduced by SSP. As for the trajectory planning in sub-airspace, the PSO RRT algorithms reduce the cost of trajectory compared with the trajectory planned by RRT and Bi-RRT, which means the trajectory planned by PSO-RRT simultaneously considers both safety and efficiency. In conclusion, the collision-free trajectory planning for UAVs within the airspace has been successfully implemented by SSP and PSO-RRT with ADS-B information.
To further investigate the real-time performance, UAV peak values in airspace, and average computation time of the pro posed algorithm, we just constructed a set of ADS-B OUT and ADS-B IN devices leveraging Raspberry Pi, position ing modules, and software-defined radio equipment to test the algorithm's performance. In addition, in future work, we will incorporate cooperation between UAVs into UAV conflict avoidance considerations, and consider the impact of NACv and NACp on ADS-B message reception, conducting more practical experiments for validation using the ADS-B devices we have constructed.
REFERENCES
[1] Y. Zhu, Z. Jia, Q. Wu, C. Dong, Z. Zhuang, H. Hu, and Q. Cai, "UAV trajectory tracking via RNN-enhanced IMM-KF with ADS-B data," arXiv preprint arXiv:2312.15721, 2023.
[2] A. V. Savkin and H. Huang, "Bioinspired bearing only motion camouflage UAV guidance for covert video surveillance of a moving target," IEEE Syst. J, vol. 15, no. 4, pp. 5379-5382, 2021.
[3] H. Huang, A. V. Savkin, and W. Ni, "Online UAV trajectory planning for covert video surveillance of mobile targets," IEEE Trans. Au tom. Sci. Eng, vol. 19, no. 2, pp. 735-746, 2022.
[4] W. Park, X. Wu, D. Lee, and S. J. Lee, "Design, modeling and control of a top-loading fully-actuated cargo transportation multirotor," IEEE Rob. Autom. Lett, vol. 8, no. 9, pp. 5807-5814, 2023.
[5] Z. Jia, M. Sheng, J. Li, D. Niyato, and Z. Han, "LEO-satellite-assisted UAV: Joint trajectory and data collection for Internet of remote things in 6G aerial access networks," IEEE Internet of Things Journal, vol. 8, no. 12, pp. 9814-9826, 2021.
[6] Z. Wang, J. Guo, Z. Chen, L. Yu, Y. Wang, and H. Rao, "Robust secure UAV relay-assisted cognitive communications with resource allocation and cooperative jamming," J. Commun. Networks, vol. 24, no. 2, pp.
139-153, 2022.
[7] Z. Jia, Q. Wu, C. Dong, C. Yuen, and Z. Han, "Hierarchical aerial computing for Internet of things via cooperation of HAPs and UAVs," IEEE Internet of Things Journal, vol. 10, no. 7, pp. 5676-5688, 2023.
[8] J. Xu, K. Ota, and M. Dong, "Big data on the fly: UAV-mounted mobile edge computing for disaster management," IEEE Trans. Network Sci. Eng, vol. 7, no. 4, pp. 2620-2630, 2020.
[9] W. Kaifang, L. Bo, G. Xiaoguang, H. Zijian, andY. Zhipeng, "A learning based flexible autonomous motion control method for UAV in dynamic unknown environments," J. Syst. Eng. Electron, vol. 32, no. 6, pp. 1490-
1508, 2021.
[10] H.-T. Ye, X. Kang, J. Joung, and Y.-C. Liang, "Optimization for wireless powered loT networks enabled by an energy-limited UAV under practical energy consumption model," IEEE Wireless Commun. Lett, vol. 10, no. 3, pp. 567-571, 2021.
[11] W. Yang, J. Tang, R. He, andY. Chen, "A medium-term conflict detection and resolution method for open low-altitude city airspace based on temporally and spatially integrated strategies," IEEE Trans. Control Syst. Techno!, vol. 28, no. 5, pp. 1817-1830, 2020.
[12] M. Shanmugavel, A. Tsourdos, R. Zbikowski, and B. White, "3D path planning for multiple UAVs using pythagorean hodograph curves," in AIAA Guidance, navigation and control conference and exhibit, Hilton Head, South Carolina, USA, 2007.
[13] R. Ehrmanntraut and S. McMillan, "Airspace design process for dynamic sectorisation," in 2007 IEEEIAIAA 26th Digital Avionics Systems Confer ence, Dallas, TX, USA, 2007.
[14] J. M. Hoekstra, J. Maas, M. Tra, and E. Sunil, "How do layered airspace design parameters aifect airspace capacity and safety?" in 7th international conference on research in air transportation, Philadelphia, Pennsylvania, USA, 2016.
[15] L. Sedov and V. Polishchuk, "Centralized and distributed UTM in layered airspace," in 8th International Conference on Research in Air Transportation, Castelldefels, Catalonia, Spain, 2018.
[16] B. Pang, W. Dai, T. Ra, and K. H. Low, "A concept of airspace configuration and operational rules for UAS in current airspace," in
2020 AIAAIIEEE 39th Digital Avionics Systems Conference (DASC), San
Antonio, TX, USA, 2020.
[17] C. Wei and Y. Dai, "A design of communication interface of ADS-B for UAV," in 2014 Seventh International Symposium on Computational Intelligence and Design, vol. 1, Hangzhou, China, 2014.
[18] J. Lee and V. Friderikos, "Interference-aware path planning optimization for multiple UAVs in beyond 5G networks," J. Commun. Networks, vol. 24, no. 2, pp. 125-138, 2022.
[19] X. Yuan, Y. Hu, D. Li, and A. Schmeink, "Novel optimal trajectory design in UAV-assisted networks: A mechanical equivalence-based strategy," IEEE J. Sel. Areas Commun, vol. 39, no. 11, pp. 3524-3541, 2021.
[20] Y. Cai, Q. Xi, X. Xing, H. Gui, and Q. Liu, "Path planning for UAV
tracking target based on improved A-star algorithm," in 2019 1st Inter
national Conference on Industrial Artificial Intelligence (!AI), Shenyang, China, 2019.
[21] M. T. S. Ibrahim, S. V. Ragavan, and S. Ponnambalam, "Way point based deliberative path planner for navigation," in 2009 IEEEIASME In-
11
ternational Conference on Advanced Intelligent Mechatronics, Singapore,
2009.
[22] M. Qian, Z. Wu, and B. Jiang, “Cerebellar model articulation neural network-based distributed fault tolerant tracking control with obstacle avoidance for fixed-wing UAVs,” IEEE Trans. Aerosp. Electron. Syst,
2023.
[23] Y. Pan, Y. Yang, and W. Li, “A deep learning trained by genetic algorithm to improve the efficiency of path planning for data collection with multi- UAV,” Ieee Access, vol. 9, pp. 7994–8005, 2021.
[24] J. Li, Y. Xiong, and J. She, “UAV path planning for target coverage task in dynamic environment,” IEEE Internet Things J, 2023.
[25] Y. Liu, H. Pan, G. Sun, A. Wang, J. Li, and S. Liang, “Joint scheduling and trajectory optimization of charging UAV in wireless rechargeable sensor networks,” IEEE Internet Things J, vol. 9, no. 14, pp. 11 796–11 813,
2021.
[26] L. Tan, Y. Zhang, J. Huo, and S. Song, “UAV path planning simulating drive’s visual behavior with RRT algorithm,” in 2019 Chinese Automation Congress (CAC), Hangzhou, China, 2019, pp. 219–223.
[27] C. Jiang, Z. Hu, Z. P. Mourelatos, D. Gorsich, P. Jayakumar, Y. Fu, and M. Majcher, “R2-RRT*: Reliability-based robust mission planning of off- road autonomous ground vehicle under uncertain terrain environment,” IEEE Trans. Autom. Sci. Eng, vol. 19, no. 2, pp. 1030–1046, 2021.
[28] C. Zhao, J. Gu, J. Hu, Y. Lyu, and D. Wang, “Research on cooperative sense and avoid approaches based on ADS-B for unmanned aerial vehi- cle,” in 2016 IEEE Chinese Guidance, Navigation and Control Conference (CGNCC), Nanjing, China, 2016.
[29] Y. Zhang, Z. Jia, C. Dong, Y. Liu, L. Zhang, and Q. Wu, “Recurrent LSTM-based UAV trajectory prediction with ADS-B information,” in GLOBECOM 2022 - 2022 IEEE Global Communications Conference, Rio de Janeiro, Brazil, 2022.
[30] Z. P. Languell and Q. Gu, “Securing ADS-B with multi-point distance- bounding for UAV collision avoidance,” in 2019 IEEE 16th International Conference on Mobile Ad Hoc and Sensor Systems (MASS), Monterey, CA, USA, 2019.
[31] Y. Liao, L. Zhang, Z. Jia, C. Dong, Y. Zhang, Q. Wu, H. Hu, and B. Wang, “Impact of UAVs equipped with ADS-B on the civil aviation monitoring system,” in 2023 IEEE/CIC International Conference on Communications in China (ICCC), Dalian, China, 2023.
[32] Z. Shen, X. Cheng, S. Zhou, X.-M. Tang, and H. Wang, “A dynamic airspace planning framework with ADS-B tracks for manned and un- manned aircraft at low-altitude sharing airspace,” in 2017 IEEE/AIAA
36th Digital Avionics Systems Conference (DASC), St. Petersburg, FL, USA, 2017.
[33] Q. Shao, R. Li, M. Dong, and C. Song, “An adaptive airspace model for quadcopters in urban air mobility,” IEEE Trans. Intell. Transp. Syst, vol. 24, no. 2, pp. 1702–1711, 2023.
[34] B. Pang, W. Dai, T. Ra, and K. H. Low, “A concept of airspace configuration and operational rules for UAS in current airspace,” in
2020 AIAA/IEEE 39th Digital Avionics Systems Conference (DASC), San
Antonio, TX, USA, 2020.
[35] X. He, F. He, L. Li, L. Zhang, and G. Xiao, “A route network planning method for urban air delivery,” Transportation Research Part E: Logistics and Transportation Review, vol. 166, p. 102872, 2022.
[36] M. F. B. Mohamed Salleh, C. Wanchao, Z. Wang, S. Huang, D. Y. Tan, T. Huang, and K. H. Low, “Preliminary concept of adaptive urban airspace management for unmanned aircraft operations,” in 2018 AIAA Information Systems-AIAA Infotech@ Aerospace, Kissimmee, Florida, USA, 2018.
[37] B. Li, H. Zhang, L. Zhang, D. Feng, and Y. Fei, “Research on path planning and evaluation method of urban logistics UAV,” in 2021 3rd International Academic Exchange Conference on Science and Technology Innovation (IAECST), Guangzhou, China, 2021.
[38] Q. Zhou and G. Liu, “UAV path planning based on the combination of A-star algorithm and RRT-star algorithm,” in 2022 IEEE International Conference on Unmanned Systems (ICUS), Guangzhou, China, 2022.
[39] Z. Yu, Z. Si, X. Li, D. Wang, and H. Song, “A novel hybrid particle swarm optimization algorithm for path planning of UAVs,” IEEE Internet Things J, vol. 9, no. 22, pp. 22 547–22 558, 2022.
[40] V. Roberge, M. Tarbouchi, and G. Labonté, “Comparison of parallel genetic algorithm and particle swarm optimization for real-time UAV path planning,” IEEE Trans. Ind. Inf, vol. 9, no. 1, pp. 132–141, 2012.
[41] H. Zhang, X. Gan, S. Li, and Z. Chen, “UAV safe route planning based on PSO-BAS algorithm,” J. Syst. Eng. Electron, vol. 33, no. 5, pp. 1151–
1160, 2022.
[42] C. Rhodes, C. Liu, and W.-H. Chen, “Autonomous source term estimation in unknown environments: From a dual control concept to UAV deploy- ment,” IEEE Rob. Autom. Lett, vol. 7, no. 2, pp. 2274–2281, 2022.
[43] J. Chang, N. Dong, D. Li, W. H. Ip, and K. L. Yung, “Skeleton extraction and greedy-algorithm-based path planning and its application in UAV trajectory tracking,” IEEE Trans. Aerosp. Electron. Syst, vol. 58, no. 6, pp. 4953–4964, 2022.
[44] N. Wen, L. Zhao, X. Su, and P. Ma, “UAV online path planning algorithm in a low altitude dangerous environment,” IEEE/CAA J. Autom. Sin, vol. 2, no. 2, pp. 173–185, 2015.
[45] R. Hoffman and J. Prete, “Principles of airspace tube design for dynamic airspace configuration,” in The 26th Congress of ICAS and 8th AIAA ATIO, Anchorage, Alaska, USA, 2008.
[46] E. Sunil, J. Hoekstra, J. Ellerbroek, F. Bussink, A. Vidosavljevic, D. Delahaye, and R. Aalmoes, “The influence of traffic structure on airspace capacity,” in 7th International Conference on Research in Air Transportation, vol. 4, Philadelphia, Pennsylvania, USA, 2016.
[47] A. R. Soltani, H. Tawfik, J. Y. Goulermas, and T. Fernando, “Path planning in construction sites: performance evaluation of the Dijkstra, A, and GA search algorithms,” Adv. Eng. Inf, vol. 16, no. 4, pp. 291–303, 2002.
[48] J. Yu, X. Dong, Q. Li, J. Lü, and Z. Ren, “Adaptive practical optimal time-varying formation tracking control for disturbed high-order multi- agent systems,” IEEE Trans. Circuits Syst. I Regul. Pap, vol. 69, no. 6, pp. 2567–2578, 2022.
[49] L. Dong, J. Yan, X. Yuan, H. He, and C. Sun, “Functional nonlinear model predictive control based on adaptive dynamic programming,” IEEE Trans. Cybern, vol. 49, no. 12, pp. 4206–4218, 2019.
APPA-3D: an autonomous 3D path planning algorithm for UAVs in unknown complex environments
Introduction
Unmanned Aerial Vehicles (UAVs) are widely used in a variety of scenarios due to their abilities of high flexibility, high productivity, ease of maneuverability, and adapting to hazardous environments. The increasing complexity of flight environments requires UAVs to have the ability to interact with highly dynamic and strongly real-time space operating environments, which put forward new demands for UAVs’ autonomy and safety. UAVs detect and determine whether there is a potential conflict in the future period through the sensors so that they can maintain a certain safe distance from the dynamic/static obstacles in the airspace, and thus plan an ideal flight path from the starting point to the target point and avoid conflicts.
Unlike civil aircraft, UAVs usually perform tasks in lower airspace. There are many static obstacles in lower airspace such as buildings, trees, and dynamic aircraft. Flight conflict is a state when the distance between two aircraft in the direction of horizontal, longitudinal, or vertical is less than a specific interval resulting in the aircraft being at risk1. UAVs are required to have autonomous environment sensing, collision threat estimation, avoidance path planning, and maneuver control. These abilities are referred to as Sense And Avoid (SAA). Airspace environment sensing in UAV SAA refers to the detection and acquisition of various static/moving, cooperative/non-cooperative targets in the flying space, based on the onboard sensors or data links carried by the UAV, and evaluating the environmental situation and the degree of collision threat2. As shown in Fig. 1, SAA is an important safety guarantee for future UAV airspace integration applications and is also an important sign of autonomy and intelligence of UAVs3.
For UAVs, the ability of SAA is extremely important. The ability of path planning in the avoidance function of UAVs is an important foundation for the basis for them to complete the flight task. Complex flight environments put forward higher demands for path planning algorithms of UAVs, thus the research in autonomous obstacle avoidance path planning algorithms for UAVs is necessary.
It has to find the optimal flight path from the initial location to the target location under the constraints of environmental factors such as terrain, weather, threats, and flight performance of autonomous path planning for UAVs. Significantly, the optimal path does not always mean the shortest path or a straight line between two locations; instead, the UAV aims to find a safe path under limited power and flight task. There are a lot of UAV path planning algorithms, such as the Voronoi diagram algorithm, Rapidly-exploring Random Tree (RRT) algorithm, A* algorithm, etc. However, these algorithms cannot deal with dynamic environments effectively because they require global environmental information to calculate the optimal result. Once the environment changes, the original results will fail. Furthermore, the process of recalculating the optimal results is too slow for real-time operations because of the large number of calculations required. The above algorithms may still be effective if the obstacle is moving slowly. But when moving faster, the movement of the surrounding vehicles may cannot be predicted thus result in a collision. These shortcomings limit the application of the above algorithms to UAVs in real, dynamic environments.
To address these shortcomings, reinforcement learning algorithms are applied to the path planning process. Reinforcement learning (RL) is a branch of machine learning. UAVs can learn through continuous interaction with the environment, using training and learning to master the environment gradually, and optimize the state-behavior continuously to obtain the optimal strategy through the feedback (rewards) given by the environment, which is closer to the human learning process.
Compared with traditional algorithms, RL performs better when the environment is unknown and dynamic. Moreover, the inference speed and generalization of RL have advantages in real-time decision-making tasks. Therefore, the path planning algorithm based on RL has certain advantages in solving the UAV path planning problem in unknown and dynamic environments.
This paper considers the real-time and location limitation characteristics of path planning and refers to the existing research on UAV path planning problems and collision avoidance strategies for various stationary/motion threats. An autonomous collision-free path planning algorithm for UAVs in unknown complex 3D environments (APPA-3D) is proposed. Thus, UAVs can perform tasks with APPA-3D more safely and efficiently in complex flight environments. Firstly, the UAV spherical safety envelope is designed to research the anti-collision avoidance strategy, which will be used as an action plan for UAVs to realize dynamic obstacle avoidance. Secondly, we assume that the environment model when path planning is unknown, so the UAV needs to have the ability to learn and adjust flight state intelligently according to its surroundings. In this paper, the traditional model-free RL algorithm is improved to reduce the complexity of the algorithm and adapt to the demands of UAV path planning in an unknown complex 3D environment. It takes into account the search efficiency while guaranteeing the optimal search path.
Compared with the existing research, the innovative work of this paper mainly manifests in the following several aspects:
Based on the UAV environment sensing capability, a collision safety envelope is designed, and the anti-collision control strategy is studied concerning the Near Mid Air Collision (NMAC) rules for civil airliners and the International Regulations for Preventing Collisions at Sea (COLREGS). It provides a theoretical basis for UAVs to carry out collision detection and avoidance schemes, which can detect and avoid dynamic threats effectively in the flight environment.
To address the difficulty of convergence of traditional algorithms in solving 3D path planning. The artificial potential field method (APF) is used to optimize the mechanism of reward function generation in RL. The optimized algorithm can output the dynamic reward function by combining the actual flight environment information. Thus, the problems of path planning convergence difficulty, unreachable target point and model stop learning in high dimensional space caused by sparse reward function are solved.
Aiming at the "exploration-exploitation dilemma" of RL in the path planning process of UAVs, an RL action exploration strategy based on action selection probability is proposed. The strategy dynamically adjusts the action selection strategy by combining the size of the value function in different states, thus solving the RL exploration-exploitation problem and improving the efficiency of path search.
The rest of the paper is organized as follows: Section "Related research on UAV path planning" introduces the research status of UAV path planning; an anti-collision control strategy for UAVs is designed in Section "UAV anti-collision control strategy"; an Autonomous collision-free path planning algorithm is proposed in Section "Design of autonomous collision-free path planning algorithm for UAVs"; simulation experiment design and result analysis are presented in Section "Experiment and results"; the paper is summarized in Section "Conclusion".
Related research on UAV path planning
Autonomous mobile robots (AMRs) has attracted more and more attention due to their practicality and potential uses in the modern world4. AMRs is widely used in different fields, such as agricultural production5,6, unmanned underwater vehicles (AUVs)7,8, automated guided vehicles (AGVs)9, autonomous cleaning robots10, industrial robots11,12, etc. The similarity of the above studies is that they are all need 3D path planning algorithms. Path planning is one of the most important tasks in AMR navigation since it demands the robot to identify the best route based on desired performance criteria such as safety margin, shortest time, and energy consumption. As an important part of AMRs, with the popularization of consumer-grade UAVs, the research on path planning of UAVs has become a hot topic.
UAV path planning refers to the formulation of the optimal flight path from the initial location to the target location, considering environmental factors such as terrain, meteorology, threats, and their flight performance constraints The aim is to improve the reliability and safety of UAVs while ensuring the efficiency of their task execution.
A lot of research has been done on the UAV path planning problem. Sampling-based path planning algorithms are widely used in UAV path planning due to their simplicity, intuitiveness, and ease of implementation. A simple sampling-based path planning algorithm is the Voronoi diagram algorithm13. The Voronoi diagram algorithm transforms the complex problem of searching for a trajectory in a spatial region into a simple search problem with a weighted diagram. However, the Voronoi diagram algorithm is only suitable for solving 2D path planning problems. 2D path planning divides the flight environment into passable and impassable areas through "rasterization" processing, and then route planning is performed on the processed map. The algorithm is easy to implement and is more intuitive and feasible, but it is difficult to consider terrain following, terrain avoidance, and threat avoidance simultaneously. Therefore, it is necessary to consider the real sense of 3D route planning with real-time and effective requirements to solve the UAV path planning problem in real scenarios. Another intuitive algorithm is the Rapidly exploring Random Tree (RRT)14. RRT can quickly and efficiently search in the smallest possible space, avoiding the need to model the space, and can effectively solve motion planning problems with high-dimensional spaces and complex constraints. However, it is less repeatable and the planned paths are often far from the shortest path.
In node-based path planning algorithms, Dijkstra's algorithm searches for the shortest path by cyclic traversal15, However, as the complexity of the flight map increases and the number of nodes increases, Dijkstra's algorithm suffers from too low execution efficiency. Reference16 designed the solution model of the "Dijkstra -based route planning method", which simplifies the search path, reduces the calculation amount, and improves the execution efficiency through the optimization of correction strategies, correction schemes, and O-D Adjacency matrix processing methods, thereby improving the traditional Dijkstra algorithm. The A* algorithm is a classical and commonly used heuristic search algorithm17. The A* algorithm guides the search through heuristic information to achieve the purpose of reducing the search range and improving the computational speed and can obtain real-time feasible paths. The A* algorithm is well-established in the field of path search in 2D environments18. If it is directly applied to a 3D environment, the problem of exponential rise in computing data and increase in computing time, which leads to slow search efficiency, needs to be improved. Reference19 proposes a model-constrained A * -based three-dimensional trajectory planning for unmanned aerial vehicles. By optimizing the cost function of the traditional A * and selecting extension nodes by controlling the value of the coefficient, the search efficiency of the algorithm is improved. Reference20 proposes a model-constrained A * -based three-dimensional trajectory planning for unmanned aerial vehicles. By optimizing the cost function of the traditional A * and selecting extension nodes by controlling the value of the coefficient, the search efficiency of the is improved.
Computational intelligence (CI) algorithms can provide solutions to NP-hard problems with many variables. CI algorithms are a group of nature-inspired methods, which have been raised as a solution for these problems. They can address complex real-world scenarios that algorithms. Genetic Algorithm (GA)21 is an adaptive global optimization probabilistic search algorithm developed by simulating the genetic and evolutionary processes of organisms in the natural environment. However, the GA algorithm is time-consuming and generally not suitable for real-time planning. Reference22 proposes an improved adaptive GA that adaptively adjusts the probabilities of crossover and genetic operators in a nonlinear manner, enabling the generation of more optimal individuals during the evolution process and obtaining the global optimal solution. Simulation results show that the improved adaptive GA enhances the local search capability of the genetic algorithm, improves the planning efficiency, and can accomplish the UAV path planning task. Particle Swarm Optimization (PSO)23 is an evolutionary computational method based on group intelligence. The biggest advantage of PSO is its simplicity, fast operation speed, and short convergence time. However, in the face of high-dimensional complex problems, PSOs often encounter the drawbacks of premature convergence and poor convergence performance, which cannot guarantee convergence to the optimal point. In recent years, the grey wolf optimization (GWO) algorithm has been widely used in various fields24. The while optimizer (WOA)25 is a GWO-based method because of the success of GWO. Reference26 proposes a parallel PSO and enhanced sparrow search algorithm (ESSA) for unmanned aerial vehicle path planning. In the ESSA, the random jump of the producer’s position is strengthened to guarantee the global search ability. Ni and Wu et al.27 proposes an improved dynamic bioinspired neural network (BINN) to solve the AUV real-time path planning problem. A virtual target is proposed in the path planning method to ensure that the AUV can move to the real target effectively and avoid big-size obstacles automatically. Furthermore, a target attractor concept is introduced to improve the computing efficiency of neural activities. Ni and Yang28 studied the heterogeneous AUV cooperative hunting problem and proposed a novel spinal neural system-based approach. The presented algorithms not only accomplishes the search task but also maintains a stable formation without obstacle collisions. These methods provide some new ideas for the study of UAV path planning in this paper.
Real-time and autonomy in complex flight environments are important indicators for measuring different path-planning algorithms. In the above algorithms, the sampling-based path planning algorithms reduce the traversal search space by sampling, sacrificing the optimality of paths in exchange for a shorter computation time. As the size of the environment increases, the number of operation iterations increases dramatically, making it difficult to achieve simultaneous optimization accuracy and optimal paths in 3D complex environments. Node-based path planning algorithms can obtain the optimal path between the start and endpoints. However, as the environment expands, the dimensionality increases and the number of search nodes increases, the computational size of these algorithms will increase dramatically. Intelligent biomimetic algorithms optimize paths in a mutation-like manner, which can better handle unstructured constraints in complex scenarios. However, its variational solving process requires a long iteration period and cannot be adapted to path planning in dynamic environments29.
In response to the limitations of the traditional algorithms mentioned above, a new feasible solution is to update the distance information between the UAVs and the obstacles and target points in real-time and feed it back to the UAV, as well as to make real-time adjustments to its flight status and maneuvers30. Reinforcement learning (RL)is a branch of machine learning. The UAVs and the flight environment are modeled using Markov Decision Process (MDP), then the UAV chooses the optimal action to maximize the cumulative reward31. UAVs can learn through continuous interaction with the environment, using training and learning to help UAVs gradually master the environment, and continuously optimize the state-behavior to obtain the optimal strategy through the feedback (rewards) given by the environment, which is closer to the human learning process.
In the face of the problem that the environment model is unknown and the transfer probability and value function are difficult to determine, the RL algorithm of interactive learning with the environment to obtain the optimal strategy needs to be a model-free RL algorithm. The Q-Learning (QL) algorithm is one of the most commonly used model-free RL algorithms and has been widely applied to solve path-planning problems. Reference32 proposes a Dynamic Fast Q-Learning (DFQL) algorithm to solve the path planning problem of USV in partially known marine environments, DFQL algorithm combines Q-Learning with an Artificial Potential Field (APF) to initialize the Q-table and provides USV with a priori knowledge from the environment. Reference33 introduces an Improved Q-Learning (IQL) with three modifications. First, add a distance metric to QL to guide the agent toward the target. Second, modify the Q function of QL to overcome dead ends more effectively. Finally, introduce the concept of virtual goal in QL to bypass the dead end. Reference34 proposed a multi-strategy Cuckoo search based on RL. Reference35 uses potential field information to simply initialize the Q-value table, giving it certain basic guidance for the target point. Reference36 proposes a QL algorithm based on neural networks, which uses Radial Basis Function (RBF) networks to approximate the action value function of the QL algorithm.
All in all, RL takes rewards from exploring the environment as training data by imitating the learning process of human beings and trains itself without requiring preset training data. The path planning algorithm of UAV based on RL senses the state information of obstacles in the environment continuously and inputs the information into the algorithm, The optimal collision-free path can be obtained by adjusting the flight state of the UAV through RL, which can solve the problems of poor real-time and long planning time of traditional trajectory planning.
However, in practice, due to the complexity of the flight environment, the traditional RL algorithms do not run well in complex scenarios. More concretely, the memory size of a Q-table increases exponentially as the dimensionality of the state space or action space associated with the environment increases37; The slow convergence caused by dimension explosion will lead to disastrous consequences in path planning, thus limiting the performance of RL in practice; The sparse reward function of the traditional RL algorithm will lead to algorithm convergence difficulties, resulting in the model stops learning and cannot improve; The algorithm faces the "exploration–exploitation dilemma" because it needs to consider both exploration and exploitation in action selection38. Therefore, the RL algorithm needs to be improved and optimized before it is used to solve the UAV path planning problem.
UAV anti-collision control strategy
UAV spherical safety envelope
UAVs are unable to obtain complete priori information about the environment during the flight, and can only obtain the information within a certain range centered on themselves through various onboard sensors such as Light Detection And Ranging (LiDAR), and vision sensors. The maximum distance that the sensors of a UAV can detect is defined as \({D}_{max}\). This paper constructs a spherical safety envelope for UAVs The spherical security envelope is centered at the centroid position of the UAV, which is the demarcation of the threat that the UAV can avoid. It can be used to calculate the action reward of the UAV during RL, and act as an event-triggered mechanism for mandatory UAV anti-collision avoidance strategies. As is shown in Fig. 2, the thresholds of the safety zone named SZ) is \({D}_{max}\); the thresholds of the collision avoidance zone (named CZ) and the mandatory collision avoidance zone (named MZ) are represented by \({D}_{cz}\) and \({D}_{mz}\), respectively. When the obstacle is in SZ, there is no collision risk between the UAV and the obstacles; when the obstacle is in CZ, the UAV needs to conduct a collision warning and be aware that the obstacle may enter the MZ; when the obstacle is in MZ, the anti-collision avoidance strategy will be triggered to ensure safety.
UAV anti-collision avoidance strategies
Before applying APPA-3D to solve the UAV path planning problem, an anti-collision avoidance strategy should be designed. The purpose is to adjust the UAV's flight status such as direction or speed in response to dynamic obstacles (such as other vehicles in the airspace, birds, etc.) to achieve obstacle avoidance. The design of the anti-collision avoidance strategy refers to the method of setting up collision zones in (NMAC) and (COLREGS).
When a dynamic obstacle enters a UAV's MZ, a collision avoidance strategy will be triggered to reduce the risk of collision until the distance between the UAV and the obstacle is greater than \({D}_{mz}\). According to the rules of NMAC, we divide the possible conflict scenarios into flight path opposing conflict、pursuit conflict, and cross conflict. The relative position of the UAV to the dynamic obstacle is shown in Fig. 3.
In Fig. 3, when the flight path of the dynamic obstacle is in the same straight line as the UAV, the two are about to have an opposing conflict or pursuit conflict, and their relative positions are schematically shown in Fig. 3A,B. The vertical direction vector \({f}_{1}\) is added to the direction vector \(f\) of the connection between the UAV and the obstacle. The UAV flies along the direction of merging vector \(F\) of vectors \(f\) and \({f}_{1}\) until it avoids or overtakes an obstacle.
When the flight path of the dynamic obstacle is in the same straight line as the UAV, the two flight paths cross and conflict, and their relative positions are shown in Fig. 3C. Vector \(F\) is the combined vector direction of vector \(f\) and vector \({f}_{1}\). Vector \({f}_{1}\) is opposite to the direction of obstacle movement \(v\). The UAV flies along the merging vector \(F\) to avoid the obstacle.
Based on the different collision scenarios generated by the relative positions of the UAV and dynamic obstacles, four corresponding anti-collision avoidance strategies are designed, as shown in Fig. 4.
In Fig. 4A, there is a risk of opposing conflict between the dynamic obstacle and the UAV. Similar to the method shown in Fig. 3A, the UAV will fly along the merging vector \(\overrightarrow{F}\), to avoid obstacles. The flight paths of the UAV and the dynamic obstacle are shown in Fig. 4A.
In Fig. 4B,C, there is a risk of cross-conflict between dynamic obstacles and UAVs. Similar to the method shown in Fig. 3C, the UAV will fly along the merging vector direction \(\overrightarrow{F}\) and pass behind the moving direction of the dynamic obstacle, thus the UAV can avoid the dynamic obstacle successfully with the shortest avoidance path. The flight paths of the UAV and the dynamic obstacle are shown in Fig. 4B,C.
In Fig. 4D, dynamic obstacles are in the UAV's path of travel and moving at a speed less than the UAV. There is a risk of pursuit and conflict between the dynamic obstacles and the UAV. Similar to the method shown in Fig. 3B, the UAV will fly along the merging vector direction \(\overrightarrow{F}\) to complete the overtaking of the dynamic obstacle. The flight paths of the UAV and the dynamic obstacle are shown in Fig. 4D.
Design of autonomous collision-free path planning algorithm for UAVs
The basic framework of RL is shown in Fig. 5.
Essentially, RL is the use of the Agent to interact with the environment constantly, and obtain the optimal value function \({q}^{*}\) for state \(S\), through the feedback (reward) given by the environment to continuously optimize the state-action to obtain the optimal strategy \({\pi }^{*}\). The mathematical formula is expressed as Eq. (1) and Eq. (2):
$$q^{*} \left( {s,\;a} \right) = \mathop {\max }\limits_{\pi } q_{\pi } \left( {s,\;a} \right)$$
(1)
$$\pi^{*} \left( {a|s} \right) = \left\{ {\begin{array}{*{20}c} {1, \;\;\;\;\;\;\;\; a = argmax_{a \in A} q^{*} \left( {s,a} \right)}\\ {0, \;\;\;\;\;\;\;\;\;\; other} \\ \end{array} } \right.$$
(2)
Thus, the problem of finding the optimal strategy translates into finding the largest of the action state value functions produced under all strategies.
RL-based path planning algorithm allows UAVs to learn and gain rewards through constant interaction with the surroundings through trial and error with little knowledge of the environment and is, therefore, suitable for UAV ‘s path planning under complex conditions. The advantage of an RL-based path planning algorithm is that it can realize path planning in the absence of a priori information about the environment and is highly searchable, but it suffers from the problem of reward sparsity39, which can cause convergence difficulties in high-dimensional spaces.
APPA-3D first combines the principle of the APF method and designs an adaptive reward function. Dynamic rewards are generated in real time by judging the effectiveness of UAV movements with environmental information. Secondly, to address the "exploration-utilization dilemma" of RL in the UAV path planning process, an RL action exploration strategy based on action selection probability is proposed. The strategy dynamically adjusts the action selection strategy by combining the size of the value function in different states, to solve the exploration-utilization problem of RL and improve the efficiency of path search.
Virtual force generation for UAV based on APF
The basic idea of path planning with the APF40 is to design the motion of an object in its surroundings as the motion of an abstract artificial gravitational field. The target point has "gravitational force" on the object, while the obstacle has "repulsive force" on the object, and the motion of the object is controlled by the net force.
The current position of the UAV is denoted as \(X=\left(x,y,z\right)\); the position of the target point is denoted as \({X}_{g}=\left({x}_{g},{y}_{g},{z}_{g}\right)\); and the position of the start point is denoted as \({X}_{0}=\left({x}_{0},{y}_{0},{z}_{0}\right)\). The gravitational potential field function is defined as Eq. (3):
$$U_{att} = \frac{1}{2}kD_{goal}^{2}$$
(3)
In Eq. (3), \(k\)> 0 is the gravitational potential field function coefficient constant. The distance from the UAV to the target point is \({D}_{goal}=\Vert X-{X}_{g}\Vert\), and the gravitational force is the negative gradient of the gravitational potential field function, defined as Eq. (4):
$$F_{att} \left( X \right) = - {\triangledown }\left( {U_{att} \left( X \right)} \right) = k\left( {X_{g} - X} \right)$$
(4)
Define the repulsive potential field function as Eq. (5):
$$U_{rep} \left( X \right) = \left\{ {\begin{array}{*{20}c} {\frac{1}{2}m\left( {\frac{1}{{D_{barrier} }} - \frac{1}{{\rho_{0} }}} \right)^{2} } & {D_{goal} \le \rho_{0} } \\ 0 & {D_{goal} > \rho_{0} } \\ \end{array} } \right.$$
(5)
In Eq. (5), \(m\)> 0 is a repulsive potential field coefficient constant. The position of the obstacle is \({X}_{b}=\left({x}_{b},{y}_{b},{z}_{b}\right)\). The distance from the UAV to the obstacle is \({D}_{barrier}=\Vert X-{X}_{b}\Vert\). \({\rho }_{0}\) is the maximum range of influence of the obstacle. Define the repulsive force as Eq. (6) and Eq. (7):
$$F_{rep} \left( X \right) = - {\triangledown }\left( {U_{rep} \left( X \right)} \right) = \left\{ {\begin{array}{*{20}c} {m\left( {\frac{1}{{D_{barrier} }} - \frac{1}{{\rho_{0} }}} \right)\frac{1}{{D_{battier}^{2} }}\frac{{\partial D_{barrier} }}{\partial X}} & {D_{goal} \le \rho_{0} } \\ 0 & {D_{goal} > \rho_{0} } \\ \end{array} } \right.$$
(6)
$$\frac{{\partial D_{barrier} }}{\partial X} = \left( {\frac{{\partial D_{barrier} }}{\partial x},\;\frac{{\partial D_{barrier} }}{\partial y},\;\frac{{\partial D_{barrier} }}{\partial z}} \right)$$
(7)
Thus the net force \(F\left(X\right)\) on the UAV is shown in Eq. (8)
$$F\left( X \right) = F_{att} \left( X \right) + F_{rep} \left( X \right)$$
(8)
Design of adaptive reward function
The reward function is used to evaluate the actions of the Agent. In traditional RL algorithms, the Agent can only obtain the positive and negative sparse reward function by reaching the target point or colliding with an obstacle. The model does not receive any feedback until it receives the first reward, which may cause the model to stop learning and fail to improve. This reward function will make the algorithm convergence difficult, and in most states cannot reflect the good or bad of its action choice. he sparse reward function \(R\) is shown in Eq. (9):
$$R = \left\{ {\begin{array}{*{20}c} { - 1,} & {s_{t} = Filure} \\ { + 1,} & {s_{t} = Success} \\ {0,} & {s_{t} = Other} \\ \end{array} } \right.$$
(9)
In Eq. (9), \({s}_{t}=Filure\) means that the UAV collides with an obstacle in state t and receives a negative reward − 1, while \({s}_{t}=Success\) means that the UAV reaches the target point in state t and receives a positive reward + 1. Other states have no reward.
To solve the difficult problem of sparse rewards, in this paper, combined with the artificial potential field algorithm, the gravitational force generated by the target point and the repulsive force generated by the obstacle on the agent are converted into the reward or punishment obtained by the agent after performing the action \({a}_{t}\) in the state \({s}_{t}\). The optimized reward function is shown in Eq. (10):
$$R = \left\{ {\begin{array}{*{20}c} {R_{a} } & {D \ge D_{cz} { }or{ }D_{cz} \le D < D_{max} } \\ {R_{cz} } & {D_{mz} \le D < D_{cz} } \\ {R_{mz} } & {D < D_{mz} } \\ \end{array} } \right.$$
(10)
In Eq. (10), \({R}_{a}\) represents the reward function when the obstacle is within the SZ or when no obstacle is detected. the collision avoidance action reward function is \({R}_{ca}\), and the mandatory collision avoidance action reward function is \({R}_{mz}\).
The Euclidean distance between the starting point of the agent and the target is denoted by \({d}_{max}\), and the Euclidean distance between the current position of the agent and the target is denoted by \({d}_{goal}\). The formula as Eq. (11) and Eq. (12):
$$d_{max} = \parallel X_{0} - X_{g}\parallel$$
(11)
$$d_{goal} = \parallel X - X_{g} \parallel$$
(12)
The hyperbolic tangent function can map all will any real number to (− 1, 1). The hyperbolic tangent function can be written as Eq. (13):
$$\tanh x = \frac{\sinh x}{{\cosh x}} = \frac{{e^{x} - e^{ - x} }}{{e^{x} + e^{ - x} }}$$
(13)
As shown in Fig. 6A, when the obstacle is in the SZ, or no obstacle is detected, the UAV is only affected by the gravitational force \({F}_{att}\) generated by the target point, reward function \({R}_{a}\) is as shown in Eq. (14)
$$R_{a} = \left| {\tanh \left( {d_{max} - d_{goal}^{t} } \right)} \right|\frac{{d_{goal}^{t} - d_{goal}^{t + 1} }}{{\left| {d_{goal}^{t} - d_{goal}^{t + 1} } \right|}}$$
(14)
In Eq. (14): \({d}_{goal}^{t}\) denotes the Euclidean distance between the agent position and the target point position at moment \(t\).
From Eq. (14), it can be seen that after each state change of the agent, if the distance between the agent and the target point under \(t+1\) decreases compared to \(t\) moments, then \({R}_{a}>0\), the agent gets a positive reward at this time, and vice versa, it gets a negative reward, which is consistent with the principle of RL.
As shown in Fig. 6B, when the obstacle is in the CZ, the UAV is affected by the repulsive force \({F}_{rep}\) of the obstacle and the attractive force \({F}_{att}\) of the target point. At this time, the reward function decreases with the increase of the distance between the agent and the obstacle. The reward function \({R}_{ca}\) can be written as Eq. (15):
$$R_{cz} = \left| {\tanh \left( {D_{cz} - d_{barrier}^{t} } \right)} \right|\frac{{d_{barrier}^{t + 1} - d_{barrier}^{t} }}{{\left| {d_{barrier}^{t + 1} - d_{barrier}^{t} } \right|}} + \left| {\tanh \left( {d_{max} - d_{goal}^{t} } \right)} \right|\frac{{d_{goal}^{t} - d_{goal}^{t + 1} }}{{\left| {d_{goal}^{t} - d_{goal}^{t + 1} } \right|}}$$
(15)
where: \({d}_{barrier}^{t}\) denotes the Euclidean distance between the agent position and the obstacle position at moment \(t\).
From Eq. (15), it can be seen that the reward function \({R}_{ca}\) when the obstacle is in the CZ consists of two parts, one is the reward generated by the obstacle to the UAV, if the distance between the UAV and the obstacle under the \(t+1\) moment is reduced compared to the \(t\) moment, then the reward generated by the obstacle to the agent is negative, and vice versa is positive. The other is the reward generated by the target point to the UAV, and the principle is the same as Eq. (5). When the obstacle is in the CZ, the agent accepts the reward function of the obstacle and the target point at the same time, which can solve the defects that the traditional APF method is easy to fall into the local minima and oscillate in the narrow passage, to guide the UAV out of the trap area and move toward the target point smoothly.
As shown in Fig. 6C, when the obstacle is within the MZ, the risk of UAV collision with the obstacle is high. To prevent conflicts, A collision avoidance strategy \({A}_{C}\) is mandatory for the UAV, The reward function \({R}_{ca}\) can be written as Eq. (16):
$$R_{mz} = \left| {\tanh \left( {D_{cz} - d_{barrier}^{t} } \right)} \right|\frac{{d_{barrier}^{t + 1} - d_{barrier}^{t} }}{{\left| {d_{barrier}^{t + 1} - d_{barrier}^{t} } \right|}}$$
(16)
The adaptive reward function is consistent with RL. By converting the reward values of each action-state into continuous value between (− 1, 1), the problem of sparse reward functions is solved. The adaptive reward function solves the problem that traditional reward functions can only earn positive or negative rewards by reaching a target point or colliding with an obstacle, and other actions do not receive any positive or negative feedback. The adaptive reward functions are generated by determining the validity of the executed action and environmental information. Compared to the traditional sparse reward function, the adaptive reward function proposed in this paper combines the good performance of APF to make the reward accumulation process smoother, and can also reflect the relationship between the current state of the UAV and the target state.
Action exploration strategy optimization of reinforcement learning
In the process of constant interaction with the environment, the Agent keeps exploring different states and obtains feedback on different actions. Exploration helps the Agent to obtain feedback through continuous experimentation, and Exploitation is where the Agent refers to the use of existing feedback to choose the best action.
On the one hand, RL obtains more information by exploring more of the unknown action space to search for the global optimal solution, but a large amount of exploration reduces the performance of the algorithm and leads to the phenomenon of non-convergence of the algorithm. On the other hand, too much exploitation will fail to choose the optimal behavior because of the unknown knowledge of the environment. Therefore how to balance exploration and utilization is an important issue for the Agent to continuously learn in interaction.
There is a contradiction between "exploration" and "exploitation ", as the number of attempts is limited, and strengthening one naturally weakens the other. Excessive exploration of the unknown action space can degrade the performance of the algorithm and lead to non-convergence of the algorithm while obtaining more information to search for a globally optimal solution. In contrast, too much exploitation prevents the selection of optimal behavior because of the unknown knowledge of the environment. This is the Exploration—Exploitation dilemma faced by RL. To maximize the accumulation of rewards, a better compromise between exploration and exploitation must be reached.
Action exploration strategies can be categorized into directed and undirected exploration methods. The directed exploration approach reduces the blindness in the pre-exploration phase of action exploration and thus improves the exploration efficiency by introducing a priori knowledge into the action exploration strategy. directed exploration methods, on the other hand, make a compromise between exploration and exploitation by setting parameters, and the usual approaches are the \(\epsilon -greedy\) strategy and the Softmax distribution strategy.
The \(\epsilon -greedy\) strategy usually sets a parameter \(\epsilon\) to select the current optimal action with a probability of \(\left(1-\epsilon \right)\), and randomly selects among all the actions with a probability of \(\epsilon\), which is represented by Eq. (17):
$$a = \left\{ {\begin{array}{*{20}l} {Actions \;selected \;with \;uniform \;probability\; in\; A} \hfill & {P = \varepsilon } \hfill \\ {a = argmax_{a \in A} Q\left( {s,\;a} \right)} \hfill & {P = 1 - \varepsilon } \hfill \\ \end{array} } \right.$$
(17)
In Eq. (17), When \(\varepsilon\) is 0, the \(\epsilon -greedy\) strategy is transformed into a greedy strategy, and the degree of exploration gradually increases as \(\varepsilon\) is gradually increased from 0 to 1; when \(\varepsilon\) is 1, the \(\epsilon -greedy\) strategy is transformed into a randomized choice action. Although the \(\epsilon -greedy\) strategy solves the problem between exploration and exploitation to a certain extent, the problem of exploration and exploitation still exists because the parameter \(\epsilon\) is fixed and there are problems such as the difficulty of setting the parameter \(\epsilon\), and the lack of differentiation between non-optimal actions.
The Softmax distribution strategy makes a tradeoff between exploration and exploitation based on the average reward of currently known actions. If the average rewards of the maneuvers are comparable, the probability of selecting each maneuver is also comparable; if the average reward of some maneuvers is significantly higher than that of other maneuvers, the probability of their selection is also significantly higher.
The action assignment for the Softmax distribution strategy is based on the Boltzmann distribution, which is represented by Eq. (18):
$$P\left( {a_{i} |s} \right) = \frac{{e^{{\frac{{Q\left( {s,\;a_{i} } \right)}}{\tau }}} }}{{\mathop \sum \nolimits_{j = 1}^{m} e^{{\frac{{Q\left( {s,\;a_{j} } \right)}}{\tau }}} }}$$
(18)
In Eq. (18), \(Q\left(s,{a}_{j}\right)\) records the average reward of the current action; \(\tau >0\) is called “temperature”, The smaller of \(\tau\), the higher the probability of selecting actions with higher average rewards. When τ tends to 0, Softmax tends to " exploitation only", when τ tends to infinity. Softmax tends to "exploration only".
Both \(\epsilon -greedy\) strategy and the Softmax distribution strategy are iterated in such a way that the action with the largest action-value function has the largest probability of selection. Based on this, this paper proposes a new action selection strategy, the new strategy solves the balance problem between exploration and exploitation by introducing the concept of "action selection probability " and making action preference selection accordingly.
Action selection probability represents the probability value that an Agent chooses to perform an action in a given state. As shown in Eq. (19), the initial value of the action selection probability for a state-action is the inverse of the size of the action set for that state:
$$P\left( {a|s} \right) = \frac{1}{{card\left( {A_{s} } \right)}}$$
(19)
In Eq. (19), \(card\left({A}_{s}\right)\) denotes the number of actions in the action set \({A}_{s}\) in state \(s\).
The action selection probability is dynamically adjusted as the size of the value function of the action changes. During the RL process, Agent in state \(s\), selects action \(A\) based on the size of the action selection probability value, and after executing the action, Agent obtains the reward \(R\) and enters state \({S}^{\mathrm{^{\prime}}}\) and selects the action \({A}^{\mathrm{^{\prime}}}\) with the largest value function to update the value function. Subsequently, the value function for each action in state \(s\) is is divided into two parts according to the size of the value: The largest value function is the first part; the rest is the second part. Reduce the probability values of each action in the second part by half and add them evenly to the first part.
The Agent updates the action selection probability after completing an action, according to the size of the state action value function. The update rule is as Eq. (20):
$$\left\{ {\begin{array}{*{20}l} {P\left( {a_{i} |s} \right) + \mathop \sum \limits_{{j = 1{}a_{j} \notin A^{*} \left( s \right)}}^{n} \frac{{P\left( {a_{j} |s} \right)}}{m}} \hfill & {a_{i} \in A^{*} \left( s \right) = \arg \max_{a \in A} Q^{*} \left( {s,\;a} \right)} \hfill \\ {P\left( {a_{j} |s} \right)\left( {1 - \frac{1}{m}} \right)} \hfill & {other} \hfill \\ \end{array} } \right.$$
(20)
In Eq. (20): \(m\) is the rate of change, which represents the rate of change of the action probability; \({A}^{*}\left(s\right)\) is the set of actions with the largest value function, \({a}_{i}\) is the action of the set \({A}^{*}\left(s\right)\), and \({a}_{j}\) is the action with non-maximum value function.
In the initial phase of the algorithm, each action has the same probability of being selected by the Agent, i.e., the action selection probabilities \(P\left(a|s\right)\) are equal, at which point the Agent will randomly select the action.
After an Agent completes the exploration of an action, if this exploration results in \(R<0\), the action selection probability for that action is halved, at which point the probability of other actions being selected increases, so that in the early stages of the exploration the Agent will be more inclined to select actions that have not been performed. If \(R>0\) for this exploration, it indicates that this exploration is a beneficial exploration, which will increase the action selection probability of this action, when the probability of other actions being selected decreases, and therefore the Agent tends to select this action more often; However, there is still a probability of exploration for other actions, thus reducing the risk of action exploration falling into a local optimum.
The pseudo-code for APPA-3D is shown in Algorithm 1:
Experiment and results
To verify the feasibility of an autonomous path planning algorithm in complex 3D environments (APPA-3D) for UAVs, this paper selects real environment maps to conduct simulation experiments. The UAV's range of action is limited to the map, and if the UAV moves outside the range of the map or above the low altitude limit altitude, it is determined that a collision has occurred. The starting point for UAV path planning is represented by a black dot, and the target point is represented by a red dot. The maximum flight altitude is 1 km above the peak line, and the no-fly zone is indicated by a green cylinder. The UAV needs to avoid mountains and no-fly zones to fly from the starting point to the target point.
UAV anti-collision avoidance strategies experiments
The anti-collision avoidance strategies experiments were designed to verify whether APPA-3D can achieve anti-collision avoidance strategies while implementing path planning. Figures 7, 8 and 9 are simulation experimental diagrams of anti-collision avoidance strategies for UAVs.
As shown in Fig. 7, in the opposing conflict avoidance simulation, the intrusion direction of the dynamic obstacle is set to be directly opposite the movement direction of the UAV. When a dynamic obstacle is detected, the UAV chooses to turn right to avoid the dynamic obstacle according to the anti-collision avoidance strategy. The reward function is recalculated after finishing the anti-collision avoidance strategy and guiding the UAV to continue flying toward the target point.
As shown in Fig. 8, in the cross-conflict avoidance simulation, dynamic obstacles invade from the left and right sides of the UAV's flight direction. According to the anti-collision avoidance strategy, when the UAV detects a dynamic obstacle and chooses to pass behind the moving direction of the dynamic obstacle, it can ensure that the UAV and the dynamic obstacle are avoided successfully and the avoidance path is the shortest. The reward function is recalculated after finishing the anti-collision avoidance strategy and guiding the UAV to continue flying toward the target point.
As shown in Fig. 9, in the pursuit conflict avoidance simulation, the flight direction of the dynamic obstacle is the same as the UAV flight direction. Referring to the anti-collision avoidance strategy, when the UAV detects a dynamic obstacle, the UAV chooses to complete the overtake from the right side of the dynamic obstacle's direction of motion, which ensures that the UAV can successfully overtake the dynamic obstacle with the shortest overtake avoidance path; The reward function is recalculated after finishing anti-collision avoidance strategy and guiding the UAV to continue flying towards the target point.
Multi-obstacle path planning and collision avoidance verification
To verify the performance of the APPA-3D, this paper randomly generates 3, 6, and 10 different moving and static obstacles in the same simulation environment and conducts three sets of randomized experiments each. The 3D view of APPA-3D is exhibited in this paper, as shown in Fig. 10.
The 3D view of the paths planned by APPA-3D shows that the flight paths of the UAVs are feasible in nine different scenarios. The distance between the UAV and the obstacle is well-maintained in complex terrain. This further demonstrates that APPA-3D can help the UAV to plan a path that is both short and safe at the same time.
This paper calculates four parameters: UAV path planning time, planned path length, number of planned path points, and planned path ground projection length in 9 scenarios, the average values of the four parameters are shown in Table 1.
Comparative experiments
To verify the enhancement effect of the adaptive reward function and the new action selection strategy proposed in this paper, two sets of ablation experiments were conducted firstly before conducting the comparison experiments.
The first set of ablation experiments is to verify the enhancement effect of the new adaptive reward function proposed in this paper, and the experimental results are shown in Fig. 11:
The yellow path in Fig. 11 represents the UAV flight path under the sparse reward function, and the blue path represents the flight path under the adaptive reward function proposed in this paper. Figure 11 clearly shows that the performance of UAV path planning based on sparse reward function is poor in complex 3D environments. This is because under sparse reward function, it can only obtain positive and negative reward when reaching the target point or colliding with obstacles, and other actions will not get any positive or negative feedback. So the UAV is random flight blindly, unable to find the correct flight direction in this way. Compared with the sparse reward function, the adaptive reward function we proposed combines the good performance of APF to make the reward accumulation process smoother and can also reflect the relationship between the current state and the target state of the UAV.
To verify the improvement effect of the new action selection strategy proposed in this paper, the second set of ablation experiments was set up. The experiments were analyzed using the \(\epsilon -greedy\) strategy, Softmax distribution strategy, and the new action selection strategy. All RL algorithms adopt Q-learning algorithm, which excludes the influence of learning algorithm on different exploration strategies.
Tables 2 and 3 show the results of three exploration strategies. To prevent the impact of single data on the experiment, the data in Tables 2 and 3 is the average value obtained after 5 experiments.
The experimental results show that after a period of exploration, three different exploration strategies are able to guide the UAV to the target point. Compared with the other two exploration strategies, the action selection probability we proposed is more advantageous in terms of path planning time and number of path planning points.
To evaluate whether the APPA-3D proposed in this paper has significant advantages over other classical or RL based algorithms, two sets of experiments were utilized to test the ability of the six methods to solve path planning problems under the same conditions. According to the characteristics of algorithms, they can be divided into two categories: classic algorithms (APF, RRT, and A*) and QL-based algorithms (DFQL, IQL, and MEAEO-RL). It should be noted that, to prevent the impact of single data on the experiment, the data in Table 4, 5, 6 and 7 is the average value obtained after 5 experiments.
The experimental results of the first group are displayed in Fig. 12 and Tables 4 and 5:
It can be seen from Fig. 12 that the three classic algorithms perform better than APPA-3D algorithm in the front part of the path. However, the performance of classic algorithms is poor in the latter part of the path, which is caused by their algorithm characteristics. Because sampling-based and search-based characteristics of algorithms respectively, it is hard to generate smooth and optimal paths with RRT and A*. Although the path planning time of A* is short, the UAV collided with obstacles unfortunately. The reason for the poor effect of APF is that the obstacle surrounds the destination, and the repulsive force field of the obstacle directly acts on the agent, making it unable to approach the obstacle. The agent can only move in the direction where the gravitational force is greater than the repulsive force.
The results of the second group of experiments are displayed in Fig. 13. It is worth mentioning that DFQL, IQL, MEAEO-R, and APPA-3D are all optimized based on traditional RL algorithms. The simulation results are shown in Fig. 13, Table 6 and Table 7.
Experimental results clearly show that APPA-3D can reach the destination with the shortest distance and time. In the initial phase of path planning, APPA-3D is not very different from other algorithms, and all four algorithms can help the UAV plan a relatively high-quality flight path quickly. While in the middle and later stages of path planning, the differences between APPA-3D and the other three compared algorithms can be seen clearly, especially when facing multi-dynamic obstacles. Because RL algorithm assigns a probability to each possible action and selects the action based on these probabilities, path planning algorithms based on RL often fall into the dilemma of exploration–exploitation when facing complex environments.
To solve this problem, the APPA-3D algorithm proposes a new action selection strategy. This strategy solves the balance problem between exploration and exploitation by introducing the concept of action selection probability and making action preference selection accordingly.
The Fig. 14 presents the loss function used to observe the convergence behavior over iterations of all algorithms. It can be seen that after about 130 iterations, the loss function begins to stabilize. The rapid convergence of value loss also shows that the APPA-3D is more accurate, which is a good performance and means that the agents won’t fall into a local optimum. The algorithms compared requires more iteration to complete convergence. This is because they use \(\epsilon -greedy\) strategy or Softmax distribution strategy as an action exploration strategy of reinforcement learning. And their performance is consistent with the results of the second set of ablation experiments.
In conclusion, APPA-3D is far better than the compared algorithms in the 3D UAV path planning optimization problem. This is because APPA-3D dynamically adjusts the action selection strategy by combining the size of the value function in different states, thus solving the problem of exploration-utilization of RL and improving the efficiency of path search.
Conclusion
The path planning problem in unknown environments is the focus of UAV task planning research and the key to achieving autonomous flight. Therefore, UAVs need to have the ability to autonomous path planning and avoid potential obstacles. In this paper, an autonomous collision-free path planning algorithm for unknown complex 3D environments is proposed. Firstly, based on the environment sensing capability, a UAV collision safety envelope is designed, and the anti-collision control strategy is investigated, which can effectively deal with the collision problem triggered by dynamic obstacles in the flight environment. Secondly, this paper optimizes the traditional RL algorithm. On the one hand, the reward function for RL is optimized by transforming the relationship between the current state of the UAV and the task into a suitable dynamic reward function. The presence of a dynamic reward function allows the UAV to fly toward the target point without getting too close to the obstacles. On the other hand, an RL action exploration strategy based on action selection probability is proposed. The strategy dynamically adjusts the action selection strategy by combining the size of the value function in different states, thus solving the RL exploration-utilization problem and improving the efficiency of path search. To verify the effectiveness of the designed APPA-3D algorithm in the dynamic collision avoidance model, three typical collision experiments were set up, including flight path opposing collision, pursuit collision, and cross collision. The experimental results verify that the APPA-3D can effectively avoid safety threats that may be caused by dynamic obstacles in complex environments according to the designed anti-collision control strategy. Meanwhile, the results of the algorithm testing experiments in nine different scenarios verified that the algorithm still performs well in the face of random and complex flight environments.
APPA-3D demonstrates better performance in path planning performance comparison tests with other classical and novel optimized RL algorithms. The advantages in path planning length and convergence curves again show that APPA-3D can effectively help UAVs solve the path planning problem.
Data availability
The datasets used and analysed during the current study will be available from the corresponding author on reasonable request.
References
Lanicci, J. et al. General aviation weather encounter case studies. Case Stud. 56, 1233 (2012).
Lyu, Y. et al. UAV sense and avoidance: concepts, technologies, and systems (in Chinese). Sci. Sin. Inform. 49, 520–537 (2019).
Li, Y. J., Quan, P., Feng, Y., et al. Multi-source information fusion for sense and avoidance of UAV[C]. Control Conf (IEEE, 2010).
Loganathan, A. & Ahmad, N. S. A systematic review on recent advances in autonomous mobile robot navigation. Eng. Sci. Technol. Int. J. 40, 101343 (2023).
Fasiolo, D. T., Scalera, L., Maset, E. & Gasparetto, A. Towards autonomous mapping in agriculture: A review of supportive technologies for ground robotics. Robot. Auto. Syst. 25, 104514 (2023).
Hameed, I. A., la Cour-Harbo, A. & Osen, O. L. Side-to-side 3D coverage path planning approach for agricultural robots to minimize skip/overlap areas between swaths. Robot. Auton. Syst. 76, 36–45 (2016).
Yan, Z., Yan, J., Wu, Y., Cai, S. & Wang, H. A novel reinforcement learning based tuna swarm optimization algorithm for autonomous underwater vehicle path planning. Math. Comput. Simul. 209, 55–86 (2023).
Hadi, B., Khosravi, A. & Sarhadi, P. Deep reinforcement learning for adaptive path planning and control of an autonomous underwater vehicle. Appl. Ocean Res. 129, 103326 (2022).
Zhong, M., Yang, Y., Dessouky, Y. & Postolache, O. Multi-AGV scheduling for conflict-free path planning in automated container terminals. Comput. Indust. Eng. 142, 106371 (2020).
Do, H. et al. Heat conduction combined grid-based optimization method for reconfigurable pavement sweeping robot path planning. Robot. Autonom. Syst. 152, 104063 (2022).
Wang, X. et al. Adaptive path planning for the gantry welding robot system. J. Manuf. Process. 81, 386–395 (2022).
Cheng, X. et al. An improved RRT-Connect path planning algorithm of robotic arm for automatic sampling of exhaust emission detection in Industry 4.0. J. Indust. Inf. Integr. 33, 100436 (2023).
Pehlivanoglu, Y. V. A new vibrational genetic algorithm enhanced with a Voronoi diagram for path planning of autonomous UAV. Aerosp. Sci. Technol. 16(1), 47–55 (2012).
Guo, J., Xia, W., Xiaoxuan, Hu. & Ma, H. Feedback RRT* algorithm for UAV path planning in a hostile environment. Comput. Ind. Eng. 174, 108771 (2022).
Wang, H., Mao, W. & Eriksson, L. A three-dimensional dijkstra’s algorithm for multi-objective ship voyage optimization. Ocean Eng. 186, 106131 (2019).
Li, Y. Q., Liu, Z. Q., Cheng, N. G., Wang, Y. G. & Zhu, C. L. Path Planning of UAV Under Multi-constraint Conditions. Comput. Eng. Appl. 57(04), 225–230 (2021).
Huang, X. et al. The improved A* obstacle avoidance algorithm for the plant protection UAV with millimeter wave radar and monocular camera data fusion. Rem. Sens. 13(17), 3364 (2021).
Lu, F. Shortest path algorithms: Taxonomy and advance in research. Act a Geodaet Ica Et Cart Ograph. Sin. 03: 269–275 (2001).
Shengyin, W., Teng, L. & Zhu, W. Dynamic path planning using anytime repairing sparse A~* algorithm. Syst. Eng. Electr. 40(12), 2714–2721 (2018).
Zhang, R., Wang, W. & Tian, Z. UAV 3D path planning based on model constrained A* algorithm. Foreign Electr. Meas. Technol. 41(09), 163–169. https://doi.org/10.19652/j.cnki.femt.2203963 (2022).
Shushan, L. et al. 3D track optimization of UAV ( unmanned aerial vehicles) inspection of transmission tower based on GA-SA. Sci. Technol. Eng. 23(6), 2438–2446 (2023).
Zhou, Z. & Chen, P. 3D path planning of UAV based on improved adaptive genetic algorithm. J. Project. Rockets Miss. Guid. 2, 1–7 (2023).
Yang, L. I. U., Zhang, X., Zhang, Y. & Xiangmin, G. Collision free 4D path planning for multiple UAVs based on spatial refined voting mechanism and PSO approach. Chin. J. Aeronaut. 32(6), 1504–1519 (2019).
Jiang, W., Lyu, Y., Li, Y., Guo, Y. & Zhang, W. UAV path planning and collision avoidance in 3D environments based on POMPD and improved grey wolf optimizer. Aeros. Sci. Technol. 121, 107314 (2022).
Sanjoy, C., Sushmita, S. & Apu, K. S. SHADE–WOA: A metaheuristic algorithm for global optimization. Appl. Soft Comput. 113, 107866. https://doi.org/10.1016/j.asoc.2021.107866 (2021).
Wang, Z., Sun, G., Zhou, K. & Zhu, L. A parallel particle swarm optimization and enhanced sparrow search algorithm for unmanned aerial vehicle path planning. Heliyon 9(4), e14784. https://doi.org/10.1016/j.heliyon.2023.e14784 (2023).
Ni, J., Wu, L., Shi, P. & Yang, S. X. A dynamic bioinspired neural network based real-time path planning method for autonomous underwater vehicles. Comput. Intell. Neurosci. 2017, 9269742. https://doi.org/10.1155/2017/9269742 (2017).
Ni, J. et al. An Improved Spinal Neural System-Based Approach for Heterogeneous AUVs Cooperative Hunting. Int. J. Fuzzy Syst. https://doi.org/10.1007/s40815-017-0395-x (2017).
Yang L, Qi JT, Xiao JZ, et al. A literature review of UAV 3D path planning. Proc of the 11th World Congress on Intelligent Control and Automation. (IEEE, 2015).
Yu, X., Zhou, X. & Zhang, Y. Collision-free trajectory generation and tracking for UAVs using markov decision process in a cluttered environment. J. Intell. Robot. Syst. 93, 17–32 (2019).
Feinberg, A. Markov decision processes: discrete stochastic dynamic programming (Martin L. Puterman). SIAM Rev. 38(4), 689–689 (1996).
Hao, B., He, Du. & Yan, Z. A path planning approach for unmanned surface vehicles based on dynamic and fast Q-learning. Ocean Eng. 270, 113632 (2023).
Low, E. S., Ong, P., Low, C. Y. & Omar, R. Modified Q-learning with distance metric and virtual target on path planning of mobile robot. Exp. Syst. Appl. 199, 117191 (2022).
Xiaobing, Yu. & Luo, W. Reinforcement learning-based multi-strategy cuckoo search algorithm for 3D UAV path planning. Exp. Syst. Appl. 63, 119910 (2023).
Gong, M., Xu, H. & Feng, H. Ship local path planning based on improved Q-learning. J Ship Mech 26(06), 824–833 (2022).
Yuliang, W. & Wuyin, J. Intelligent vehicle path planning based on neural network Q-learning algorithm. Fire Control Comm. Control 44(02), 46–49 (2019).
Vanhulsel, M., Janssens, D., Wets, G. & Vanhoof, K. Simulation of sequential data: An enhanced reinforcement learning approach. Exp Syst. Appl 36(4), 45660 (2009).
Zhi-Xiong, X. U. et al. Reward-Based Exploration: Adaptive Control for Deep Reinforcement Learning. IEICE Trans. Inf. Syst. 101(9), 2409–2412. https://doi.org/10.1587/transinf.2018EDL8011 (2018).
Dann, M., Zambetta, F. & Thangarajah, J. Deriving subgoals autonomously to accelerate learning in sparse reward domains. Proc. AAAI Conf Artif. Intell. 33(01), 881–889. https://doi.org/10.1609/aaai.v33i01.3301881 (2019).
Khatib O, Real-time obstacle avoidance for manipulators and mobile robots. Proc. 1985 IEEE International Conf. on Robotics and Automation, St. Louis, pp. 500–505 (1985). https://doi.org/10.1109/ROBOT.1985.1087247.
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher's note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Wang, J., Zhao, Z., Qu, J. et al. APPA-3D: an autonomous 3D path planning algorithm for UAVs in unknown complex environments. Sci Rep 14, 1231 (2024). https://doi.org/10.1038/s41598-024-51286-2
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-024-51286-2
A path planning algorithm for three-dimensional collision avoidance based on potential field and B-spline boundary curve
Get rights and content
Abstract
Path planning is one of the key technologies in unmanned aerial systems. The path-planning algorithm for UAVs in this study incorporates a three-dimensional obstacle model, addressing the limitations of existing research that primarily focuses on the two-dimensional plane. This approach elevates traditional two-dimensional obstacle constraints to a three-dimensional space, fulfilling the requirements for precise obstacle avoidance. Utilizing B-spline curves, an obstacle boundary model is proposed, which, in combination with an improved artificial potential field accounting for localized self-locking oscillations, achieves smooth path planning for obstacle avoidance from the starting point to the destination. The simulation results show the effectiveness of this method in collision-free path planning within three-dimensional environments containing static single or multiple obstacles. At the points of maximum curvature in the two-dimensional coordinate system, the path planned by the proposed algorithm exhibits a smoothness improvement of 68 % and 98 %, respectively, as compared to the traditional artificial potential field algorithm with the equivalent three-dimensional obstacle model and the tangent point method. The proposed algorithm enables drones to achieve precise obstacle avoidance along surfaces, generating smoother collision-free flight paths in a shorter period of time.
Keywords
Three-dimensional path planning
Artificial potential field
B-spline curve
Fibonacci sphere
1. Introduction
1.1. Research background
The emergence of unmanned aerial vehicles (UAVs) is inevitable due to technological advancements and societal progress [1]. The ubiquitous use of UAVs is progressively integrating them into the fabric of everyday life. Due to the diversification of requirements and tasks, a transition from the initial two-dimensional space to a three-dimensional space is imperative for numerous pivotal technologies in the field of UAV path planning and tracking control. Three-dimensional path planning has garnered significant attention and emerged as a focal point of research. Despite significant advancements in previous research, the path planning of drones to achieve more precise, faster, and more stable trajectories for reaching target points in three-dimensional space is still confronted with substantial challenges [2].
1.2. Literature review
The artificial potential field (APF), a classical local path planning algorithm, is a virtual force method proposed by Khatib [3]. It can realize local dynamic obstacle avoidance according to the motion information of obstacles. In comparison to heuristic algorithms such as the A* algorithm [4,5], RRT* [6,7], ant colony algorithm [8], and genetic algorithm [9,10], the APF algorithm possesses the advantages of being fast and straightforward [11]. The fundamental concept is to consider the flight movement of the UAV as motions influenced by a three-dimensional virtual force field. The proposed approach incorporates obstacles in the environment as repulsive force point sources, impeding the UAV's trajectory, while the target point exerts an attractive force to guide its movement. The APF method not only enables avoidance of static obstacles but also allows real-time evasion of dynamic obstacles by leveraging the UAV's onboard sensors to perceive the surrounding flight environment. This capability endows it with the potential for efficient path planning in complex environments [12,13].
In the three-dimensional complex flight environment, the traditional artificial potential field (TAPF) still exhibits several flaws and shortcomings [14]. For instance, the occurrence of the local minimum problem may result in the UAV becoming trapped in a "deadlock" situation failing to reach the intended target point [15]. Extensive research efforts have been devoted to enhancing this problem, including adding quintic polynomial functions [16], positioning risk [17], incorporating a dynamic gravitational constant [18] as well and adopting a spiral potential field [19,20] to alter the stress distribution near the local minimum point. The avoidance issue is effectively addressed by utilizing an enhanced artificial potential field function, which transforms it the heading angle [21], thereby guiding the aircraft towards the target region. Furthermore, the APF method demonstrates remarkable scalability and exhibits robust interaction with its environment. With a multitude of variant functions, it can be flexibly integrated with other algorithms, which could mitigate its inherent limitations effectively [22,23]. This dynamic integration has led to a continuous stream of notable accomplishments. In environments containing static and dynamic obstacles, the bacterial potential field combined with APF can expedite the discovery of the optimal path and reduce the probability of encountering a typical local minimum trap [24]. The shortest path is generated by devising a hybrid algorithm model with the ant colony optimization algorithm, particle swarm optimization algorithm, and A* algorithm in a multi-layer framework [25]. The length of the planned path is effectively reduced by upgrading TAPF to an elliptical potential field and establishing the obstacle boundary [26]. Rao et al. [27] utilized the potential field function to optimize the heuristic function, and the efficiency of identifying the optimal path is enhanced. This integration helps overcome the limitations of traditional methods in global path planning and enhances the performance of global path planning. In addition to single-agent systems, artificial potential fields find extensive application in the field of multi-agent obstacle avoidance path planning [28]. By utilizing an improved artificial potential field as the foundational avoidance algorithm and combining it with a trajectory control algorithm for drone formations, collisions could be effectively prevented between drone formations and obstacles [29].
The geometric shapes of obstacles in three-dimensional path planning are commonly classified based on their projections in the path's vertical plane, which typically includes point-like, linear, planar obstacles, and polygonal obstacles [30]. The shape of the obstacle must be fully considered to achieve accurate obstacle avoidance. Establishing spatial models corresponding to obstacles of different shapes as constraints is conducive to correcting the problem of excessive or insufficient corrections in the process of obstacle avoidance and improving the accuracy of local obstacle avoidance. Zheng et al. [31] decomposed the three-dimensional concave obstacle into multiple parts and approximated it as a convex obstacle. The obstacle avoidance path is generated based on the deformed dynamic system, which can be either linear or non-linear. Yang et al. [32] introduced the concept of the velocity obstacle spherical cap into a three-dimensional obstacle avoidance strategy involving multiple obstacles. Under the constraint that both the robot and the obstacle can take any shape as rigid bodies, Animesh Chakravarthy [33] employed the concept of a collision cone to devise obstacle avoidance strategies. These strategies address the collision problem that arises between an autonomous guided vehicle or autonomous mobile robot and a moving obstacle. Tan et al. [34] introduced collision cones and velocity obstacle cones between mobile robots and obstacles, leading to the design of an enhanced three-dimensional velocity obstacle algorithm, which facilitates obstacle avoidance strategies for multiple drones. The three-dimensional space is decomposed into several stationary or moving polyhedra [35]. By searching for connecting polyhedra between the initial and target polyhedra that satisfy the constraint conditions, collision-free trajectories are obtained. Obstacle modeling is typically approached in one of two ways: simplifying a three-dimensional obstacle to a boundary constraint within a two-dimensional spatial geometry or establishing a collision cone model that defines the no-fly zones.
1.3. Contributions of the work
This paper attempts to make three original contributions and improvements to the current research, as shown in the following:
- 1)
Innovative three-dimensional flight environment. Committed to improving the constraint dimension of spatial obstacles, a novel strategy of replacing spatial obstacles with the Fibonacci sphere generated by the golden ratio is proposed. This approach yields more effective and precise obstacle information, thereby enhancing flight safety.
- 2)
An improved path-planning algorithm. Building upon the foundation of the traditional artificial potential field, this study introduces a local minimum detection mechanism. By dynamically monitoring the speed iteration angle and path iteration step length, the algorithm accelerates the detection of path points approaching local optima. The integration of the optimized speed potential field and repulsive potential field expedites the process of the unmanned aerial vehicle escaping local minima and transitioning into stable flight.
- 3)
Novel obstacle avoidance. With the aim of enhancing obstacle avoidance accuracy, the local obstacle avoidance model is proposed that combines the Fibonacci sphere method with B-spline obstacle boundary curves. The method is based on the development of a Fibonacci sphere obstacle model, which is capable of identifying the accurate unobstructed path and generating smooth planning trajectories.
1.4. Organization of the paper
The algorithm structure and workflow of this paper are primarily composed of several key parts, as depicted in Fig. 1. Initially, the spatial boundaries for flight are defined, and the flight mission needs to be specified. Customizations are made to the size and positions of obstacles within the flight space. Using the proposed approach, an obstacle model is constructed, resulting in the formation of a three-dimensional spatial map of the flight environment. Subsequently, an enhanced artificial potential field algorithm is employed in conjunction with a local obstacle avoidance strategy to perform obstacle path planning for the drone's journey from the starting point to the destination. The rest of the paper is structured as follows: Section 2 provides a brief review of the TAPF method and its drawbacks while introducing an improved three-dimensional velocity potential field model. The B-spline obstacle avoidance strategy for the Fibonacci Sphere obstacle model is introduced in Section 3. Section 4 consists of the simulation results and analysis of obtained results. Finally, the conclusion is given in Section 5.

Fig. 1. The detailed framework of the proposed method.
2. Establishment of the three-dimensional velocity potential field
2.1. Traditional artificial potential field method
The commonly used attractive field function in the traditional artificial potential field method is:(1)where katt is the attractive factor, and ρ(q,qgoal) is the Euclidean distance between the vehicle and the target point.
The repulsive field function is given by:(2)
η is the repulsion factor, ρ(q,qobs) is the Euclidean distance between the aircraft and the obstacle, and ρ0 represents the influence range of the obstacle.
The negative gradient function of the field is the traditional force field formula:(3)(4)
In the TAPF method, the controlled object may experience a scenario where the resultant force of resistance cancels out the attractive force, leading to local oscillation and an inability to escape. Consequently, the object cannot reach the target point to fulfill the specified task.
2.2. Problem assumptions
In this paper, our research primarily focuses on several key objectives: modeling obstacles in three-dimensional space, designing local obstacle avoidance strategies, and improving algorithms. To achieve these objectives, we choose to primarily focus on a specific type of multirotor drone due to its widespread utilization across various applications. Thus, the assumptions and analyses in this study are specifically designed to be consistent with this UAV category. We have formulated assumptions for the following scenarios:
- 1.
The UAV is treated as a point mass capable of flying in three-dimensional space along any angle within a certain range of speeds.
- 2.
The flight environment is static and unaffected by natural weather conditions, and the obstacle model remains constant over time.
- 3.
It is assumed that the UAV's sensors can accurately perceive distance, direction, and velocity information.
- 4.
The UAV's propulsion system is assumed to be ideal, possessing sufficient energy to fly within the constructed environment.
- 5.
Only a single unmanned aerial vehicle is present, and collaboration between multiple UAVs is not considered.
- 6.
It is assumed that discrete waypoints can replace continuous waypoints.
2.3. Improved artificial potential field (IAPF)
The velocity potential field is a branch of APF, which leverages differential information from the position data obtained in APF to derive effective control variables. The present study employs a segmented potential field strategy, and the design enhances the attractive potential field as follows:(5)where katt is the coefficient of attraction, s is the constant coefficient, ρ(q,qgoal) is the Euclidean distance between the drone and the target point, and ρg is the maximum influence range of the attractive potential field. The improved attraction velocity formula can be obtained by taking the first-order differential of the attractive field function.(6)(7)
When the vehicle is outside the range of the attractive potential field, it can maintain a high-speed flight within the safe zone based on its own characteristics. As the distance between the drone and obstacles decreases, the drone will initially enter the repulsive field. At this point, the flight speed gradually decreases under the influence of the repulsive field. This variation in speed helps the vehicle to navigate around obstacles in a stable manner, reducing the adverse effects of inertia. The improved formulas for the repulsion potential field and velocity potential field are as follows:(8)(9)
In the improved repulsion potential field function, a local minimum detection mechanism is incorporated, where m represents the local minimum detection factor, and β denotes the regulatory factor.
The current velocity of vehicle is set as vi, as depicted in Fig. 2. After one iteration, the velocity vector becomes vi+1. When the iteration angle α between vi and vi+1 is below the threshold α0, or the iteration step size is less than the threshold l0, the escape from local minimum mechanism is activated. At this moment, the value of the detection factor m is changed to 1, and the repulsive force potential field function is regulated. Once variable iteration differences are greater than the threshold, the adjustment mechanism concludes, and m returns to 0. The path points continue to iterate according to the improved artificial potential field algorithm.

Fig. 2. Local minimum region.
When the iteration angle α=0, indicating that the aircraft, obstacle, and target point are aligned in a straight line, the resultant force vector of the aircraft will always remain in that straight line, causing waypoints to oscillate back and forth. The offset velocity vve is introduced to change the flight direction. The calculation formula for vve is as follows:(10)where λ is a constant coefficient, and the choice of the positive or negative sign is determined by the velocity direction moving away from the center of the obstacle.
3. Trajectory planning in the static single obstacle ball scenario
3.1. Obstacle model of Fibonacci sphere
Numerous studies have shown that the spherical center or tangent point of an obstacle is often considered to be the equipotential point of repulsion of a vehicle [36]. However, the size of the obstacle cannot be ignored in the actual obstacle avoidance process, especially when it is noticeably larger than the size of the aircraft. The equivalent model of the spherical obstacle is established by utilizing the golden angle method to generate uniformly distributed repulsive point sources on the surface of a sphere.
The Fibonacci sphere (FS) is a deterministic method based on the golden ratio [37], as depicted in Fig. 3. The method utilizes specific angular increments by dividing the angle by a golden ratio factor. Uniformly distributed points are generated on the sphere by calculating the polar and azimuthal angles. To solve the problem, the Cartesian coordinate system needs to be converted into a polar coordinate system. The polar angle is calculated using the inverse cosine sampling method:(11)

Fig. 3. Schematic diagram of uniformly distributed points generated on the sphere.
The calculation formula for the azimuth angle is(12)where n is the number of points on the sphere, set the spherical center coordinate as Oc (xc, yc, zc), and r as the radius of the obstacle sphere. Then the coordinate Pi (xi, yi, zi) of the i-th point generating a uniform distribution on the sphere is given by:(13)
Icosahedron Subdisivion (IS) and Simulated Annealing (SA) [38] are utilized to generate uniformly distributed points on a spherical surface, and the running times of the three algorithms are compared. The data in Fig. 4 shows that FS has a clear advantage, running faster than other methods in the obstacle modeling process.

Fig. 4. Comparison of the generation time of obstacle points by the SA, IS, and FS methods.
To achieve a more accurate equivalence between the generated points and the original sphere, it is essential to analyze the distribution uniformity of the generated points. For the IS method, the number of uniformly distributed points on the surface of the sphere is limited, and the quantity of generated points can only be indirectly controlled by adjusting the number of subdivisions. Therefore, when comparing the uniformity error, the main focus is on analyzing the SA and FS methods. In the scenario where different numbers of points are generated by the two methods, a random center point is selected. The distances between the points in the cap area and the center point are then calculated. The mean value, variance, standard deviation, and absolute deviation from the median of the distances are used as evaluation criteria to assess the uniformity error.
As depicted in Fig. 5, when the same uniformly distributed obstacle points are generated by the two different methods on the sphere, the distances between the points generated by the FS method exhibit smaller changes and a reduced dispersion degree compared to those generated by the SA method. Additionally, the absolute deviation of the center point is smaller for the FS, indicating that the FS method demonstrates better stability, accuracy, and robustness in generating the same number of uniformly distributed spherical points than the SA method. Fig. 6 illustrates the surfaces of spheres with uniformly distributed obstacle points generated by the FS method, along with a magnified view of a randomly selected cap area of the spheres.

Fig. 5. Comparison of different parameters for evaluating the uniformity of generated points by the SA and FS methods.

Fig. 6. Schematic of spherical uniformly distributed obstacle points and partially enlarged region.
3.2. Refined obstacle boundary model using B-spline curves
In three-dimensional obstacle avoidance path planning, smooth paths can be easily generated using B-spline curves, which improves the feasibility and maneuvering safety of obstacle avoidance paths [39,40]. Moreover, B-spline curves play a crucial role in path planning for robots, aircraft, and autonomous vehicles, finding significant applications in these domains [41]. After employing the FS method to model the obstacles and obtaining the homogeneous equivalent obstacle points, the local repulsion potential field boundary model is established by utilizing B-spline curves. When the aircraft enters the influence range of the repulsion potential field, an obstacle avoidance profile is generated by setting control points near the obstacle points.
In the three-dimensional coordinate system, the boundary conditions are as follows: starting point Ps (xs, ys, zs), target point Pm (xm, ym, zm), starting point velocity v0 (0,0,0), end velocity vm (0,0,0), maximum flight velocity vmax=14 m/s, and acceleration 1 m/s2≤ ai ≤5 m/s2. When the aircraft is affected by obstacles, the resultant force potential field function is:(14)
The aircraft experiences a resultant force of:(15)
In each iteration, it is essential to ensure that the acceleration and velocity constraints are met. If the step length of a single iteration is less than l0 or the Angle is less than α0, m changes from 0 to 1, and the repulsion potential field is strengthened. When the aircraft, the obstacle, and the target point are aligned, the flight speed is directly updated to:(16)
The APF method is employed to generate the path in the initial stage. When the distance between the aircraft and the obstacle becomes less than the safety threshold, the current position of the aircraft is considered the starting point for the obstacle region. Assuming that the starting point of the obstacle area is denoted as Pobs0 (xobs0, yobs0, zobs0), and the target point is represented by Pm=(xm, ym, zm), the parametric equation of the line L0, which passes through the starting point and the target point of the obstacle area, is as follows:(17)
In this equation, (x, y, z) denotes any point on the line L0, and t is the parameter that varies along the line, determining the position of points between Pobs0 and Pm. By adjusting the value of t, different points along the line L0 can be obtained. Establish the plane A where L0 is located, and make the normal vector n = (a, b, c) parallel to the Y-Z plane. Then, the point normal of plane A is:(18)
As a vertical line is drawn from the center of the obstacle sphere to plane A, the distance is denoted as d. The point where the vertical line intersects the plane is considered the center, denoted as O1, of the circle formed by the intersection between the plane and the sphere. The radius of this intersection circle is:(19)
The expression for the intersecting circles is the combination of plane and sphere equations:(20)
The command [a(∆x) + b(∆y) + c(∆z)] = ε, where (∆x), (∆y), and (∆z) represent the differences in the x, y, and z coordinates between the starting point Pobs0 (xobs0, yobs0, zobs0) and the center of the obstacle sphere Oc. The x, y and z coordinates of the intersecting circles satisfy the formula:(21)(22)(23)
The obstacle points that the aircraft needs to avoid are located on the partial arc of the circle. Assuming that plane A intersects the spherical obstacle and forms an intersecting circle surface denoted as S1, the center of this intersecting circle O1 is connected to both Pobs0 and Pm, forming an included angle ω. The arc lobs corresponding to the angle ω is the arc that needs to be avoided. If there are μ obstacle points on this arc, a safe distance Lsa is set as the distance between the path points and Oc. The direction from O1 to each obstacle point is taken as the control direction, and u+1 control points Pj (j=0, 1,2, …, μ) are set along this direction with a length of Lsa-r1.
Suitable u+1 knot vectors T = [t1, t2, ..., tu+1] are chosen, and the k-th order B-spline curve is used [42]:(24)where Bj,k(t) represents the polynomial coefficient of the control point coordinate influence weight, specifically indicating the value of the j-k-order B-spline basis function at the parameter t. Pj represents the j-th control point. The number of control points, knot vectors, and order satisfy the relationship of m=μ+k+1, where m is the total number of control points. The choice of order and control points significantly affects the shape and behavior of the B-spline curve. The specific B-spline obstacle avoidance strategy is shown in Fig. 7.

Fig. 7. Strategy of generating obstacle boundary curve with B-spline.
To ensure the smoothness of the path in addition to the obstacle avoidance task from the starting point to the target point, the formula for calculating the smoothness of the X-Y path is as follows:(25)where i represents the i-th path point, and Kxy denotes the path curvature in the X-Y coordinate system of the three-dimensional path. The curvature Kxy is used to measure the smoothness of the path while a smaller value of Kxy indicates a smoother path. When the line connecting Pobs0 and Pm is exactly the diameter of intersecting circular surface, it implies that the projection of the line between the center of the sphere and Pobs0 onto the intersecting circular surface is equal to the radius of the circle. Consequently, the obstacle avoidance arc takes the form of a semicircle. In this situation, the obstacle boundary curve is established by selecting half of the circular arc, which contains a higher concentration of obstacle points.
3.3. Obstacle avoidance path planning method
The aircraft's entire flight path planning is divided into two distinct stages. In the first stage, the initial path is generated using the APF method based on the starting and ending information. As the aircraft approaches an obstacle while following the prescribed path, it enters the second stage to perform obstacle avoidance. The starting point of the obstacle area is determined by identifying the first point on the initial path where the distance from the obstacle point is less than the safety threshold. The selection of the effective obstacle arc is based on the position information of the starting point within the obstacle area and the global target point. By establishing suitable control points and node vectors, B-spline curves are employed to fit the obstacle boundary, facilitating obstacle avoidance. The steps involved in the local obstacle avoidance and path optimization algorithm are as follows:
Step 1: The spherical obstacle model is constructed by specifying the position of the center of the obstacle and defining the threat radius. The FS method is employed to uniformly distribute obstacle points on the surface of a sphere, thereby creating an equivalent obstacle sphere.
Step 2: Based on the position information of the starting point and the endpoint, the initial three-dimensional path is generated using the adaptive step size strategy and an IAPF method.
Step 3: According to the established obstacle model, the initially planned waypoints are continuously assessed in real-time to determine whether they are within potential collision zones of obstacles.
Case 4: The distance between the path point and the obstacle ball is less than the safety threshold, the path from the hazardous area to the target point is re-planned using the obstacle avoidance strategy based on B-splines.
Case 5: The initially planned path points are located outside the potentially colliding region, the aircraft can safely follow the initial path without any risk of collision, reaching the target point successfully.
To illustrate the procedure of the BF-IAPF algorithm more clearly, the pseudocode has been presented in Table 1.
4. Simulation results and analysis
In this section, the effectiveness of the proposed obstacle avoidance strategy and the F-IAPF algorithm was validated by planning a collision-free path in a simulated three-dimensional flight environment with various obstacles. The simulation is executed on a computer with the Intel(R) Core(TM) i5–8265 U CPU @ 1.60 GHz, 8GB RAM and windows 11 64-bit operating system, and the simulation platform is MATLAB R2021b.
To comprehensively evaluate the BF-IAPF method, we consider three key aspects in our simulation experiments: addressing local minima, pathfinding success rate, and path smoothness. First, we validate its effectiveness in handling local minima. Second, we conduct a comparative analysis, assessing its success rate and contribution to path smoothness in comparison to other algorithms. Lastly, we validate its performance in complex environments.
4.1. The simulation of local minimum problems
One of the most common issues encountered in traditional artificial potential field methods is the occurrence of "deadlock" when the aircraft becomes collinear with the obstacle and the target point during flight path planning.
The traditional artificial potential field method:
To validate the issue of path points encountering local minima, simulation experiments were conducted in multiple scenarios where the drone, obstacles, and target point were collinear. The coordinates of the starting point and destination were set at (0, 0, 0) and (10, 10, 10), respectively. The parameters for the obstacles are provided in Table 2. Fig. 8(a) shows the scenario where the path points get trapped in local minima, preventing the vehicle from reaching the target point. In addition, even if there is no collinear situation among the start, obstacles, and target, there will still be failure of path planning with the TAPF in the environment with the parameters listed in Tables 2 and 3. When multiple obstacle spheres differ in size, it is challenging to define a singular precise value of the repulsion range. This uncertainty could potentially lead to the path points near the obstacle are not sufficiently corrected which leads to the planned path intersecting with obstacles, as shown in Fig. 8(b).
Table 2. Parameters of obstacles with the issue of local minima.
| Empty Cell | Coordinates of the center | Radius | Repulsive field range |
|---|---|---|---|
| Obs1 | (4,4,4) | 0.5 | 2 |
| Obs2 | (3,8,5) | 0.5 | 2 |
| Obs3 | (5,7,6) | 1 | 2 |
| Obs4 | (5,4,7) | 1 | 2 |
| Obs5 | (8,2,6) | 1 | 2 |
| Obs6 | (8,8,9) | 1.2 | 2 |

Fig. 8. Simulation of different scenarios with traditional artificial potential field method.
Table 3. The obstacle parameters of the paths crossing.
| Empty Cell | Coordinates of the center | Radius | Repulsive field range |
|---|---|---|---|
| Obs1 | (3,1,2) | 1.5 | 2 |
| Obs2 | (3,8,5) | 1 | 2 |
| Obs3 | (6,7,6) | 1 | 2 |
| Obs4 | (8,2,6) | 1 | 2 |
| Obs5 | (8,8,8) | 1 | 2 |
The APF algorithm combined with the Fibonacci Sphere:
The obstacle model of the Fibonacci Sphere method proposed in Section 3.1 is employed to generate uniformly distributed equivalent points serving as the repulsive force source on the surface of the sphere. Keeping the two environmental parameters consistent with those in Section 4.1, simulation experiments were performed using the F-IAPF method. The simulation results of overcoming the local minima and crossing obstacles are shown in Fig. 9, respectively. It is evident that the F-IAPF method could effectively make the waypoints escape local optimum. Furthermore, as the points on the surface of the obstacle sphere directly serve as sources of repulsion, it allows a more precise and consistent repulsive field range for the generated paths that successfully reaches the target point without collision. This issue is verified in Fig. 9(b).

Fig. 9. Paths generated by the F-IAPF.
Additionally, after conducting an extensive series of simulation experiments, we have discovered that combining the Fibonacci Sphere with TAPF separately can to some extent effectively prevent path points from falling into local minima. In scenarios with 1to 20 randomly distributed obstacles, the paths were generated using the TAPF, F-TAPF, and F-IAPF algorithm. Distance calculations for the endpoints of each path to the target points are summarized in Table 4, and the evolution of the distance between path points and target points during the iteration process is depicted in Fig. 10(a). From Table 4, it can be indicated that the F-TAPF and F-IAPF methods can successfully avoid the local minima and lead the endpoint of the generated path to the desired destination area with satisfactory precision. We expanded the experiment scenarios by altering the target point and calculated the distances between the endpoint of each path and the expected target point, as shown in Fig. 10(b). The path points generated using F-TAPF method get trapped in local minima, probably because the repulsive forces exerted by the multiple obstacle points happen to be equal in magnitude but opposite in direction to the attractive forces. However, F-IAPF method can regulate waypoints near local minima to gradually tend to escape from the oscillating region by introducing a velocity potential field regulation mechanism. Eventually, it bypasses the obstacles and reaches the target region with a 100 % success rate.
Table 4. Statistical results in collinear cases.
| Number of obstacles | Distance between end point and target | ||
|---|---|---|---|
| Empty Cell | TAPF | F-TAPF | F-IAPF |
| 1 | 11.05624 | 0.22021 | 0.17335 |
| 2 | 8.15867 | 0.1903 | 0.16721 |
| 3 | 12.75624 | 0.2782 | 0.21056 |
| 4 | 0.27626 | 0.20247 | 0.16577 |
| 5 | 5.92497 | 0.19389 | 0.11758 |
| 6 | 11.0461 | 11.75387 | 0.20305 |
| 7 | 0.24621 | 0.2072 | 0.23235 |
| 8 | 5.94974 | 0.2364 | 0.18543 |
| 9 | 10.03516 | 14.26572 | 0.13002 |
| 10 | 7.49549 | 0.13321 | 0.12541 |
| 11 | 4.33367 | 0.12474 | 0.18292 |
| 12 | 11.07031 | 11.14173 | 0.12433 |
| 13 | 0.25571 | 0.15415 | 0.18818 |
| 14 | 12.74513 | 8.22771 | 0.27728 |
| 15 | 12.02206 | 0.17504 | 0.17426 |
| 16 | 0.23484 | 0.16548 | 0.13907 |
| 17 | 11.0246 | 0.27086 | 0.17335 |
| 18 | 12.79639 | 0.23407 | 0.16721 |
| 19 | 0.26432 | 0.21919 | 0.21056 |
| 20 | 9.33625 | 0.24904 | 0.16577 |

Fig. 10. Distance between waypoints and the target point in the different 'deadlock' scenarios (methods TAPF, F-TAPF, and F-IAPF).
4.2. Comparision and analysis of path smoothness
In the context of path planning and navigation, rapid changes in trajectory place higher loads on the UAV. This can hinder its ability to respond quickly and may lead to spatial or temporal instability during flight.
In this section, we have compared the smoothness of the paths generated by the F-TAPF and artificial potential field optimized by point of tangency (PT-APF) [43] with the proposed approach. The PT-APF method still encounters situations where path points are trapped in local minima when obstacles, starting points, and targets are co-linear. Therefore, we conducted a simulation experiment to compare the smoothness of paths generated by the three methods. We set the starting point and target point to (0, 0, 0) and (10, 10, 10), respectively, with the obstacle's center coordinate at (6.1, 6, 6). The simulation results are shown in the following Fig. 11. Fig. 11(a), (b) and (c) show the generated path in three-dimensional environment while their corresponding curvature curves in the X-Y, X-Z, and Y-Z coordinate systems are illustrated in Fig. 11(d), (e), and (f), respectively. The maximum and average curvature values of the paths generated by the three methods, when projected onto a two-dimensional coordinate system, are listed in Table 5. According to the results in Table 5, the path smoothness of the proposed method is significantly higher than the other two algorithms with the smoothness improvement of 69 % and 98 %, respectively.

Fig. 11. Path planning results of F-IAPF, BF-IAPF, and PT-APF in a single spherical obstacle environment.
Table 5. Curvature values of paths generated by the BF-IAPF, PT-APF, and F-IAPF methods.
| Curvature value | BF-IAPF method | PT-APF method | F-IAPF method | |||
|---|---|---|---|---|---|---|
| Empty Cell | Max | Mean | Max | Mean | Max | Mean |
| X-Y | 0.0183 | 0.0016 | 0.2228 | 0.0079 | 2.6084 | 0.0219 |
| X-Z | 0.0183 | 0.0016 | 0.2228 | 0.0079 | 0.955 | 0.0078 |
| Y-Z | 0.0183 | 0.0017 | 0.4141 | 0.0091 | 0.3496 | 0.0054 |
| The improved smoothness of BF-IAPF method | 69 % | 98 % | ||||
4.3. Simulation in complex environments
To assess the effectiveness of the proposed algorithm for path planning in different scenarios, we have introduced six scenarios with varying number and location of obstacles. The generated path in each scenario could successfully reach the target by avoiding the local minima, as shown in Fig. 12. Building upon this foundation, we enhanced the environmental complexity and randomness by adjusting both obstacle and target point coordinates. Subsequently, we conducted a series of 40 simulation experiments and generated distance variation plots illustrating the evolving distances between each path point and the target point during the iterative process. As depicted in Fig. 13, it is evident that the distances between the waypoints of the 40 paths and the target point ultimately achieved complete convergence. The curve illustrating the changes in distance exhibited a notably smooth and continuous trend.

Fig. 12. Simulation results in different scenarios with multi-obstacles using the proposed method.

Fig. 13. Distance variation of each path points to the target point during iteration.
Fig. 14(a) illustrates the variations in the velocity potential field during the obstacle avoidance path generation process with the attraction coefficient katt = 20 and the repulsion factor η = 80. Higher values indicate that the vehicle is more inclined to move towards that position, while lower value areas are near obstacles and represent the vehicle's avoidance zones. When complex environmental constraints and objective functions are present, this kind of discontinuous velocity fields can adapt more flexibly to the evolving flight environment than the continuous velocity fields [44,45]. This is due to the fact that the velocity field can dynamically adjust its required speed to avoid obstacles based on the diversity of the environment. The evolution of total potential energy during the iteration process is shown in Fig. 14(b). It can be observed from the graph that, with an increase in the number of iterations, the total potential energy at the vehicle's position continuously decreases. This indicates that the vehicle steadily approaches the target point, culminating in the termination of the iteration process upon reaching the target area.

Fig. 14. Distribution of the velocity field and total potential energy in each of the 40 scenarios with different numbers of obstacles.
5. Conclusion
The application of the APF in the field of path planning has become highly prevalent in generating a collision-free route from the starting point to the destination. However, the traditional APF algorithm has the shortcoming of local minimum. The detection mechanism of local minimum was introduced into the APF algorithm to address this issue. To quantitatively quantify information about three-dimensional obstacle spheres, the obstacle model was built by the Fibonacci Sphere method realizing the elevation of obstacle constraints from two-dimensional to three-dimensional. In addition, the path curvature was reduced by the proposed obstacle boundary using the B-spline curve. Accurate obstacle avoidance of a aircraft on the surface of an obstacle sphere is achieved by static obstacle environment simulation. The algorithm effectively mitigates the local minimum problem and ensures smooth connections and transitions on the flight path. The path planned by the proposed algorithm exhibited a smoothness improvement of 68 % and 98 %, respectively compared to the PT-APF and F-IAPF method. This approach is well-suited for obstacle avoidance path planning in both single and multiple static obstacle environments.
The proposed algorithm elevates the conventional two-dimensional path planning problem to a three-dimensional complex flight environment. It transitions from the traditional approach to 2D obstacles to a more sophisticated approach to obstacle avoidance using equivalent particles on a sphere that enhances the obstacle avoidance capability. This improvement solves the problem of excessive or insufficient turn angles for obstacle avoidance, producing a more accurate and efficient collision-free path. Future work will concentrate on the following areas:
- 1)
Considering the physical characteristics of unmanned aerial vehicles (UAVs), dynamic models and incorporate additional constraints will be established, such as maneuverability and heading constraints. These constraints will be integrated with control algorithms to achieve a more advanced path planning.
- 2)
Building upon the obstacle model introduced in this paper, various obstacle models will be investigated to better capture the physical characteristics of real-world obstacles and enhance their applicability.
- 3)
The positions and velocities of spatial obstacles will be considered to improve obstacle avoidance strategy. The path planning algorithm incorporate with the dynamic characteristics of spatial obstacles could better respond to real-time environmental changes.
Declaration of Competing Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Acknowledgments
The project was supported by the National Natural Science Foundation of China (No. 52075278).
Data availability
Data will be made available on request.
References
- [1]
F. Nex, C. Armenakis, M. Cramer, D.A. Cucci, M. Gerke, E. Honkavaara, A. Kukko, C. Persello, J. Skaloud
UAV in the advent of the twenties: where we stand and what is next
ISPRS J. Photogramm. Remote Sens., 184 (2022), pp. 215-242
- [2]
Quadratic programming-based approach for autonomous vehicle path planning in space
Chin. J. Mech. Eng., 25 (2012), pp. 665-673
- [3]
O. Khatib
Real-time obstacle avoidance for manipulators and mobile robots
Proceedings. 1985 IEEE International Conference on Robotics and Automation, Institute of Electrical and Electronics Engineers, St. Louis, MO, USA (1985), pp. 500-505
- [4]
W.E. Howden
The sofa problem
Comput. J., 11 (1968), pp. 299-301
- [5]
C. Li, X. Huang, J. Ding, K. Song, S. Lu
Global path planning based on a bidirectional alternating search A* algorithm for mobile robots
Comput. Ind. Eng., 168 (2022), Article 108123
- [6]
J. Guo, W. Xia, X. Hu, H. Ma
Feedback RRT* algorithm for UAV path planning in a hostile environment
Comput. Ind. Eng., 174 (2022), Article 108771
- [7]
W. Wang, H. Deng, X. Wu
Path planning of loaded pin-jointed bar mechanisms using rapidly-exploring random tree method
Comput. Struct., 209 (2018), pp. 65-73
- [8]
C. Miao, G. Chen, C. Yan, Y. Wu
Path planning optimization of indoor mobile robot based on adaptive ant colony algorithm
Comput. Ind. Eng., 156 (2021), Article 107230
- [9]
A. Bakdi, A. Hentout, H. Boutami, A. Maoudj, O. Hachour, B. Bouzouia
Optimal path planning and execution for mobile robots using genetic algorithm and adaptive fuzzy-logic control
Rob. Auton. Syst., 89 (2017), pp. 95-109
- [10]
M. Rampavan, E.P. Ijjina
Genetic brake-net: deep learning based brake light detection for collision avoidance using genetic algorithm
Know. Based Syst., 264 (2023)
- [36]
V. Sezer, M. Gokasan
A novel obstacle avoidance algorithm: “follow the gap method”
Rob. Auton. Syst., 60 (2012), pp. 1123-1134
- [37]
Á. González
Measurement of areas on a sphere using fibonacci and latitude–longitude lattices
Math. Geosci., 42 (2010), pp. 49-64
- [38]
S. Kirkpatrick, C.D. Gelatt, M.P. Vecchi
Optimization by simulated annealing
Science, 220 (1983), pp. 671-680
- [39]
X. Li, X. Gao, W. Zhang, L. Hao
Smooth and collision-free trajectory generation in cluttered environments using cubic B-spline form
Mech. Mach. Theory, 169 (2022), Article 104606
- [40]
N. Wang, Y. Zhang, C.K. Ahn, Q. Xu
Autonomous pilot of unmanned surface vehicles: bridging path planning and tracking
IEEE Trans. Veh. Technol., 71 (2022), pp. 2358-2374
- [41]
Q. Hu, J. Xie, C. Wang
Dynamic path planning and trajectory tracking using MPC for satellite with collision avoidance
ISA Trans., 84 (2019), pp. 128-141
- [42]
H. Xu, Q. Hu
Approximating uniform rational B-spline curves by polynomial B-spline curves
J. Comput. Appl. Math., 244 (2013), pp. 10-18
- [43]
Y. Peng, W. Guo, M. Liu, J. Cui, S. Xie
Obstacle avoidance planning based on artificial potential field optimized by point of tangency in three-dimensional space
J. Syst. Simul., 26 (2014), pp. 1758-1762
- [44]
S.P. Bhat, D.S. Bernstein
A topological obstruction to continuous global stabilization of rotational motion and the unwinding phenomenon
Syst. Control Lett., 39 (2000), pp. 63-70
- [45]
T. Kunimune, Y. Fukui, T. Wada
Passive velocity field control with discontinuous desired velocity fields: non-smooth potential gradient vector field by locally semiconcave functions
2016 IEEE International Conference on Robotics And Biomimetics (ROBIO), IEEE, New York (2016), pp. 1165-1172
Cited by (0)
© 2023 Elsevier Masson SAS. All rights reserved.
Z. Wu, J. Dai, B. Jiang, H.R. Karimi
Robot path planning based on artificial potential field with deterministic annealing
S.S. Ge, Y.J. Cui
Dynamic motion planning for mobile robots using potential field method
Auton. Robots, 13 (2002), pp. 207-222
D. González, J. Pérez, V. Milanés, F. Nashashibi
A Review of Motion Planning Techniques for Automated Vehicles
IEEE Trans. Intell. Transp. Syst., 17 (2016), pp. 1135-1145
Z. Pan, C. Zhang, Y. Xia, H. Xiong, X. Shao
An improved artificial potential field method for path planning and formation control of the multi-UAV systems
IEEE Trans. Circuits Syst. Express Briefs, 69 (2022), pp. 1129-1133
Y. Koren, J. Borenstein
Potential field methods and their inherent limitations for mobile robot navigation
1991 IEEE International Conference on Robotics and Automation Proceedings (1991), pp. 1398-1404
C. Wang, Z. Wang, L. Zhang, H. Yu, D. Cao
Post-impact motion planning and tracking control for autonomous vehicles
Y. Shin, E. Kim
Hybrid path planning using positioning risk and artificial potential fields
Aerosp. Sci. Technol., 112 (2021), Article 106640
L. Hao, D. Liu, S. Du, Y. Wang, B. Wu, Q. Wang, N. Zhang
An improved path planning algorithm based on artificial potential field and primal-dual neural network for surgical robot
Comput. Methods Programs Biomed., 227 (2022), Article 107202
G. Fedele, L. D'Alfonso, F. Chiaravalloti, G. D'Aquila
Obstacles avoidance based on switching potential functions
J. Intell. Robotic Syst., 90 (2018)
H. Rezaee, F. Abdollahi
A decentralized cooperative control scheme with obstacle avoidance for a team of mobile robots
IEEE Trans. Ind. Electron., 61 (2014), pp. 347-354
Z. Li, X. Yang, X. Sun, G. Liu, C. Hu
Improved artificial potential field based lateral entry guidance for waypoints passage and no-fly zones avoidance
Aerosp. Sci. Technol., 86 (2019), pp. 119-131
J. Fan, X. Chen, X. Liang
UAV trajectory planning based on bi-directional APF-RRT* algorithm with goal-biased
Expert Syst. Appl., 213 (2023)
S. Hassan, J. Yoon
Haptic assisted aircraft optimal assembly path planning scheme based on swarming and artificial potential field approach
Adv. Eng. Software, 69 (2014), pp. 18-25
O. Montiel, U. Orozco-Rosas, R. Sepúlveda Cruz
Path planning for mobile robots using bacterial potential field for avoiding static and dynamic obstacles
Expert Syst. Appl., 42 (2015), pp. 5177-5191
F. Sui, X. Tang, Z. Dong, X. Gan, P. Luo, J. Sun
ACO+PSO+A*: a bi-layer hybrid algorithm for multi-task path planning of an AUV
Comput. Ind. Eng., 175 (2023), Article 108905
W. Zhang, Y. Zeng, S. Wang, T. Wang, H. Li, K. Fei, X. Qiu, R. Jiang, J. Li
Research on the local path planning of an orchard mowing robot based on an elliptic repulsion scope boundary constraint potential field method
Front. Plant Sci., 14 (2023)
J. Rao, C. Xiang, J. Xi, J. Chen, J. Lei, W. Giernacki, M. Liu
Path planning for dual UAVs cooperative suspension transport based on artificial potential field-A* algorithm
Knowl Based Syst., 277 (2023), Article 110797
A.M.H. Aljassani, S.N. Ghani, A.M.H. Al-Hajjar
Enhanced multi-agent systems formation and obstacle avoidance (EMAFOA) control algorithm
Results Eng., 18 (2023), Article 101151
J. Hwang, J. Lee, C. Park
Collision avoidance control for formation flying of multiple spacecraft using artificial potential field
Adv. Space Res., 69 (2022), pp. 2197-2209
X. Chai, Z. Zheng, J. Xiao, L. Yan, B. Qu, P. Wen, H. Wang, Y. Zhou, H. Sun
Multi-strategy fusion differential evolution algorithm for UAV path planning in complex environment
Aerosp. Sci. Technol., 121 (2022), Article 107287
D. Zheng, X. Wu, Y. Liu, J. Pang
A dynamical system approach to real-time three-dimensional concave obstacle avoidance
2020 IEEE/ASME International Conference on Advanced Intelligent Mechatronics (AIM), IEEE, Boston, MA, USA (2020), pp. 1082-1087
Y. Xiuxia, Z. Yi, Z. Weiwei
Obstacle avoidance method of three-dimensional obstacle spherical cap
J. Syst. Eng. Electron., 29 (2018), pp. 1058-1068
A. Chakravarthy, D. Ghose
Obstacle avoidance in a dynamic environment: a collision cone approach
Trans. Sys. Man Cyber. Part A, 28 (1998), pp. 562-574
C.Y. Tan, S. Huang, K.K. Tan, R.S.H. Teo, W.Q. Liu, F. Lin
Collision avoidance design on unmanned aerial vehicle in 3D space
Un. Sys., 06 (2018), pp. 277-295
Y. Jenie, E.J. Van Kampen, C. De Visser, J. Ellerbroek, J. Hoekstra
Three-dimensional velocity obstacle method for uncoordinated avoidance maneuvers of unmanned aerial vehicles
J. Guidance Control Dyn., 39 (2016), pp. 1-12
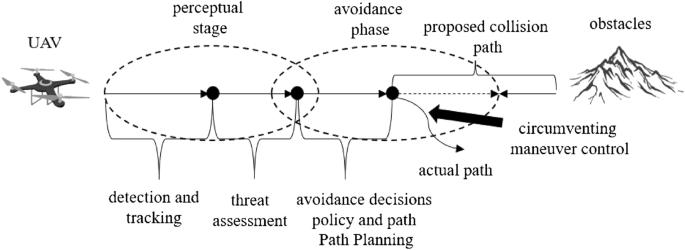
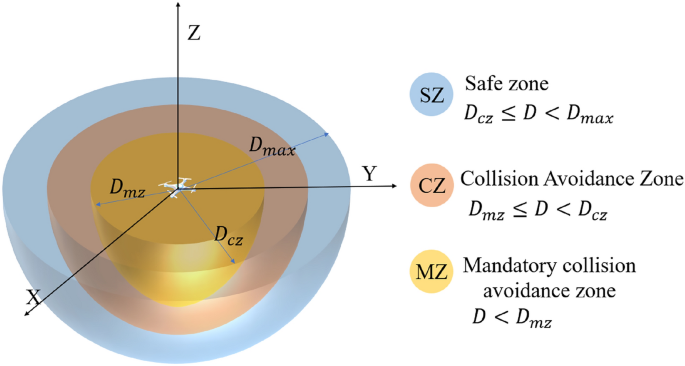
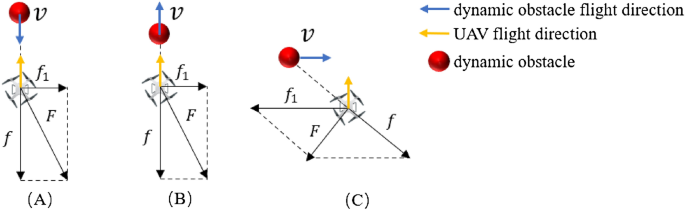
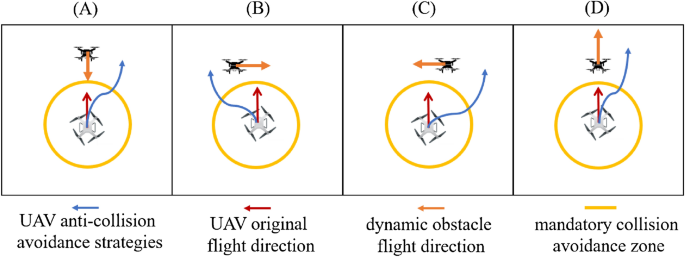
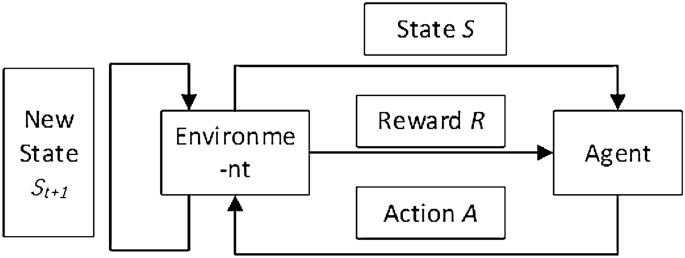
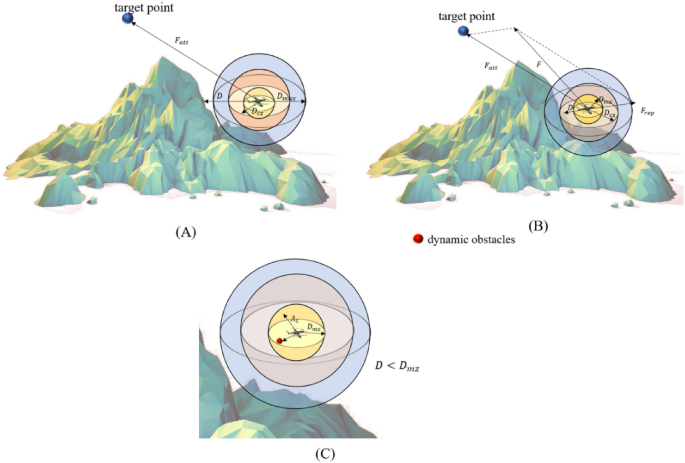

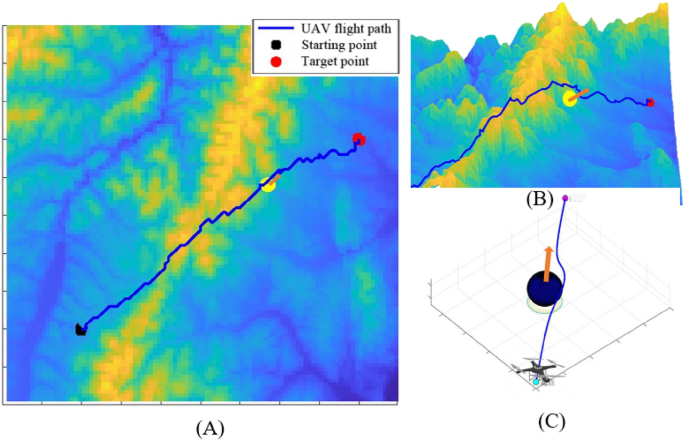
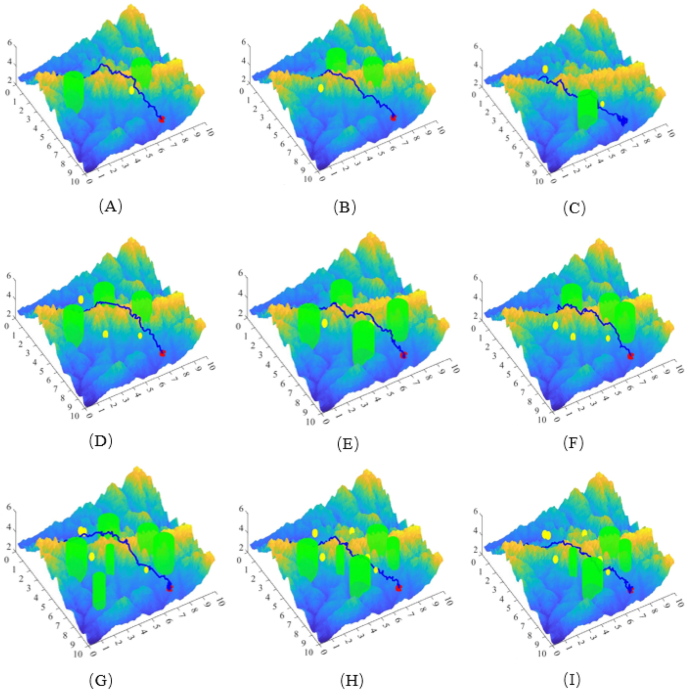
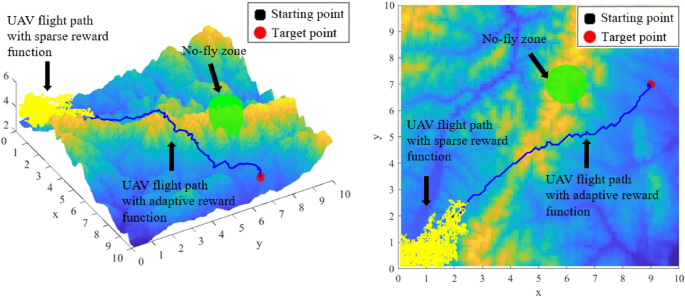
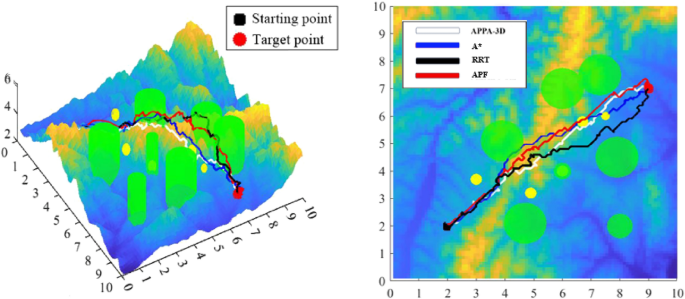
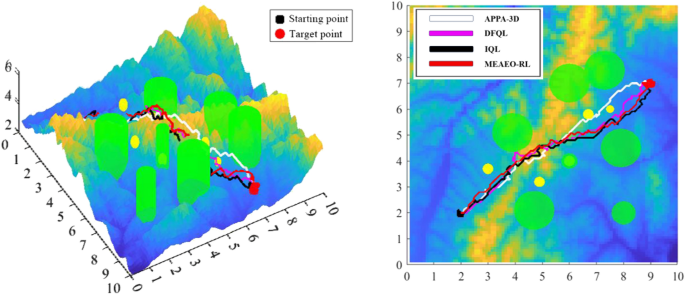
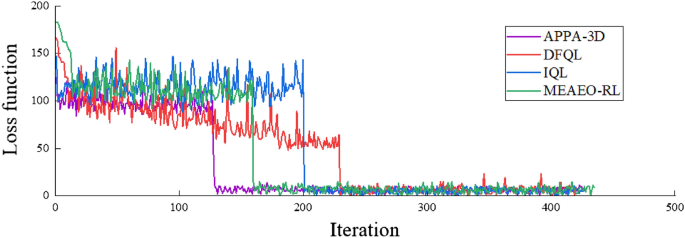




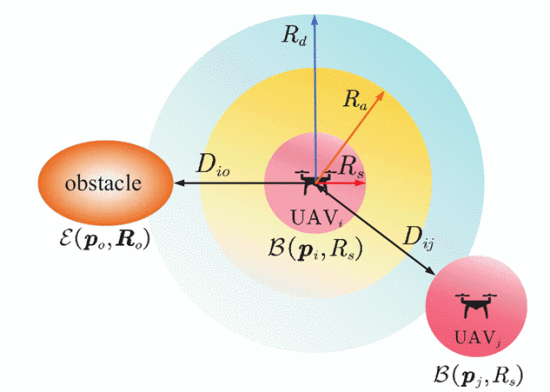

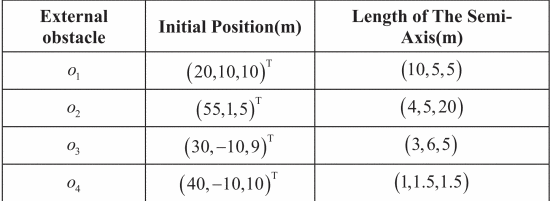
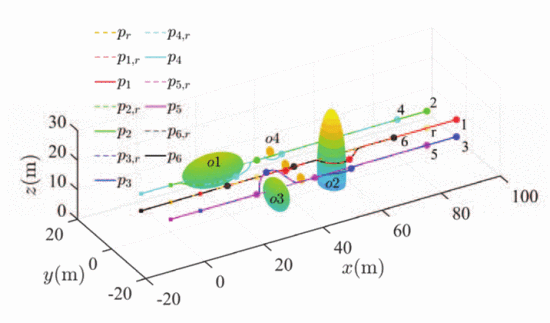





No comments:
Post a Comment