Hyperbolic frequency-modulated bat calls using hyperbolic scale transform and PHS HFM Sonar

The estimated IFs obtained by FRFT. (a) Eighth bat call. (b) Ninth bat call.

Summary of HFM Advantages and Disadvantages

Here are some key advantages and disadvantages of using hyperbolic frequency modulation (HFM) signals for sonar:

Advantages:

1. Doppler invariance - HFM signals have inherent Doppler invariant characteristics, making them well-suited for detecting moving targets.
2. Tolerant to moving targets - HFM can still produce peaks after matched filtering even at high target speeds, unlike linear FM signals.
3. Can use different frequency bands - HFM signals of different frequency bands can be combined in a pulse sequence, helping overcome propagation loss issues in certain frequency bands.
4. Improved accuracy - Using multiple HFM signals allows for mutual calculation of speed and distance, reducing errors compared to single signal calculations.
5. Suitable for coherent integration - The phase information can be preserved for coherent integration across pulse sequences, improving signal-to-noise ratio.

Disadvantages:

1. Complex processing - Requires more complex signal processing compared to simpler waveforms like continuous wave signals.
2. Coupling of velocity and distance - The ambiguity function of HFM has a "blade" shape, coupling velocity and distance measurements.
3. Time delay issues - Doppler shifts cause time delays after matched filtering, making ranging difficult with a single HFM pulse.
4. Frequency band limitations - A single HFM signal may have too much transmission loss in certain frequency bands of the underwater channel.
5. SNR requirements - Low SNR can still lead to errors in arrival time estimation and peak detection.
6. Computational complexity - Processing multiple HFM signals in a sequence increases the computational requirements.

In summary, while HFM offers significant advantages for sonar, especially for moving target detection, it also comes with increased complexity in signal design and processing. The use of HFM pulse sequences helps mitigate some single-pulse limitations but requires more sophisticated systems. 

Bat Sonar

Bats use hyperbolic frequency modulated (HFM) sonar in several sophisticated ways:

1. Echolocation: Bats emit HFM calls and use the echoes to navigate and locate prey. The document mentions that echolocating bats have acquired capabilities through evolution that are more intelligent and efficient than existing synthetic systems.

2. Waveform variation: Bats vary their waveforms during different phases of prey pursuit - searching, approaching, and capturing. This allows them to optimize their sonar for each stage of hunting.

3. Multiple harmonics: Bat calls often contain multiple harmonics with large energy differences. This may help them gather more information about their environment and targets.

4. Doppler compensation: Some bats, like the hipposiderid bat, can precisely compensate for Doppler shifts in their calls. This helps them accurately detect moving prey.

5. Clutter suppression: Bats use echo harmonic structure to distinguish their targets from background clutter.

6. Target recognition: The document suggests bats may use trends in call parameters for species identification of prey.

7. Ranging accuracy: Bats appear to adjust their call parameters (like decreasing intra-pulse delay) to improve ranging accuracy as they approach prey.

8. Adaptive beam steering: Some bats, like Egyptian fruit bats, can control their sonar beam direction by adjusting their tongues, similar to phased array radar.

9. Wideband signals: Bat calls are often wideband FM signals, which can provide more information about targets than narrowband signals.

10. Optimal Doppler tolerance: The HFM waveforms used by bats are thought to be optimized for Doppler tolerance, allowing them to detect prey moving at various speeds.

The document emphasizes that bat sonar capabilities have evolved over millions of years and are in many ways superior to human-made sonar systems. Researchers are studying bat sonar to improve biomimetic technologies and synthetic echolocation systems. 

PHS Sonar

PHS (Pulse sequence method based on Hyperbolic Frequency Modulation) sonar is an approach described in the document that aims to improve speed measurement and ranging accuracy using multiple HFM signals. Here's a breakdown of how it works and how it compares to bat sonar:

How PHS uses HFM:

1. Multiple HFM signals: PHS uses a sequence of HFM signals with different frequency bands and pulse widths.

2. Velocity measurement: It calculates target velocity by comparing the time delays between different HFM signals after matched filtering.

3. Ranging: PHS uses the relationships between multiple HFM echoes to improve ranging accuracy.

4. Coherent integration: It allows for coherent integration across pulse sequences to improve signal-to-noise ratio.

5. Adaptability: By using multiple frequency bands, PHS can overcome issues with excessive propagation loss in certain frequency ranges.

Comparison to bat sonar:

Similarities:
1. Use of HFM: Both PHS and bat sonar utilize HFM signals for their Doppler invariant properties.
2. Multiple frequency bands: Bats use multiple harmonics, while PHS uses different frequency bands across pulses.
3. Adaptability: Both systems can adapt to different environmental conditions and target scenarios.

Differences:
1. Complexity: Bat sonar is likely more sophisticated, having evolved over millions of years.
2. Real-time processing: Bats process sonar information in real-time with highly evolved neural systems, while PHS relies on digital signal processing.
3. Emission control: Bats can dynamically control their call emissions, including beam steering, which isn't mentioned as a feature of PHS.
4. Bandwidth: Bat calls often cover a wider frequency range than typical PHS implementations.
5. Integration with other senses: Bats integrate sonar with other sensory inputs, which PHS doesn't do.

Advantages of PHS over single HFM:
1. Improved accuracy: PHS can achieve better ranging and speed measurement accuracy than single HFM signals.
2. Resilience to channel effects: Using multiple frequency bands helps overcome issues with propagation loss in specific frequencies.
3. Flexibility: PHS can be adjusted for different scenarios by changing the HFM signal parameters in the sequence.

While PHS represents an advancement in synthetic sonar systems using HFM, it still doesn't match the full capabilities and adaptability of bat sonar. However, it demonstrates how principles observed in bat echolocation can be applied to improve human-made sonar systems.

Parameter estimation of the hyperbolic frequency-modulated bat calls using hyperbolic scale transform | The Journal of the Acoustical Society of America | AIP Publishing

pubs.aip.org 

 

Zhang, Liang, Du, Qinglei

---

July 01 2024

Liang Zhang; Department of Early Warning Technology, Air Force Early Warning Academy, Wuhan, 430019, China

Qinglei Du; Department of Early Warning Technology, Air Force Early Warning Academy, Wuhan,  30019, China

J. Acoust. Soc. Am. 156, 16–28 (2024)

Echolocating bats are known to vary their waveforms at the phases of searching, approaching, and capturing the prey. It is meaningful to estimate the parameters of the calls for bat species identification and the technological improvements of the synthetic systems, such as radar and sonar. The type of bat calls is species-related, and many calls can be modeled as hyperbolic frequency- modulated (HFM) signals. To obtain the parameters of the HFM-modeled bat calls, a reversible integral transform, i.e., hyperbolic scale transform (HST), is proposed to transform a call into two-dimensional peaks in the “delay-scale” domain, based on which harmonic separation and parameter estimation are realized. Compared with the methods based on time-frequency analysis, the HST-based method does not need to extract the instantaneous frequency of the bat calls, only searching for peaks. The verification results show that the HST is suitable for analyzing the HFM-modeled bat calls containing multiple harmonics with a large energy difference, and the estimated parameters imply that the use of the waveforms from the searching phase to the capturing phase is beneficial to reduce the ranging bias, and the trends in parameters may be useful for bat species identification.

I. INTRODUCTION

Bats are well known for their echolocation, like that used in radar and sonar.¹ For example, bats also use transmitted beams,² and the direction can be controlled by moving their head or changing the shape of the mouth or nose. “Advanced” Egyptian fruit bats change the beams by adjusting their tongues,³ similar to the phased array radar. In addition, some issues, such as Doppler compensation,⁴ clutter suppression,⁵ target recognition,⁶ and countermeasures^7,8 are important for both the bats and the synthetic systems. Through over 50 × 10⁶ years of evolution,^9,10 the echolocating bats acquired the capabilities, which actually are more intelligent and efficient than the existing synthetic systems.¹¹ Previous studies have shown that bats vary the waveform during the phases of searching, approaching, and capturing the prey.^12,13 These waveforms are all frequency modulated (FM),^14,15 and many are accurately referred to as the hyperbolic frequency modulated (HFM) signals.^12,16,17 A question naturally arises: “What exactly are the parameters of these waveforms, and how do they change?” This is an interesting but rarely studied subject. This article aims to obtain the parameters of the HFM-modeled bat calls, and explain the waveform strategy from the perspective of correlation detection used in radar and sonar, which may be significant for bat species identification¹⁸ and the design of biomimetic systems.^19,20

To obtain the parameters of HFM-modeled bat calls, it is easy to think of using the existing methods for estimating HFM signal, such as the methods based on group delay (GD) fitting^21,22 and those based on instantaneous frequency (IF) fitting.^23,24 However, the bat calls usually contain multiple harmonics, but GD-based methods require extracting the GD of each component from the spectrum, which is not feasible. In addition, there is a large energy difference between the harmonics, but IF-based methods need to extract the IF of each component from the time-frequency distribution (TFD) of the signal, which is not easy to implement unless a “clean” approach is taken to separate each component,²⁵ just as is done in this paper. Finally, the number of the bat calls may be large, and the estimating process needs to be as simple as possible, for example, the method in this paper only needs a peak search on the proposed hyperbolic scale transform (HST) of a bat call pulse. HST is a linear and reversible transform, capable of transforming an HFM-modeled bat call into several peaks in the “delay-scale” domain and obtaining harmonic parameters according to the peak position. The “delay” above consists of two parts: the first is the time delay of a bat call pulse in the recorded data, and the second is related to a characteristic of the HFM signal, and determined by the model parameters. Of course, if the bat call pulse has been extracted, the first part will be zero. In addition, as a signal processing tool, the proposed HST is not only suitable for the application in this paper but can be used in other fields involving HFM signal processing, such as interference suppression in sonar,²⁶ direction of arrival estimation of wideband signal,²⁷ and so on.

The remainder of the paper is structured as follows. The signal models of the bat call with multiple harmonics are introduced in Sec. II. The HST is proposed in Sec. III, including mathematical definition, property, implementation, and computational complexity. HST-based parameter estimation flow is given in Sec. IV. The performance of HST is validated and discussed using three bat call datasets in Sec. V. A conclusion is drawn in Sec. VI.

II. BAT CALL SIGNAL

To find the optimal Doppler tolerant waveforms, the HFM model is derived in Ref. 16 and found to be used by some bats, such as the long-tailed bat²⁸ and the big brown bat.²⁹ 

A. Model

Considering a $N$-components HFM signal with duration $T$⁠, chirp rate $k_n$⁠, and starting frequency $f_{1,n}$ for the $n$th component $s_n(t)$⁠, the multi-harmonic bat call can be modeled as

$x\left(t\right)=w\left(t\right)\sum _{n=1}^N{A}_n{s}_n\left(t\right)=w\left(t\right)\sum _{n=1}^N{A}_n{\mathrm{e}}^{\mathrm{i}2\pi (1/k_n)\text{ln}\hspace{0.17em}\left[1+k_n{f}_{1,n}t\right]},$(1)

where $t$ is time, $t\in [0,T]$⁠, $w(t)$ is pulse envelope, $N$ is harmonic number, $A_n$ is the amplitude of the $n$th harmonic, $A_1>A_2>\cdots >A_N$⁠, and

where $f_{2,n}$ is the ending frequency, $f_{2,n}<f_{1,n}$⁠, implying a down-sweeping mode. Now, taking the derivative of the phase in Eq. (1) yields the IF of the $n$th harmonic as

which can be expressed as

It can be seen that the IF is a delayed version of $(1/k_n)/t$ with the delay $1/(k_n{f}_{1,n})$⁠. To distinguish the delay of a call pulse in the recorded audio data, $1/(k_n{f}_{1,n})$ is named the intra-pulse delay (IPD) of $n$th harmonic in this paper. The existence of the characteristic is reasonable because $1/(k_{n}t)$ will approach infinity when $t\to 0$⁠, representing a physically impossible signal. The definition of IPD is meaningful because it will affect the ranging bias, if bats adopt correlation detection in the synthetic echolocating systems, which will be illustrated later by analyzing three feeding buzzes. At present, some studies also consider modeling the bat calls, especially the buzz phase calls, as linear frequency modeled (LFM) signals.²⁵ The HFM-modeled bat call signal is closely related to the LFM signal,³⁰ more precisely, the quadratic frequency modulated signal, because the third-order Maclaurin series approximation to the phase of the $n$th harmonic in Eq. (1) is

${\varphi }_n\left(t\right)=2\pi \frac{1}{k_n}\text{ln}\hspace{0.17em}\left[1+k_n{f}_{1,n}t\right]\approx 2\pi [f_{1,n}t-\frac{1}{2}\frac{B_n\left(1-{\xi }_n/2\right)}{T\left(1+{\xi }_n/2\right)}{t}^2-\frac{1}{3}{\xi }_n\frac{B_n\left(1-{\xi }_n/2\right)}{T^2{\left(1+{\xi }_n/2\right)}^2}{t}^3],$

(5)

where $B_n$ is the harmonic bandwidth, $B_n=f_{1,n}-f_{2,n}$⁠, and ${\xi }_n$ is the ratio of the bandwidth to center frequency. When ${\xi }_n$ is small, the third term in the brackets of Eq. (5) can be discarded, then the HFM-modeled bat call degenerates into a LFM-modeled bat call of

$x\left(t\right)=w\left(t\right)\sum _{n=1}^N{A}_n{\mathrm{e}}^{\mathrm{i}2\pi f_{1,n}t}{\mathrm{e}}^{\mathrm{i}\pi {\rho }_n{t}^2},$

(6)

with the starting frequency $f_{1,n}$ and linear chirp rate ${\rho }_n$ of

${\rho }_n=-\frac{B_n\left(1-{\xi }_n/2\right)}{T\left(1+{\xi }_n/2\right)}=-f_{2,n}^2{k}_n,\hspace{1em}{\rho }_n<0.$

(7)

The chirp rate $k_n$ in the HFM model is different from the linear chirp rate ${\rho }_n$ in the LFM model, because $k_n$ has no dimension, while ${\rho }_n$ is usually MHz/s. Because of this, $k_n$ is also named as the modulation index or period slope in some studies.^23,24

B. Spectrum

Different from the waveforms in radar and sonar, there is a modulation in the envelope of the bat call pulse and a solution of the weighted $p$th-order Bessel function leads to the optimal Doppler tolerance.¹⁶ Assuming that $w(t)$ is a rectangular window, the principle of stationary phase can be used to obtain the spectrum of the HFM component $s_n(t)$ of

$S_n\left(f\right)\approx \frac{1}{\sqrt{k_n}}\frac{1}{f}{\mathrm{e}}^{\mathrm{i}2\pi (1/k_n{f}_{1,n})f}{\mathrm{e}}^{\mathrm{i}2\pi (1/k_n)\text{ln}\hspace{0.17em}(f_{1,n}/f)},\hspace{1em}f>0,$

(8)

which is derived in  Appendix A. Then, using the property of the linearity of Fourier transform, the spectrum of the bat call pulse in Eq. (1) is obtained by

$X\left(f\right)=\sum _{n=1}^N{A}_n{S}_n\left(f\right)\approx \sum _{n=1}^N{A}_n\frac{1}{\sqrt{k_n}}\frac{1}{f}{\mathrm{e}}^{\mathrm{i}2\pi (1/k_n{f}_{1,n})f}{\mathrm{e}}^{\mathrm{i}2\pi (1/k_n)\text{ln}\hspace{0.17em}\left(f_{1,n}/f\right)},$

(9)

where the first complex exponent is related to the IPD of $1/(k_n{f}_{1,n})$ and the second is an analytic form of a sine wave about the logarithmic frequency with “frequency” of $1/k_n$⁠. In the following, HST will be designed to compensate for the two terms.

III. HYPERBOLIC SCALE TRANSFORM

If the spectrum in Eq. (9) is considered as a time series, the parameters of the bat call pulse can be obtained by searching the IPD and estimating the “frequency” of the series with “logarithmic time.” Based on the idea, HST is designed below.

A. Mathematical definition

According to the analysis above, the HST of a continuous signal $x(t)$ is defined as

$\begin{array}{c}\text{HST}\left[x\left(t\right)\right]=H_X\left(\tau ,c\right)={\int }_0^{\infty }X\left(f\right){\Upsilon }_{\tau }\left(c,f\right)\mathrm{d}f={\int }_0^{\infty }X\left(f\right)\frac{1}{\sqrt{f}}{\mathrm{e}}^{-\mathrm{i}2\pi f\tau }{\mathrm{e}}^{-\mathrm{i}2\pi c\hspace{0.17em}\text{ln}\hspace{0.17em}f}\mathrm{d}f,\end{array}$

(10)

where HST[·] denotes the HST, $\tau$ is delay, $c$ is scale, a physical attribute like frequency, $X(f)$ is the spectrum of $x(t)$⁠, and ${\Upsilon }_{\tau }(c,f)$ is the kernel functions given by

${\Upsilon }_{\tau }\left(c,f\right)=\frac{1}{\sqrt{f}}{\mathrm{e}}^{-\mathrm{i}2\pi f\tau }{\mathrm{e}}^{-\mathrm{i}2\pi c\hspace{0.17em}\text{ln}\hspace{0.17em}f},$

(11)

in which the first term is used to ensure orthogonality of ${\Upsilon }_{\tau }(c,f)$ about $c$⁠, and the last two terms are designed to match the spectrum in Eq. (9). ${\Upsilon }_{\tau }(c,f)$ satisfy the following relations:

${\int }_{-\infty }^{\infty }{\int }_0^{\infty }{\gamma }_{\tau }^{\ast }\left(c^{\prime },f\right){\gamma }_{\tau }\left(c,f\right)\mathrm{d}f\mathrm{d}\tau =\delta \left(c^{\prime }-c\right),$(12)

${\int }_{-\infty }^{\infty }{\int }_{-\infty }^{\infty }{\gamma }_{\tau }^{\ast }\left(c,f^{\prime }\right){\gamma }_{\tau }\left(c,f\right)\mathrm{d}c\mathrm{d}\tau =\delta \left(f^{\prime }-f\right),$(13)

${\int }_0^{\infty }{\int }_{-\infty }^{\infty }{\gamma }_{{\tau }^{\prime }}^{\ast }\left(c,f\right){\gamma }_{\tau }\left(c,f\right)\mathrm{d}c\mathrm{d}f\ne \delta \left(\tau -{\tau }^{\prime }\right),$(14)

which is derived in  Appendix B. It can be seen that ${\Upsilon }_{\tau }(c,f)$ is not orthogonal about $\tau$⁠, meaning that if the bat call can be transformed into peaks in HST image, the peaks will be a little wider in the delay dimension. The expression of HST is similar to that of scale transform (ST),³¹ a restriction of the $\beta -$ Mellin transform with $\beta =0.5$⁠, and the HST of $x(t)$ is actually the ST of $X(f){\mathrm{e}}^{-\mathrm{i}2\pi f\tau }$⁠. Since ST is reversible, the inverse HST is defined as

$\begin{array}{c}\text{IHST}\left[H_X\left(\tau ,c\right)\right]=X_{\tau }\left(f\right)={\int }_{-\infty }^{\infty }{H}_X\left(\tau ,c\right){\Upsilon }_{\tau }^{\ast }\left(c,f\right)\mathrm{d}c={\int }_{-\infty }^{\infty }{H}_X\left(\tau ,c\right)\frac{1}{\sqrt{f}}{\mathrm{e}}^{\mathrm{i}2\pi f\tau }{\mathrm{e}}^{\mathrm{i}2\pi c\hspace{0.17em}\text{ln}\hspace{0.17em}f}\mathrm{d}c,\end{array}$(15)

where IHST[·] denotes the inverse hyperbolic scale transform, which is the inverse ST of $H_X(\tau ,c){\mathrm{e}}^{\mathrm{i}2\pi f\tau }$⁠. Owing to the orthogonality of ${\Upsilon }_{\tau }(c,f)$ about $c$ and $f$⁠, we can perform scale filtering at a certain $\tau$ and a following inverse Fourier transform leads to the desired time-domain signal. It should be noted that HST also has a certain similarity to the Fourier Mellin transform, commonly used in image processing,³² both calculating the ST of the signal spectrum. However, the phase of the spectrum is retained and modulated in HST, while its modulus is taken in the Fourier Mellin transform to eliminate the delay effect, more conducive to extract the scale-invariant features of the images.³³ 

B. Property analysis

As can be seen from the above analysis, the HST is linear and reversible. To analyze the other properties, the substitution of $x=\text{ln}\hspace{0.17em}f$ into Eq. (10) yields

$H_X\left(\tau ,c\right)={\int }_{-\infty }^{\infty }\sqrt{{\mathrm{e}}^x}X\left({\mathrm{e}}^x\right){\mathrm{e}}^{-\mathrm{i}2{\pi \mathrm{e}}^x\tau }{\mathrm{e}}^{-\mathrm{i}2\pi cx}\mathrm{d}x=F\left[\sqrt{{\mathrm{e}}^x}X\left({\mathrm{e}}^x\right){\mathrm{e}}^{-\mathrm{i}2{\pi \mathrm{e}}^x\tau }\right],$(16)

where F[·] denotes the Fourier transform. The above formula illustrates the relationship between the proposed HST and Fourier transform. Now, according to the properties of Fourier transform, three covariance properties of HST are derived below.

• P1: Time-shift covariance

  $y\left(t\right)=x\left(t-{\tau }_0\right)\Rightarrow Y\left(f\right)=X\left(f\right){\mathrm{e}}^{-\mathrm{i}2\pi f{\tau }_0}\Rightarrow H_Y\left(\tau ,c\right)=H_X\left(\tau +{\tau }_0,c\right).$(17)

  Proof: Let $Y(f)=X(f){\mathrm{e}}^{-\mathrm{i}2\pi f{\tau }_0}$⁠, substituting it into Eq. (16) yields

  $H_Y\left(\tau ,c\right)=F\left[{\mathrm{e}}^{-\mathrm{i}2{\pi \mathrm{e}}^x\left(\tau +{\tau }_0\right)}X\left({\mathrm{e}}^x\right)\sqrt{{\mathrm{e}}^x}\right]=H_X\left(\tau +{\tau }_0,c\right).$(18)

• P2: Time-scaling covariance

  $y\left(t\right)=\sqrt{\beta }x\left(\beta t\right)\Rightarrow Y\left(f\right)=\frac{1}{\sqrt{\beta }}X\left(\frac{f}{\beta }\right)\Rightarrow H_Y\left(\tau ,c\right)={\mathrm{e}}^{-\mathrm{i}2\pi c\hspace{0.17em}\text{ln}\hspace{0.17em}\beta }{H}_X\left(\beta \tau ,c\right).$(19)

  Proof: Let $Y(f)=X(f/\beta )/\sqrt{\beta }$⁠, $\beta >0$⁠, substituting it into Eq. (16) yields

  $\begin{array}{c}{H}_Y\left(\tau ,c\right)=F\left[{\mathrm{e}}^{-\mathrm{i}2{\pi \mathrm{e}}^x\tau }\frac{1}{\sqrt{\beta }}X\left(\frac{{\mathrm{e}}^x}{\beta }\right)\sqrt{{\mathrm{e}}^x}\right]=F\left[{\mathrm{e}}^{-\mathrm{i}2{\pi \mathrm{e}}^{x-\text{ln}\hspace{0.17em}\beta }\beta \tau }\frac{1}{\sqrt{\beta }}X\left({\mathrm{e}}^{x-\text{ln}\hspace{0.17em}\beta }\right)\sqrt{{\mathrm{e}}^{x-\text{ln}\hspace{0.17em}\beta }}\sqrt{{\mathrm{e}}^{\hspace{0.17em}\text{ln}\hspace{0.17em}\beta }}\right]=F\left[{\mathrm{e}}^{-\mathrm{i}2{\pi \mathrm{e}}^{x-\text{ln}\hspace{0.17em}\beta }\left(\beta \tau \right)}X\left({\mathrm{e}}^{x-\text{ln}\hspace{0.17em}\beta }\right)\sqrt{{\mathrm{e}}^{x-\text{ln}\hspace{0.17em}\beta }}\right]={\mathrm{e}}^{-\mathrm{i}2\pi c\hspace{0.17em}\text{ln}\hspace{0.17em}\beta }{H}_X\left(\beta \tau ,c\right).\end{array}$(20)

• P3: Hyperbolic time-shift covariance

  $Y\left(f\right)={\mathrm{e}}^{-\mathrm{i}2\pi c_0\hspace{0.17em}\text{ln}\hspace{0.17em}\left(f/f_1\right)}X\left(f\right)\Rightarrow H_Y\left(\tau ,c\right)={\mathrm{e}}^{\mathrm{i}2\pi c_0\hspace{0.17em}\text{ln}\hspace{0.17em}\left(f_1\right)}{H}_X\left(\tau ,c+c_0\right).$(21)

  Proof: Let $Y(f)=\text{exp}(-\mathrm{i}2\pi c_0\hspace{0.17em}\text{ln}\hspace{0.17em}(f/f_1))X(f)$⁠, substituting it into Eq. (16) yields

  $H_Y\left(\tau ,c\right)=F\left[{\mathrm{e}}^{-\mathrm{i}2{\pi \mathrm{e}}^x\tau }{\mathrm{e}}^{-\mathrm{i}2\pi c_0\hspace{0.17em}\text{ln}\hspace{0.17em}\left({\mathrm{e}}^x/f_1\right)}X\left({\mathrm{e}}^x\right)\sqrt{{\mathrm{e}}^x}\right]={\mathrm{e}}^{\mathrm{i}2\pi c_0\hspace{0.17em}\text{ln}\hspace{0.17em}\left(f_1\right)}{H}_X\left(\tau ,c+c_0\right).$(22)

Remark: The property of P1 is very useful for parameter estimation of bat call, because there may be a delay of the real bat call in the signal extracted from the noisy recordings,³⁴ but this does not affect the accurate estimation of chirp rate. In addition, if the sampling frequency is much greater than the signal bandwidth, the IPD search range can be narrowed by operating time scaling on the bat call pulse according to P2; however, the bat call datasets used in this paper are not the case.

C. Computational complexity

The HST of a continuous signal $x(t)$ is the ST of the modulated spectrum of $X(f){\mathrm{e}}^{-\mathrm{i}2\pi f\tau }$⁠, meaning that a fast numerical calculation can be obtained using fast ST,³⁵ which is equivalent to the description in Eq. (16). Because of the adoption of digital interpolation and fast Fourier transform, the computational complexity of the fast ST can be controlled to a low level of $O[L\hspace{0.17em}\text{ln}\hspace{0.17em}L]$⁠, where $L$ is exponential sample number. According to the exponential sampling theorem,³⁶  $L$ should be not less than $N\hspace{0.17em}\text{ln}\hspace{0.17em}N$⁠, $N$ is the uniform sample number. As to the HST, several times fast ST needs to be calculated for each $\tau$ with a computational complexity of $O[PL\hspace{0.17em}\text{ln}\hspace{0.17em}L]$⁠, where $P$ is the search number of the delay $\tau$ and $L$ is the exponential sample number of $X(f){\mathrm{e}}^{-\mathrm{i}2\pi f\tau }$⁠. Since $X(f){\mathrm{e}}^{-\mathrm{i}2\pi f\tau }$ is the spectrum of $x(t-\tau )$⁠, $L$ should also be not less than $N_1\hspace{0.17em}\text{ln}\hspace{0.17em}{N}_1$⁠, $N_1$ is the sample number of $x(t-\tau )$⁠. Assuming that $N_1$ is slightly larger than $N$⁠, the computational complexity of HST is exactly $O[P(N\hspace{0.17em}\text{ln}\hspace{0.17em}N)\hspace{0.17em}\text{ln}\hspace{0.17em}(N\hspace{0.17em}\text{ln}\hspace{0.17em}N)]$ with a consistent scale resolution of $1/\hspace{0.17em}\text{ln}\hspace{0.17em}{N}_1$⁠. As to the discretization of $\tau$⁠, the delay range and the delay step need to be determined, where the step can be set as a sampling period or more. A larger one implies a coarser delay search and a smaller one indicates a finer search. However, the setting of the delay range depends on the signal parameters. In Sec. IV, we will analyze the HST of the HFM-modeled bat call pulse and give a reasonable solution.

IV. PARAMETER ESTIMATION

Bat calls often contain several harmonics with large energy differences. It is difficult to obtain the parameters of each harmonic by calculating HST only once, because of the masking effect of strong harmonics on weak harmonics, so it is necessary to use inverse HST to filter out the strong harmonics before estimating the parameters of weak harmonics. Based on this idea, this section will give an estimation flow using HST and inverse HST, and demonstrate the advantages of the proposed method mathematically by analyzing the limitations of the existing estimation methods.

A. Proposed method

The design of the kernel functions in HST is to compensate for the exponent terms in the signal spectrum. Now, substituting Eq. (9) into Eq. (10) yields the HST of a bat call pulse as

where $H_{S_n}(\tau ,c)$ is the HST of the $n$th HFM component, and

$H_{S_n}\left(\tau ,c\right)=\left(\frac{1}{\sqrt{k_n}}{\mathrm{e}}^{\mathrm{i}2\pi (1/k_n)\text{ln}\hspace{0.17em}{f}_{1,n}}\right){\int }_{f_{1,n}}^{f_{2,n}}\frac{1}{\sqrt{f}}{\mathrm{e}}^{\mathrm{i}2\pi \left((1/k_n{f}_{1,n})-\tau \right)f}{\mathrm{e}}^{-\mathrm{i}2\pi \left((1/k_n)+c\right)\hspace{0.17em}\text{ln}\hspace{0.17em}f}\mathrm{d}\left(\text{ln}\hspace{0.17em}f\right)\approx \delta \left(\tau -\frac{1}{k_n{f}_{1,n}}\right)\delta \left(c+\frac{1}{k_n}\right),$(24)

which approximates a two-dimensional (2D) peak at the peak delay ${\tau }_{\mathrm{p}}$ and the peak scale $c_{\mathrm{p}}$ of

It can be seen that ${\tau }_{\mathrm{p}}$ is equal to the IPD of $n$th harmonics and $c_{\mathrm{p}}$ is related to the reciprocal of the chirp rate. In particular, when $\tau ={\tau }_{\mathrm{p}}$⁠, Eq. (24) can be approximated as

$H_{S_n}\left({\tau }_{\mathrm{p}},c\right)\approx \left(\frac{1}{\sqrt{k_n}}{\mathrm{e}}^{\mathrm{i}2\pi (1/k_n)\text{ln}\hspace{0.17em}{f}_{1,n}}\right)\hspace{0.17em}\text{ln}\hspace{0.17em}\left(\frac{f_{2,n}}{f_{1,n}}\right)\text{sinc}\left\{\pi \hspace{0.17em}\text{ln}\hspace{0.17em}\left(\frac{f_{2,n}}{f_{1,n}}\right)\left(c+1/k_n\right)\right\},$(26)

where sinc[·] denotes the sinc function. Then, the parameters of $n$th harmonic can be estimated by

There are two issues to be noted here. First, to ensure the presence of peaks in HST, the delay search range needs to cover all the intra-pulse delays (IPDs) of the harmonics. According to the expression of the chirp rate in Eq. (2), the peak delay ${\tau }_{\mathrm{p}}$ of $n$th harmonics can be exactly expressed as

${\tau }_{\mathrm{p}}=\frac{1}{k_n{f}_{1,n}}=T\frac{f_{2,n}}{f_{1,n}-f_{2,n}}.$(28)

Since most of the bat calls are down-sweeping, i.e., ${\tau }_{\mathrm{p}}>0$⁠, meaning that the minimum delay $d_{\text{min}}$ can be set to 0, but the maximum delay $d_{\text{max}}$ is not easy to determine, as ${\tau }_{\mathrm{p}}$ tends to infinity theoretically, if $f_{1,n}$ is close to $f_{2,n}$⁠. The situation usually does not happen, and an empirical setting of $d_{\text{max}}$ of three times the signal duration is sufficient. In addition, there is a large energy difference between the harmonics, resulting in a masking of the strong harmonics on the weak harmonics in the “delay-scale” domain, so it is necessary to estimate the parameters of the strongest harmonic first by searching the highest 2D peak in HST image of a bat call, according to Eq. (27), then with a “clean” approach to estimate the parameters of the sub-strong harmonic from the HST image of the signal after scale filtering, and so on. As to the bat call $x(t)$⁠, the filtered signal can be expressed as

$\begin{array}{c}\tilde{x}\left(t\right)=x\left(t\right)-F^{-1}\left\{\text{IHST}\left[\text{HST}\left[x\left(t\right)\right]\Gamma \left(c\right)\right]\right\}=x\left(t\right)-{\mathrm{F}}^{-1}\left\{{\text{ST}}^{-1}\left[\text{ST}\left[F\left[x\left(t\right)\right]{\mathrm{e}}^{-\mathrm{i}2\pi f{\tau }_{\mathrm{p}}};c\right]\Gamma \left(c\right);f\right]\right\},\end{array}$(29)

where F⁻¹[·], ST[·] and ST⁻¹[·] denote inverse Fourier transform, ST, and inverse ST, respectively, and $\Gamma (c)$ is a rectangular window with the center at $c_{\mathrm{p}}$ and width set to cover the main-lobe width of the sinc function in Eq. (26). As the analysis above, Table I shows the parameter estimation flow for the harmonics within a bat call pulse, where the bat call pulse is extracted from the recorded data, and the number of harmonics to be estimated is set by yourself. The reliability of this process is closely related to the extraction of effective pulses, which involves bat signal detection.³⁴ 

TABLE I.

HST and inverse HST are used to estimate the harmonic parameters of a bat call pulse.

Input: Bat call pulse $x(t)$⁠, minimum delay $d_{\text{min}}$⁠, maximum delay $d_{\text{max}}$⁠, and harmonic number $N$

1) Calculate Fourier transform of $x(t)$⁠, and get its spectrum $X(f)$⁠.

2) Calculate HST of $X(f)$⁠, and get $H_X(\tau ,c)$⁠, $\tau \in [d_{\text{min}},d_{\text{max}}]$⁠.

3) Search the maximum of $\left|H_X(\tau ,c)\right|$⁠, and obtain the peak delay ${\tau }_{\mathrm{p}}$ and the peak scale $c_{\mathrm{p}}$⁠.

4) Estimate the chirp rate $k_n$ and the starting frequency $f_{1,n}$ according to Eq. (27).

5) Filter out the strongest harmonic of $x(t)$ through Eq. (29), and get the filtered signal.

6) Repeat steps 1–5 until the parameters of $N$ harmonics have been estimated.

Output: The estimated chirp rate $k_n$ and starting frequency $f_{1,n}$⁠, $n=1,2,\dots ,N$

Input: Bat call pulse $x(t)$⁠, minimum delay $d_{\text{min}}$⁠, maximum delay $d_{\text{max}}$⁠, and harmonic number $N$

1) Calculate Fourier transform of $x(t)$⁠, and get its spectrum $X(f)$⁠.

2) Calculate HST of $X(f)$⁠, and get $H_X(\tau ,c)$⁠, $\tau \in [d_{\text{min}},d_{\text{max}}]$⁠.

3) Search the maximum of $\left|H_X(\tau ,c)\right|$⁠, and obtain the peak delay ${\tau }_{\mathrm{p}}$ and the peak scale $c_{\mathrm{p}}$⁠.

4) Estimate the chirp rate $k_n$ and the starting frequency $f_{1,n}$ according to Eq. (27).

5) Filter out the strongest harmonic of $x(t)$ through Eq. (29), and get the filtered signal.

6) Repeat steps 1–5 until the parameters of $N$ harmonics have been estimated.

Output: The estimated chirp rate $k_n$ and starting frequency $f_{1,n}$⁠, $n=1,2,\dots ,N$

B. Traditional estimation methods

Parameter estimation of the HFM-modeled bat calls can be considered a special case of HFM signal parameter estimation. As mentioned in Sec. I, the GD-based methods^21,22 for parameter estimation of the mono-component HFM signal are not feasible because the bat calls usually contain multiple harmonics, while the IF-based methods^23,24 seem to be feasible, but require more human assistance to obtain the IF of each harmonic, which is not suitable for a large number of bat calls. In addition, some studies try to use Q distribution and fractional Fourier transform (FRFT) for bat call analysis.^25,37 Below, we will analyze their feasibility for parameter estimation.

Q distribution, representing a signal in the “time-scale” domain, is used to analyze the scale domain characteristics of a bat pulse (Eptesicus focus), finding that there is a quadratic phase coupling between the harmonics.³⁷ The Q distribution of the continuous signal $x(t)$ is defined as

$Q_x\left(t,c\right)={\int }_0^{\infty }x\left(\sqrt{a}t\right)x^{\ast }\left(\frac{1}{\sqrt{a}}t\right)\frac{1}{a}{\mathrm{e}}^{-\mathrm{i}2\pi c\hspace{0.17em}\text{ln}\hspace{0.17em}a}\mathrm{d}a,$(30)

where $a$ is the time-scaling factor. It can be seen that the expression of Q distribution is also similar to that of the ST, with the relationship of

$Q_x\left(t,c\right)=\text{ST}\left[\frac{1}{\sqrt{a}}x\left(\sqrt{a}t\right)x^{\ast }\left(\frac{1}{\sqrt{a}}t\right);c\right].$(31)

Substituting Eq. (1) into Eq. (31) yields the Q distribution of an HFM-modeled bat call as

$Q_x\left(t,c\right)=\sum _{n=1}^N{Q}_{\text{auto}}^{\left(n\right)}\left(t,c\right)+Q_{\text{cross}}\left(t,c\right),$(32)

where $Q_{\text{auto}}^{(n)}(t,c)$ is the auto-term of the $n$th harmonic with the expression of

$Q_{\text{auto}}^{\left(n\right)}\left(t,c\right)=A_n^2\text{ST}[\frac{1}{\sqrt{a}}{\mathrm{e}}^{\mathrm{i}2\pi (1/k_n)\text{ln}\hspace{0.17em}a}{\mathrm{e}}^{\mathrm{i}2\pi (1/k_n)\text{ln}\hspace{0.17em}[\left(t+(1/\sqrt{a})(1/k_n{f}_{1,n})\right)/\left(t+\sqrt{a}(1/k_n{f}_{1,n})\right)]};c],$(33)

and $Q_{\text{cross}}(t,c)$ denotes the cross terms caused by the bilinear character of Q distribution. Assuming that the IPDs of harmonics are all zeros, the auto-term can be further expressed as

$Q_{\text{auto}}^{\left(n\right)}\left(t,c\right)=A_n^2{\mathrm{e}}^{\mathrm{i}2\pi (1/k_n)t}\text{ST}\left[\frac{1}{\sqrt{a}}{\mathrm{e}}^{\mathrm{i}2\pi (1/k_n)\text{ln}\hspace{0.17em}a};c\right]\approx A_n^2{\mathrm{e}}^{\mathrm{i}2\pi (1/k_n)t}\delta \left(c-\frac{1}{k_n}\right),$(34)

which is not a 2D peak, but a perpendicular about $t$⁠, and can be understood as instantaneous scale. Since the IPDs of harmonics are not zeros, multiple time-shifts plus the calculation of Q distribution for a bat call pulse are required.³⁷ The IPDs of harmonics may be not the same, then the treatment will be effective for the pulse with only a harmonic. In addition, the instantaneous scale of the HFM-modeled is constant, meaning that Q function is more suitable for analyzing signal forms with scale modulation. As mentioned in Sec. II A, if the ratio of harmonic bandwidth to center frequency is small, the HFM-modeled bat call in Eq. (1) will degenerate into a LFM-modeled bat call as

$x\left(t\right)=w\left(t\right)\sum _{n=1}^N{A}_n{\mathrm{e}}^{\mathrm{i}2\pi f_{1,n}t}{\mathrm{e}}^{\mathrm{i}\pi {\rho }_n{t}^2},$(35)

then FRFT is a good option for analysis.²⁵ When the rotation angle $b\ne n\pi$⁠, and $n$ is an integer, the continuous FRFT is defined by

$X_p\left(u\right)={\mathrm{e}}^{\mathrm{i}\pi \text{cot}b{u}^2}\sqrt{1-\mathrm{i}\text{cot}b}{\int }_{-\infty }^{+\infty }s\left(t\right){\mathrm{e}}^{-\mathrm{i}2\pi \csc \mathit{\text{but}}}{\mathrm{e}}^{\mathrm{i}\pi \text{cot}b{t}^2}\mathrm{d}t,$(36)

where $p$ is order, $p=b/(\pi /2)$⁠, and $u$ denotes the fractional domain or $u$ domain. Now, setting $p$ as the optimal order $p_n=2\mathrm{a}\text{cot}(-{\rho }_n)/\pi$⁠, the FRFT modulus of the LFM-modeled bat call is

$X_{p_n}u\approx \sum _{n=1}^N{A}_n\sqrt{1+i{\rho }_n}\delta u-f_{1,n}\hspace{0.17em}\text{sin}\hspace{0.17em}\frac{\pi }{2}{p}_{p_n}.$(37)

Since $p_n$ is unknown, an order search can ensure that the LFM-modeled call is transformed into 2D peaks, whose number is the same as that of the harmonics, as shown in Fig. 1. Assuming that a peak is at $(p_n,u_n)$⁠, the parameters of the $n$th harmonic can be estimated by

$\{\begin{array}{c}{f}_{1,n}=u_n\hspace{0.17em}\text{csc}\left(p_n\pi /2\right),\\ {\rho }_n=-\text{cot}\left(p_n\pi /2\right).\end{array}$(38)

Consistent with the proposed HST, FRFT is also reversible, just adjusting $p$ to $-p$ in Eq. (36), so the idea in Table I is applicable to FRFT, i.e., estimating the parameters of the strongest harmonic first, filtering out the harmonic, and then estimating the parameters of the weak harmonics. However, there is a prerequisite for the effectiveness of the idea, i.e., the FM modes of the harmonics should be as linear as possible, otherwise, the broadened peaks will affect the parameter estimation accuracy of the strong harmonic, and the weak harmonic parameters cannot be accurately estimated because the strong harmonic cannot be completely filtered out. Based on the analysis, we can conclude that Q distribution is not suitable for parameter estimation of the bat calls, and FRFT is, but requires a linear FM bat call. Comparatively, the proposed method does not have the limitation.

FIG. 1.

(Color online) A call pulse emitted by the big brown bat (Eptesicus fuscus). (a) Time-frequency distribution. (b) FRTF.

FIG. 1.

(Color online) A call pulse emitted by the big brown bat (Eptesicus fuscus). (a) Time-frequency distribution. (b) FRTF.

Close modal

V. VALIDATION AND DISCUSSION

When searching, approaching, and capturing the prey, the bats emit a series of pulses. In the section, the harmonic parameters of the bat call pulses are estimated according to the flow in Table I, on the basis of which the waveform strategy is discussed.

A. Bat call data

The bat call data required in this paper can be obtained on the Internet without the need for an experiment. For example, Avisoft Bioacoustics Company (Nordbahn, Germany) provides many types of bat calls, including social calls, distress calls, and feeding buzzes from various European bats (see Data Availability). In this paper, feeding buzzes from the three bat species are selected as the processing objects, as shown in Fig. 2. The duration of the first dataset is about 220 ms and that of the other two is about 500 ms, with a sampling frequency of 250 kHz. It should be noted that only the third dataset includes the search phase, while the first and second datasets relate to the approach and capturing phases. According to the time-frequency distributions (TFDs) below the data in time domain, it can be seen that these calls are all down-sweeping, and most of them exhibit the HFM characteristics. Since the sample size reaches 10⁴, 83 bat call pulses are extracted and shown in Fig. 3.

FIG. 2.

(Color online) Bat call datasets. (a) First data from the bat (Nyctalus noctula). (b) Second data from the bat (Pipistrellus pipistrellus). (c) Third data from the bat (Pipistrellus pygmaeus).

FIG. 2.

(Color online) Bat call datasets. (a) First data from the bat (Nyctalus noctula). (b) Second data from the bat (Pipistrellus pipistrellus). (c) Third data from the bat (Pipistrellus pygmaeus).

Close modal

FIG. 3.

(Color online) The extracted call pulses. (a) 17 pulses from the first dataset. (b) 40 pulses from the second dataset. (c) 26 pulses from the third dataset.

FIG. 3.

(Color online) The extracted call pulses. (a) 17 pulses from the first dataset. (b) 40 pulses from the second dataset. (c) 26 pulses from the third dataset.

Close modal

For a better display effect, a zeros-padding operation is performed at both ends of the pulses, but this is not the case when they are calculated. The sample size of the bat pulses varies greatly, with the maximum being close to 1000 and the minimum being less than 100. The pulses in the first two phases usually contain two harmonics, and the three-harmonic pulses are used at the capturing phase, so only the first and second harmonics are considered for estimation in Sec. V B.

B. Validation

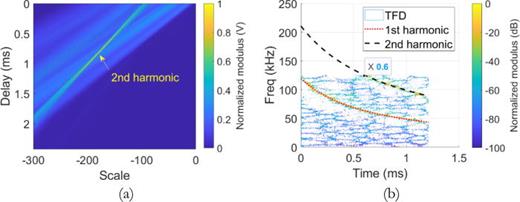
In this section, we first verify the feasibility of the parameter estimation flow in Table I with a bat pulse, and then apply the processing to all pulses along with a comparison with the estimation using FRFT. Setting the delay range to 0∼3 times the duration of the pulse and a step of a sampling period, the waveform of the 10th pulse from the second dataset and its HST are shown in Fig. 4. A 2D spectral peak with a delay of 0.69 ms and a scale of –81.9 is found in the HST image. According to Eq. (27), the starting frequency and chirp rate of the first harmonic are estimated as 119.22 kHz and 0.0122, respectively. To estimate the parameters of the second harmonic, a red-marked window is set to filter out the first harmonic, and using Eq. (29), the filtered signal is obtained, as shown in Fig. 5.

FIG. 4.

(Color online) Parameter estimation of the first harmonic. (a) Waveform of the bat call pulse. (b) HST of the pulse.

FIG. 4.

(Color online) Parameter estimation of the first harmonic. (a) Waveform of the bat call pulse. (b) HST of the pulse.

Close modal

FIG. 5.

(Color online) Performing scaling filtering. (a) Scaling filter. (b) The filtered signal.

FIG. 5.

(Color online) Performing scaling filtering. (a) Scaling filter. (b) The filtered signal.

Close modal

Finally, the HST of the filtered signal is calculated as shown in Fig. 6(a). There is also a peak in the HST image, but it is significantly broadened in the delay dimension. According to the peak position, the starting frequency and chirp rate of the second harmonic are estimated as 210.61 kHz and 0.0054, respectively. As shown in Fig. 6(b), we plot the estimated instantaneous frequencies (IFs) calculated by Eq. (3) on the high-resolution TFD obtained by performing reassignment on the short-time Fourier transform of the signal.³⁸ It can be seen that the estimated IF curves indeed coincide with the real IFs. There are two issues worth noting. First, the harmonic energy of the bat call pulse varies greatly, and we cannot estimate the parameters of all harmonics by calculating HST only once, implying that scale filtering in Table I is necessary. In addition, there is a delay of 0.6 ms for the second harmonic in the pulse, resulting in the estimated starting frequency of 210.61 kHz being unreliable, but the chirp rate can be accurately estimated, consistent with the analysis in Sec. III A. Theoretically, we can roughly estimate the delay of the second harmonic by looking at the TFD of the pulse, but this workload is very large for many pulses, so the estimation of the starting frequency of the second harmonic will not be considered below.

FIG. 6.

(Color online) Parameter estimation of second harmonic (a) HST of the filtered signal. (b) Estimated instantaneous frequencies of the two harmonics.

FIG. 6.

(Color online) Parameter estimation of second harmonic (a) HST of the filtered signal. (b) Estimated instantaneous frequencies of the two harmonics.

Close modal

Based on the processing above, the parameters of the 83 pulses are estimated. According to the parameter curves of the first harmonic in Fig. 7, it can be seen that the bats are always increasing the chirp rate of the first harmonic when searching, approaching, and capturing the prey, but the starting frequency is not adjusted in this way. In general, a high starting frequency is used in the middle phase, while a low starting frequency is adopted in the other two phases. An interesting phenomenon is that the parameter curves of the second dataset are closer to those of the third dataset, indicating that the HST may be useful in bat species identification, because the last two datasets are from the same species. However, such identification may not be achieved by analyzing only a pulse, but needing the analysis of multiple pulses and then performing a comparison of the parameter curves.

FIG. 7.

(Color online) Parameter estimation of first harmonic of the HFM-modeled bat call pulses using the proposed method. (a) Peak delay. (b) Peak scale. (c) Starting frequency. (d) Chirp rate.

FIG. 7.

(Color online) Parameter estimation of first harmonic of the HFM-modeled bat call pulses using the proposed method. (a) Peak delay. (b) Peak scale. (c) Starting frequency. (d) Chirp rate.

Close modal

The second harmonic has a known delay in the extracted pulses, resulting in the estimated starting frequency being unreliable according to the property of time-shift covariance of HST, although not erroneous, so only the chirp rate is estimated in Fig. 8. The trend is the same as that of the first harmonic, but the values are smaller. In addition, there are significant jumps in the estimated curves, indicating that the estimation is not good. There are two reasons to explain it: one is that the energy of the second harmonic is too weak and the sample size is smaller, and the second is that the signal-to-noise ratio of the filtered signal is low. In general, the estimation of the first harmonic is reliable for analysis, while that of the second harmonic is inclined to be used as a reference.

FIG. 8.

(Color online) Parameter estimation of second harmonic of the HFM-modeled bat call pulses using the proposed method. (a) Peak scale. (b) Chirp rate.

FIG. 8.

(Color online) Parameter estimation of second harmonic of the HFM-modeled bat call pulses using the proposed method. (a) Peak scale. (b) Chirp rate.

Close modal

To demonstrate the advantages of the proposed HST, a parameter estimation comparison with FRFT is necessary. Here, only the parameters of the first harmonics, i.e., the strongest harmonic, are taken into account. Setting the FRFT orders from 0 to 2, the starting frequency and the linear chirp rate of the first harmonic in the 83 pulses are estimated and shown in Fig. 9. In general, the estimation of the starting frequency is similar to that in Fig. 7(c), and the trend of the modulus of the linear chirp rate is also the same as that in Fig. 7(d), which is consistent with Eq. (7).

FIG. 9.

(Color online) Parameter estimation of the first harmonic of the bat call pulses using FRTF. (a) Starting frequency. (b) Linear chirp rate.

FIG. 9.

(Color online) Parameter estimation of the first harmonic of the bat call pulses using FRTF. (a) Starting frequency. (b) Linear chirp rate.

Close modal

However, the estimated starting frequency of the fifth through eighth pulses in Fig. 9(a) is anomalous, because they exceed 0.5 times sampling frequency, i.e., 125 kHz. To find the cause of the problem, we select the eighth and ninth pulses as processing objects, use FRFT and HST to estimate the parameters of the first harmonic, respectively, and then plot the estimated IFs to their TFD, as shown in Figs. 10 and 11. For the eighth pulse, the harmonic corresponding to the FRFT maximum peak is not the first harmonic, but the second harmonic, meaning that the estimated starting frequency of the fifth through eighth pulse in Fig. 9(a) is that of the second harmonic. In other words, FRFT is more suitable for estimating the parameters of the bat calls containing only a harmonic. In contrast, the proposed HST does not have such a problem. In addition, the estimated parameter curves using HST appear to be smoother, especially the curves of the peak scale and peak delay in Figs. 7(a) and 7(b).

FIG. 10.

(Color online) The estimated IFs obtained by FRFT. (a) Eighth bat call. (b) Ninth bat call.

FIG. 10.

(Color online) The estimated IFs obtained by FRFT. (a) Eighth bat call. (b) Ninth bat call.

Close modal

FIG. 11.

(Color online) The estimated IFS obtained by HST. (a) Eighth bat call. (b) Ninth bat call.

FIG. 11.

(Color online) The estimated IFS obtained by HST. (a) Eighth bat call. (b) Ninth bat call.

Close modal

C. Discussion

In this section, we try to explain the waveform strategy using the wideband ambiguity function. The wideband ambiguity function (WAF) of the waveform $s(t)$ is defined in the frequency domain as

${\text{WAF}}_S\left(\alpha ,\tau \right)={\int }_{-\infty }^{\infty }S\left(f\right)\frac{1}{\sqrt{\alpha }}{S}^{\ast }\left(\frac{f}{\alpha }\right){\mathrm{e}}^{\mathrm{i}2\pi f\tau }\mathrm{d}f,$

(39)

where $S(f)$ is the spectrum of $s(t)$⁠, $\alpha$ is the Doppler compression factor, $\alpha =(\mathrm{c}+v)/(\mathrm{c}-v)$⁠, $\mathrm{c}$ is the speed of sound, and $v$ is the relative velocity between the bat and its prey. Substituting Eq. (8) into Eq. (39) yields the wideband ambiguity function of the $n$th harmonic as

${\text{WAF}}_{S_n}\left(\alpha ,\tau \right)={\mathrm{e}}^{-\mathrm{i}2\pi (1/k_n)\text{ln}\hspace{0.17em}\left(\alpha \right)}\frac{1}{\sqrt{\alpha }{k}_n}{\int }_{f_{1,n}}^{f_{2,n}}\frac{1}{f^2}{\mathrm{e}}^{\mathrm{i}2\pi \alpha -1/\alpha 1/k_n{f}_{1,n}f}\mathrm{d}f,$

(40)

with the maximum value at

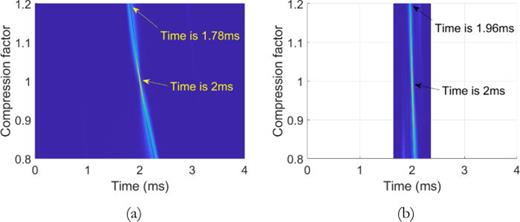
it can be seen that there is an unavoidable ranging bias, which is proportional to the IPD.³⁹ Since the Doppler compression factor is related to the sound speed and the relative velocity between the bat and prey, the adoption of decreasing IPD will be beneficial to reduce the ranging bias, as shown in Fig. 12. As to the first and 17th pulse in first dataset, when the factor is 1.2, i.e., the relative velocity between the bat and its prey is about 30 m/s with the speed of sound of 340 m/s, the bias of the first pulse observed from the WAF plot is about 0.22 ms, while that of the 17th pulse is only 0.04 ms. Because the parameters of the bat call pulse are set depending on the particular task to be carried out, it is easier to capture the target using the waveforms with higher-ranging accuracy if the target has already been judged to be the prey. The conclusion above has been made for a long time,¹² but not been supported by the estimated parameters so far, meaning that the results in this paper are significant. It must be admitted that the bats may not employ correlation detection used in the synthetic systems of radar and sonar, but a complex technique or model;⁴⁰ however, the analysis above is still meaningful for the improvement of the biomimetic technologies.

FIG. 12.

(Color online) Wideband ambiguity function. (a) First pulse. (b) 17th pulse.

FIG. 12.

(Color online) Wideband ambiguity function. (a) First pulse. (b) 17th pulse.

Close modal

VI. CONCLUSION

To estimate the parameters of the HFM-modeled bat calls, this paper proposes a transform, namely HST. HST is a linear and reversible transform with the properties of time-shift covariance, time-scaling covariance, and so on, very suitable for harmonic separation and parameter estimation of the HFM-modeled bat calls. The performance of HST is verified by three bat call datasets, and the estimated parameters show that bats are always increasing the chirp rate of the harmonics when searching, approaching, and capturing the prey, meaning that bats are very concerned about the ranging accuracy of the waveforms, which is consistent with the radar—sonar–related theory. In addition, the high starting frequency is often used in the approaching phase, while the low starting frequency is adopted in the other two phases. It should be noted that the IPD of the HFM-modeled bat calls is larger in the first phases, requiring a large delay range when HST is calculated. To reduce the computational amount, an idea is to take a large step for coarse search, and then take a small step for fine search. Future research is to apply HST to analyze the HFM-like calls of other mammals,⁴¹ as well as to the areas involving HFM signal processing.

ACKNOWLEDGMENTS

This work was supported by the National Natural Science Foundation of China (Grant Nos. 62101593, 62271498, and 62101583).

AUTHOR DECLARATIONS

Conflict of Interest

The authors have no conflicts to disclose.

DATA AVAILABILITY

APPENDIX A

The expression of the $n$th HFM component is

$s_{n}t=e^{i2\pi (1/k_n)\mathit{\text{ln}}1+k_n{f}_{1,n}t},$(A1)

assuming that the duration of $s_n(t)$ is infinite. According to the principle of stationary phase, first taking the integral phase term of the Fourier transform of $s_n(t)$ yields

$\varphi \left(t,f\right)=2\pi \hspace{0.17em}\text{ln}\hspace{0.17em}\left(1+k_n{f}_{1,n}t\right)/k_n-2\pi ft,$(A2)

its derivatives are given by

${\varphi }^{\prime }\left(t,f\right)=2\pi /\left[t+1/\left(k_n{f}_{1,n}\right)\right]k_n-2\pi f,$(A3)

${\varphi }^{″}\left(t,f\right)=-2\pi /{\left[t+1/\left(k_n{f}_{1,n}\right)\right]}^2{k}_n.$(A4)

Setting ${\varphi }^{\prime }(t,f)=0$⁠, the stationary point $t_0$ is obtained as

Finally, the spectrum of $s_n(t)$ is derived as

$S_n\left(f\right)\approx \left({\mathrm{e}}^{\mathrm{i}\frac{3}{4}\pi }{\mathrm{e}}^{-\mathrm{i}2\pi (1/k_n)}\frac{1}{2\sqrt{k_n}}\right)\frac{1}{f}{\mathrm{e}}^{\mathrm{i}2\pi (1/k_n{f}_{1,n})f}{\mathrm{e}}^{\mathrm{i}2\pi (1/k_n)\text{ln}\hspace{0.17em}\left(f_{1,n}/f\right)},\hspace{1em}f>0,$(A6)

where the first part is a complex constant, the second part implies that the spectrum envelope is inversely proportional to frequency $f$⁠, and the third part is a product of two complex exponents.

APPENDIX B

The kernel functions of the HST are

${\Upsilon }_{\tau }\left(c,f\right)=\frac{1}{\sqrt{f}}{\mathrm{e}}^{-\mathrm{i}2\pi f\tau }{\mathrm{e}}^{-\mathrm{i}2\pi c\hspace{0.17em}\text{ln}\hspace{0.17em}f},$(B1)

where $\tau$ is delay, $c$ is scale, and $f$ is frequency. The orthogonality of the HST can be obtained according to the double integrals below:

$\begin{array}{c}{\int }_{-\infty }^{\infty }{\int }_0^{\infty }{\gamma }_{\tau }^{\ast }\left(c^{\prime },f\right){\gamma }_{\tau }\left(c,f\right)\mathrm{d}f\mathrm{d}\tau ={\int }_{-\infty }^{\infty }{\int }_0^{\infty }\frac{1}{\sqrt{f}}{\mathrm{e}}^{\mathrm{i}2\pi f\tau }{\mathrm{e}}^{\mathrm{i}2\pi c^{\prime }\hspace{0.17em}\text{ln}\hspace{0.17em}f}\frac{1}{\sqrt{f}}{\mathrm{e}}^{-\mathrm{i}2\pi f\tau }{\mathrm{e}}^{-\mathrm{i}2\pi c\hspace{0.17em}\text{ln}\hspace{0.17em}f}\mathrm{d}f\mathrm{d}\tau ={\int }_{-\infty }^{\infty }\mathrm{d}\tau {\int }_0^{\infty }{\mathrm{e}}^{\mathrm{i}2\pi \left(c^{\prime }-c\right)\hspace{0.17em}\text{ln}\hspace{0.17em}f}\mathrm{d}\left(\text{ln}\hspace{0.17em}f\right)=\delta \left(c^{\prime }-c\right),\end{array}$(B2)

$\begin{array}{c}{\int }_{-\infty }^{\infty }{\int }_{-\infty }^{\infty }{\gamma }_{\tau }^{\ast }\left(c,f^{\prime }\right){\gamma }_{\tau }\left(c,f\right)\mathrm{d}c\mathrm{d}\tau ={\int }_{-\infty }^{\infty }{\int }_{-\infty }^{\infty }\frac{1}{\sqrt{f^{\prime }}}{\mathrm{e}}^{\mathrm{i}2\pi f^{\prime }\tau }{\mathrm{e}}^{\mathrm{i}2\pi c\hspace{0.17em}\text{ln}\hspace{0.17em}{f}^{\prime }}\frac{1}{\sqrt{f}}{\mathrm{e}}^{-\mathrm{i}2\pi f\tau }{\mathrm{e}}^{-\mathrm{i}2\pi c\hspace{0.17em}\text{ln}\hspace{0.17em}f}\mathrm{d}c\mathrm{d}\tau ={\int }_{-\infty }^{\infty }{\mathrm{e}}^{\mathrm{i}2\pi \left(f^{\prime }-f\right)\tau }\mathrm{d}\tau \frac{1}{\sqrt{f}\sqrt{f^{\prime }}}{\int }_{-\infty }^{\infty }{\mathrm{e}}^{\mathrm{i}2\pi \left(\text{ln}\hspace{0.17em}{f}^{\prime }-\text{ln}\hspace{0.17em}f\right)c}\mathrm{d}c=\delta \left(f^{\prime }-f\right),\end{array}$(B3)

$\begin{array}{c}{\int }_0^{\infty }{\int }_{-\infty }^{\infty }{\gamma }_{{\tau }^{\prime }}^{\ast }\left(c,f\right){\gamma }_{\tau }\left(c,f\right)\mathrm{d}c\mathrm{d}f={\int }_0^{\infty }{\int }_{-\infty }^{\infty }\frac{1}{\sqrt{f}}{\mathrm{e}}^{\mathrm{i}2\pi f{\tau }^{\prime }}{\mathrm{e}}^{\mathrm{i}2\pi c\hspace{0.17em}\text{ln}\hspace{0.17em}f}\frac{1}{\sqrt{f}}{\mathrm{e}}^{-\mathrm{i}2\pi f\tau }{\mathrm{e}}^{-\mathrm{i}2\pi c\hspace{0.17em}\text{ln}\hspace{0.17em}f}\mathrm{d}c\mathrm{d}f={\int }_{-\infty }^{\infty }\mathrm{d}c{\int }_0^{\infty }\frac{1}{f}{\mathrm{e}}^{\mathrm{i}2\pi \left({\tau }^{\prime }-\tau \right)f}\mathrm{d}f\ne \delta \left(\tau -{\tau }^{\prime }\right).\end{array}$(B4)

REFERENCES

1. M. Denny, “  The physics of bat echolocation: Signal processing techniques,”  Am. J. Phys. 72,  1465 – 1477 ( 2004 ).

2. K. Ghose and  C. F. Moss, “  The sonar beam pattern of a flying bat as it tracks tethered insects,”  J. Acoust. Soc. Am. 114,  1120 – 1131 ( 2003 ).

3. W. J. Lee,  B. Falk, and  C. Chiu, “  Tongue-driven sonar beam steering by a lingual-echolocating fruit bat,”  PLoS Biol. 15,  e2003148 ( 2017 ).

4. D. Schoeppler,  H. U. Schnitzler, and  A. Denzinger, “  Precise Doppler shift compensation in the hipposiderid bat, Hipposideros armiger,”  Sci. Rep. 8,  1 – 11 ( 2018 ).

5. M. E. Bates,  J. A. Simmons, and  T. V. Zorikov, “  Bats use echo harmonic structure to distinguish their targets from background clutter,”  Science 333,  627 – 630 ( 2011 ).

6. S. Uday and  J. A. Simmons, “  Echolocating bats perceive natural-size targets as a unitary class using micro-spectral ripples in echoes,”  Behav. Neurosci. 133,  297 – 304 ( 2019 ).

7. B. C. Leavell,  J. J. Rubin,  C. J. McClure,  K. A. Miner,  M. A. Branham, and  J. R. Barber, “  Fireflies thwart bat attack with multisensory warnings,”  Sci. Adv. 4,  eaat6601 ( 2018 ).

8. J. J. Rubin,  C. A. Hamilton,  J. W. McClure,  B. A. Chadwell,  A. Y. Kawahara, and  J. R. Barber, “  The evolution of anti-bat sensory illusions in moths,”  Sci. Adv. 4,  eaar7428 ( 2018 ).

9. E. C. Teeling,  M. Scally, and  D. J. Kao, “  Molecular evidence regarding the origin of echolocation and flight in bats,”  Nature 403,  188 – 192 ( 2000 ).

10. N. B. Simmons,  K. L. Seymour, and  J. Habersetzer, “  Primitive Early Eocene bat from Wyoming and the evolution of flight and echolocation,”  Nature 451,  818 – 821 ( 2008 ).

11. S. Haykin,  Y. B. Xue, and  P. Setoodeh, “  Cognitive radar: Step toward bridging the gap between neuroscience and engineering,”  Proc. IEEE 100,  3102 – 3130 ( 2012 ).

12. M. Vespe,  G. Jones, and  C. J. Baker, “  Lessons for radar: Waveform diversity in echolocating mammals,”  IEEE Signal Process. Mag. 26,  65 – 75 ( 2009 ).

13. S. D. Gordon and  H. M. Hofstede, “  The influence of bat echolocation call duration and timing on auditory encoding of predator distance in noctuoid moths,”  J. Exp. Biol. 221,  jeb171561 ( 2018 ).

14. M. Smotherman,  M. Knörnschild,  G. Smarsh, and  K. Bohn, “  The origins and diversity of bat songs,”  J. Comp. Physiol. A 202,  535 – 554 ( 2016 ).

15. Z. Fu,  N. Xu,  G. Zhang,  D. Zhou,  L. Liu,  J. Tang,  P. H.-S. Jen, and  Q. Chen, “  Evoked potential study of the inferior collicular response to constant frequency-frequency modulation (CF-FM) sounds in FM and CF-FM bats,”  J. Comp. Physiol. A 205,  239 – 252 ( 2019 ).

16. R. A. Altes and  E. L. Titlebaum, “  Bat signals as optimally Doppler tolerant waveforms,”  J. Acoust. Soc. Am. 48,  1014 – 1020 ( 1970 ).

17. J. J. Kroszczynski, “  Pulse compression by means of linear-period modulation,”  Proc. IEEE. 57,  1260 – 1266 ( 1969 ).

18. R. Brabant,  Y. Laurent,  U. Dolap,  S. Degraer, and  B. Poerink, “  Comparing the results of four widely used automated bat identification software programs to identify nine bat species in coastal Western Europe,”  Belg. J. Zool. 148,  119 – 128 ( 2018 ).

19. S. Haykin, “  Cognitive radar: A way of the future,”  IEEE Signal Process. Mag. 23,  30 – 40 ( 2006 ).

20. X. L. Sheng,  C. P. Dong, and  L. X. Guo, “  A bioinspired twin inverted multiscale matched filtering method for detecting an underwater moving target in a reverberant environment,”  Sensors 19,  5305 ( 2019 ).

21. I. Djurović and  A. Wojciechowski, “  Quasi-maximum likelihood-based estimator of the hyperbolic frequency modulated signals,”  Digit, Signal Process. 142,  104194 ( 2023 ).

22. I. Djurović, “  Random sample consensus algorithm for the hyperbolic frequency modulated signals parameters estimation,”  Signal Process. 218,  109390 ( 2024 ).

23. X. D. Jiang and  S. L. Wu, “  A novel parameter estimation for hyperbolic frequency modulated signals using group delay,”  Digit, Signal Process. 116,  103114 ( 2021 ).

24. S. Yao,  Y. Zhang,  Y. Xu,  Y. Gu,  Q. Wu, and  X. Liu, “  An improved parameter estimation of HFM signals based on IRLS linear fitting of extracted group delay,”  Signal Process. 217,  109347 ( 2024 ).

25. J. Dicecco,  J. E. Gaudette, and  J. A. Simmons, “  Multi-component separation and analysis of bat echolocation calls,”  J. Acoust. Soc. Am. 133,  538 – 546 ( 2013 ).

26. J. Marsal,  M. Rudnicki,  A. Jedel,  R. Salamon, and  I. Kochanska, “  Mutual clutter suppression techniques for FM sonars,”  Arch. Acoust. 41,  721 – 729 ( 2016 ).

27. C. Xue,  Y. M. Gu, and  Z. X. Gong, “  Direction of arrival estimation of wideband hyperbolic frequency modulation signals using parameterized time-frequency analysis,”  Acta Acust. 48,  27 – 40 ( 2023 ).

28. S. Parsons,  C. W. Thorpe, and  S. M. Dawson, “  Echolocation calls of the long-tailed bat: A quantitative analysis of types of calls,”  J. Mammal. 78,  964 – 976 ( 1997 ).

29. W. M. Masters and  S. C. Jacobs, “  The structure of echolocation sounds used by the big brown bat Eptesicus fuscus: Some consequences for echo processing,”  J. Acoust. Soc Am. 89,  1402 – 1413 ( 1991 ). 

30. D. A. Abraham,  Underwater Acoustic Signal Processing: Modeling, Detection, and Estimation, 1st ed. (  ASA Press,  Ellicott City, MD,  2019 ), pp.  48 – 51 . 

31. L. Cohen, “  The scale representation,”  IEEE Trans. Signal Process. 41,  3275 – 3292 ( 1993 ). 

32. Q. W. Xu,  H. F. Kuang,  L. Kneip, and  S. Schwertfeger, “  Rethinking the Fourier-Mellin transform: Multiple depths in the camera's view,”  Remote Sens. 13,  1 – 10 ( 2021 ). 

33. J. W. Yang,  Z. D. Lu,  Y. Y. Tang,  Z. Yuan, and  Y. J. Chen, “  Quasi Fourier-Mellin transform for affine invariant features,”  IEEE Trans. Image Process. 29,  4114 – 4129 ( 2020 ). 

34. A. O. Mac,  R. Gibb, and  K. E. Barlow, “  Bat detective-deep learning tools for bat acoustic signal detection,”  PLoS Comput. Biol. 14,  e1005995 ( 2018 ). 

35. A. De Sena and  D. Rocchesso, “  A fast Mellin and scale transform,”  EURASIP J. Adv. Signal Process. 2007,  1 – 9 . 

36. H. Sundaram,  S. D. Joshi, and  R. K. P. Bhatt, “  Scale periodicity and its sampling theorem,”  IEEE Trans. Signal Process. 45,  1862 – 1865 ( 1997 ). 

37. B. Ristic and  B. Boashash, “  Scale domain analysis of a bat sonar signal,” in  Proceedings of IEEE-SP International Symposium on Time-Frequency and Time-Scale Analysis, Philadelphia, PA ( 1994 ), pp.  373 – 376 . 

38. G. Yu, “  A multisynchrosqueezing-based high-resolution time-frequency analysis tool for the analysis of non-stationary signals,”  J. Sound Vib. 492,  115813 ( 2021 ). 

39. X. F. Song,  P. Willett, and  S. L. Zhou, “  Range bias modeling for hyperbolic-frequency modulated waveforms in target tracking,”  IEEE J. Ocean Eng. 37,  670 – 679 ( 2012 ). 

40. M. Park and  R. Allen, “  Pattern-matching analysis of fine echo delays by the spectrogram correlation and transformation receiver,”  J. Acoust. Soc Am. 128,  1490 – 1500 ( 2010 ). 

41. M. V. Reyes Reyes,  S. Baumann-Pickering,  A. Simonis,  M. L. Melcón,  J. Trickey,  J. Hildebrand, and  M. Iñíguez, “  High-frequency modulated signals recorded off the Antarctic peninsula area: Are killer whales emitting them?,”  Acoust. Aust. 45,  253 – 260 ( 2017 ). 

© 2024 Acoustical Society of America.   

 

PHS: A Pulse Sequence Method Based on Hyperbolic Frequency Modulation for Speed Measurement

Tao Ping

onlinelibrary.wiley.com

---

1. Introduction

The channel in the marine environment is a time-varying and space-varying channel [1]. The fading effect of the time-varying channel is divided into two situations:

• (1)  The frequency-domain fading effect caused by the frequency-varying characteristics of the channel, such as frequency dispersion and multipath
• (2)  Time-domain fading characteristics due to the time-varying characteristics of the channel, such as fluctuation and movement

In general, the so-called fading refers to the frequency-domain fading, and the time-domain fading generally refers to Doppler fluctuation. The unstable effect of pulse-truncated continuous wave (PCW) signal in the channel limits the effectiveness of speed measurement. Due to the Doppler invariant effect of HFM signal [2], in the underwater acoustic detection, the HFM signal is the most preferred [2–4]. However, some frequency bands have too much transmission loss in the channel, and a single HFM signal may not be able to detect the target.

In order to overcome the above limitations of speed measurement and ranging, a pulse sequence method based on HFM for speed measurement (PHS) is proposed, which uses HFM signals of different frequency bands and pulse widths in the sequence. Therefore, PHS method can not only measure the speed but also improve the accuracy of speed measurement and distance measurement. The main contributions of this paper are threefold:

• (1)  The PHS method employs HFM signals of different frequency bands and pulse widths in the sequence. And then, there are some problems under marine environments; for example, due to excessive propagation loss in certain frequency bands, the echo energy is insufficient and cannot effectively detect the target, which can be thus avoided
• (2)  Different combinations of HFM signals in the sequence can be coherent accumulation, and the signal-to-noise ratio (SNR) of the signals is improved. Therefore, the signals are more obvious
• (3)  The HFM signals in the sequence can mutually calculate the speed and distance of the target, reducing the calculation error caused by a single signal calculation, and the accuracy of velocity measurement and ranging is thus greatly improved

In Peng et al. [5], a joint linear frequency modulation and hyperbolic frequency modulation approach for speed measurement (JLHS) is proposed. The JLHS method uses the same pulse width and frequency band of positive and negative frequency modulation signals (LFM+HFM) for speed measurement and ranging. On the other hand, two signal modulation methods are required to be opposite in JLHS. Compared with JLHS, in the PHS method, the HFM signals are only not to be completely consistent, which relaxes the requirements of bandwidth and pulse width and makes it more suitable for general conditions. On the other hand, since the tolerance of LFM to moving targets is far less than that of HFM, when the target speed is too high, LFM will have no peak output after matched filtering, and thus, JLHS cannot realize ranging and speed measurement.

In our previous work [6], a speed measurement method of combined HFM signals (SCH) is proposed, which employs positive and negative HFM signals for speed measurement and ranging. It is well known that the channel in the marine environment is a time-varying and space-varying channel. Due to the filtering effect of the marine environment, the HFM signal of a single frequency band may cause excessive propagation loss, and the echo energy may be too weak to detect the target. Compared with SCH, in the PHS method, the HFM signals in pulse sequence adopt different frequency bands, and the more pulse forms in the pulse sequence, the easier it is for more echoes to return. Therefore, HFM pulse sequence signals are more conducive to engineering use.

2. Related Works

A new polyphase pulse compression code is proposed by Yang and Sarkar [7], which is derived from the stepwise approximation of the phase curve of a hyperbolic FM-chirp signal. And they solve the problem of relatively high sidelobe levels without Doppler effect by employing appropriate window functions. In multiuser communication systems (e.g., such as multiuser radar and sonar and multiple-access spread-spectrum communication systems), there has always been a problem, that is, the problem of frequency-hopping codes, which was successfully solved by Maric and Titlebaum [8]. The construction of a new family of frequency-hopping codes is given, and it is shown that hyperbolic frequency-hopping codes have almost ideal properties and can be used in two types of systems. To address the problem of conveniently handling the received energy while transmitting and receiving modulated energy, Whyland ([9]) proposed the use of Doppler-insensitive waveforms to modulate energy pulses or subpulses to probe a defined environment. For the sonar velocity measurement problem, many scholars are currently conducting research. Shao et al. [10] proposed the use of HFM+PCW-combined signal at the Western Acoustics Conference. The HFM signal is used for ranging, and the PCW is used for velocity measurement. The PCW signal cannot consistently and effectively contact the target due to its unstable operation in the sound field. Therefore, PCW can achieve speed measurement in echoes with high SNR. When the SNR does not meet the requirements slightly, PCW will cause a large speed measurement error. Peng et al. [5] used HFM and LFM signals with the same frequency band and the same pulse width for speed measurement. This method takes advantage of the advantages of HFM and LFM at the same time, but it needs to meet certain requirements for SNR. When the SNR is too low, LFM has no peak output, resulting in failure of distance and speed calculation. HFM waveform has inherent Doppler invariant characteristics. Based on this, Meng et al. [4] worked out the constraints on HFM parameters in order to better reduce the multiple-access interference at the transmission end. The multipath and scaled underwater channel effects are reduced due to additional limitations on the frequency modulation rate. After extensive experimental comparisons of the proposed signaling scheme with HFM-based CDMA schemes, the improved performance of the new scheme is demonstrated. In Gini and Giannakis [11], the parameter estimation problem of the combination of polynomial phase signal and HFM is well solved. In Xin [12], an improved preamble waveform UMD-HFM is proposed. On the basis of the UD-HFM signal, a blank interval is added to resist the delay expansion and Doppler delay of the multipath channel to avoid waveform stacking shown, but the use and variation of blanking intervals are not indicated. In order to overcome the multipath effect and the strong Doppler effect of the shallow sea, the HFM-SS spread-spectrum modulation is used for communication [13], and the Doppler invariance of HFM is fully utilized. However, this paper only considers a single HFM and does not consider using the relationship between the HFMs in spread-spectrum modulation to solve the Doppler. During the communication process, UD-HFM uses the positive and negative HFM as the preamble signal to estimate the Doppler velocity [14]. In order to avoid waveform superposition, the mute time is increased. This method defaults to the invariance of the mute time in the process of calculating the Doppler factor, but the mute time is changed at this time. On the other hand, the UD-HFM signal in this paper requires that the two HFMs are signals of the same frequency band and the same pulse width, which is a waste of frequency band utilization. At the same time, it is not conducive to overcoming the frequency selection characteristics of ocean channels. Liu et al. [15] presented mathematical formulations for multipath propagation model and the corrupted echoes. The impact of the multipath propagation on target detection is then analyzed. In addition, in order to remove the ghost targets, a simple but effective algorithm is proposed. Numerical simulation results show the satisfactory performance. In Murray [16], an extended matching filter is introduced into the HFM waveform in active sonar systems and provides an accurate closed-form solution to Doppler bias in arrival time estimates. The solution is suitable for broadband and narrowband HFM signals.

3. Ranging and Speed Measurement Based on PHS Method

According to the properties of the Fourier transform, the convolution of two signals in the time domain is equivalent to the multiplication of their FFT in the frequency domain. Convolution in the time domain can also realize the velocity measurement function. However, the convolution calculation in the time domain is more complex. This is because the convolution calculation in the time domain requires the signal to multiply and add different shift points, which requires a large amount of computation and more hardware memory, while the FFT multiplication in the frequency domain is simple to calculate and easier to implement. Therefore, in this paper, we use HFM signals of different frequency bands and pulse widths in the sequence to realize speed measurement.

Figure 1 shows the working process of the PHS method. When active sonar works, the transmitting system transmits several acoustic signals with specific information into the seawater separately, such as HFM signal 1 and HFM signal 2, which are called the transmitting signals. When the transmitting signals travel in seawater and meet targets, the echo signals will be generated. The echo signals propagate in the sea water according to the law of propagation and reach the hydrophone, which convert the acoustic signals into electrical signals. The electrical signals are processed by the signals (matching filtering and obtaining the peak time of each HFM signal, designing the function model and calculating, and coherent integration MTD operating between pulse trains) to obtain the distance and speed of the target.

The work processing of the PHS method.

4. The Principle of Velocity Measurement by Pulse Sequence Signals

Let T denote the pulse width of the HFM signal, f₀ denote the starting frequency of the HFM signal, f₁ denote the ending frequency of the HFM signal, and s_s(t) denote the HFM transmitting signal changing over time. Then, s_s(t) can be calculated by

(1)

where t^′ = (T/2) × ((f₁ + f₀)/(f₁ − f₀)) and k = (Tf₀f₁)/(f₁ − f₀).

Let f_s(t) denote the instantaneous frequency of HFM transmitting signal, and it can be expressed as the derivative of the signal phase with respect to time divided by 2π. We have [6]

(2)

The velocity of the target is denoted by v. When the target is moving at a speed of v, the relative motion between the sonar and the target results in a pulse width of T for the transmitted signal. At the receiving point, the transmitted signal becomes a signal with pulse width of T/η. Therefore, the pulse width of the echo is linearly compressed or stretched η times. And we have [6]

(3)

where c represents the speed of sound in water and c = 1500 m/s.

Let s_r(t) represent the received echo signal. Due to the radial movement between the target and the sonar platform, s_r(t) can be calculated as

(4)

Let f_r(t) represent the instantaneous frequency of the received echo. According to Equation (4), f_r(t) can be expressed as

(5)

Since the HFM signal is insensitive to Doppler, the HFM signal has the characteristic of Doppler invariance [2]. Moreover, the change rule of the instantaneous frequency of the received signal remains unchanged, except that the instantaneous frequency f_s(t) of the original signal is shifted by a time t₀, where t₀ represents matched filter delay caused by target Doppler. We have [6]

(6)

Based on Equation (2), Equation (5), and Equation (6), t₀ can be computed as

(7)

In practical applications, the arrival time of the target is unknown, and the Doppler-induced delay t₀ and the uncertainty of the arrival time of the target coexist, resulting in a single HFM signal unable to obtain a resolvable Doppler-induced delay t₀, as shown in Figure 2.

The delay after matched filtering caused by velocity.

Frequency band and pulse width are the two key elements to consider when HFM signals are used for object detection. In order to obtain the delay difference and delay ratio after matched filtering, two HFM pulse signals (HFM pulse signal 1 and HFM pulse signal 2) in the pulse sequence are adopted.

Note: in this paper, HFM signal represents HFM pulse signal.

HFM signal 1: the starting frequency is denoted by f₁₀, the ending frequency is denoted by f₁₁, and the pulse width is denoted by T₁.

HFM signal 2: the starting frequency is denoted by f₂₀, the ending frequency is denoted by f₂₁, and the pulse width is denoted by T₂.

For a moving target, the time delay t_d1 of HFM signal 1 can be computed as Equation (8). On the other hand, the time delay t_d2 of HFM signal 2 can be computed as Equation (9).

(8)

(9)

where

(10)

Dividing Equation (8) by Equation (9), we can obtain the ratio as follows:

(11)

Now, let us derive the formulas of both ranging and speed measurement. Assume that the velocity v of the target towards the sonar system is positive. Two combined HFM signals in pulse sequence, HFM signal 1 and HFM signal 2, are transmitted. Let t₁ and t₂ represent the time of maximum matched filter of HFM signal 1 and the time of maximum matched filter of HFM signal 2, respectively. We have

(12)

(13)

According to the above two equations (Equations (12) and (13)), the distance R between the sonar and the target can be computed as

(14)

Another form of R is

(15)

where arrival time of the pulse is denoted by τ.

According to Equations (14) and (15), τ is obtained.

(16)

And then, based on Equation (12) and Equation (16), t_d1 can be computed by

(17)

According to Equations (3), (16), and (17), the target speed v can be obtained.

(18)

where

(19)

The ideal transmission channel is an infinite space composed of lossless and uniform medium, and during the propagation process, the signal cannot have any distortion. However, it is well known that the seawater medium space is a lossy heterogeneous medium space. In addition to general absorption and diffusion, the signal in sea water is also affected by multipath effect, channel time-varying and fluctuation effect, which result in the broadening of the echo and the difficulty in distinguishing the echo position of the combined echo signal. In order to achieve accurate speed measurement, we employ multiple HFM signals in pulse sequence, and the HFM signals adopt different frequency bands, and the more pulse forms in the pulse sequence, the easier it is for more echoes to return. Therefore, the signals are more obvious. Based on the above analysis, we can see that the HFM pulse sequence signals are more conducive to engineering use.

5. Moving Target Detection (MTD) between Pulse Sequences

The moving target detection (MTD) processing in pulse sequence is shown in Figure 3. It is assumed that the number of peak output of different HFM signals in the pulse sequence is N. Using the N peak outputs of pulse sequence to perform calculation in pairs, the speed and the corresponding distance can be obtained. Therefore, the total number of speeds and corresponding distances of the target is . However, since the ocean environment changes in time and space, the ocean channel is equivalent to a filter. The signal in some frequency bands has too much propagation loss, resulting in too low signal energy in the echo that cannot be effectively detected. On the other hand, although some echoes can be detected, the SNR is too low, and the noise leads to an error between the arrival time of the signal and the actual arrival time of the echo of the target. Therefore, the peak outputs with high SNR are selected in the pulse sequence to calculate the speed and distance, which will make the calculation results more accurate.

Signal processing diagram of pulse sequences.

6. Processing between Pulse Sequences

6.1. Incoherent Integration

Modelling the received echo sequence, that is, removing the phase information, for cross-period addition is called noncoherent integration or integration after detection. Generally speaking, since noncoherent integration does not utilize phase information, its detection performance is inferior to that of coherent integration. The difference between coherent integration and noncoherent integration is called detection loss. The detection loss is related to the SNR of the input. The larger the SNR is, the smaller the detection loss is. To take an extreme example, when the SNR is infinite (i.e., the noise is zero), the result of noncoherent integration is the same as that of coherent integration, and then, the detection loss is zero. In fact, as long as the input SNR is greater than 1, the detection loss is relatively small, and then, the coherent integration can be replaced by noncoherent integration. On the one hand, noncoherent integration is relatively simple to implement in engineering, and there is no strict coherence requirement for the system. On the other hand, for most moving targets, the fluctuation of the echo signals will obviously destroy the phase coherence of the adjacent echo signals. Therefore, even if the radar system has good coherence, it is difficult to obtain ideal coherent integration for undulating echoes. Therefore, although the SNR of noncoherent integration is not as good as coherent integration, noncoherent integration is often used in many cases [17]. However, noncoherent integration does not make full use of the phase of the signal, and then, the gain ratio is smaller than that of coherent integration.

6.2. Coherent Integration

Using the velocity and the corresponding distance, the echo signals are transplanted to the same starting point to carry out coherent integration MTD operation. And the coherent integration MTD is an integration method to improve the SNR of the target, which is generally performed on the complex envelope of the intermediate frequency signal or the zero intermediate frequency signal. Moreover, the coherent integration MTD retains the phase relationship between the received pulses and can increase the accumulated signal energy. That is, coherent integration utilizes the phase information of all the pulses. It is assumed that the total number of pulse echoes received during a pulse accumulation period is N, and each pulse cycle is divided into M distance gates. Discrete sampling is carried out for N pulse echoes, respectively, and let x_nm represent the sampling data on the mth distance gate of the nth pulse echo. Then, the sampling data of N pulse echo sequences can be expressed as a data of N∗M dimension, as shown in Figure 4. The signal amplitude can be greatly increased by the following: (1) M distance gates are fast time steps, and pulse compression processing is carried out. (2) N pulse echoes are slow time steps, and coherent pulse integration MTD is performed. The distance and velocity obtained in Section 4 are used to remove the signal delay in the pulse sequences, which is caused by the Doppler movement of the target. After the echo signals are rearranged, MTD operation is carried out, and then, a signal gain of N times can be achieved.

Diagram of coherent integration.

The time complexity of the proposed PHS method will be given by the following analysis. It is assumed that the number of the HFM signals in the pulse sequences is N. Since echo signal in each pulse sequence needs to be matched and filtered separately, the time complexity is O(N). On the other hand, during space beamforming, due to different frequency bands in the sequences, separate beamforming is required, so the space complexity is O(N). When the signal frequency bands in the sequences are the same and the pulse widths are different, the beamforming can only be done once, and the spatial complexity is thus O(1).

7. Simulation and Results

7.1. Simulation Settings

Three simulated environments were used for the performance analysis. In the following simulated environments, the distance between the sound source and the target is 7.5 km, the speed of the target is 14 m/s, the SNR = −10 dB, and the sample frequency f_sa = 7000 Hz. Here, the frequency band is denoted by F_s, and the pulse width is denoted by T_s.

Simulated environment 1: the HFM pulse sequences consist of the following HFM signals: for HFM signal 1, F_s is 200 Hz-1000 Hz, and the pulse width is 1 s. For HFM signal 2, F_s is 300 Hz-1200 Hz, and T_s is 2 s. For HFM signal 3, F_s is 400 Hz-1400 Hz, and T_s is 3 s. For HFM signal 4, F_s is 500 Hz-1600 Hz, and T_s is 4 s. For HFM signal 5, F_s is 600 Hz-1900 Hz, and T_s is 6 s.

Simulated environment 2: the HFM pulse sequences consist of the following HFM signals: for HFM signal 1, F_s is 100 Hz-200 Hz, and T_s is 1 s. For HFM signal 2, F_s is 700 Hz-900 Hz, and T_s is 2 s. For HFM signal 3, F_s is 1000 Hz-1200 Hz, and T_s is 3 s. For HFM signal 4, F_s is 1700 Hz-1900 Hz, and T_s is 4 s.

Simulated environment 3: the HFM pulse sequences consist of the following HFM signals: for HFM signal 1, F_s is 100 Hz-200 Hz, and T_s is 2 s. For HFM signal 2, F_s is 1000 Hz-700 Hz, and T_s is 3 s. For HFM signal 3, F_s is 1000 Hz-1300 Hz, and T_s is 3 s. For HFM signal 4, F_s is 1100 Hz-1300 Hz, and T_s is 1 s.

7.2. Simulation Results

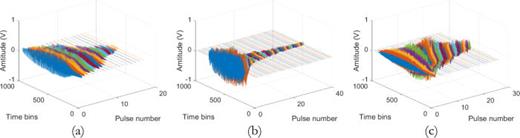
For simulated environment 1, the performance analysis is shown in Figures 5 and 6. The numerical results of PHS are given in Table 1. From Figure 5, it can be seen that, after matched filtering, the signal echo time of HFM signal 1, HFM signal 2,HFM signal 3, HFM signal 4, and HFM signal 5 is 10.0236 s, 10.0502 s, 10.0792 s, 10.1096 s, and 10.1652 s, respectively. Figure 6 shows the MTD operation based on pulse sequence method. According to Equation (18), the value of v is 13.9914 m/s. It can be seen from Table 1 that the speed measurement error and the ranging error of PHS are 0.061429% and 0%, respectively. The ranging error of HFM signal 1, HFM signal 2, HFM signal 3, HFM signal 4, and HFM signal 5 is 0.0236%, 0.502%, 0.792%, 1.096%, and 1.652%, respectively. Compared with HFM signal 1, HFM signal 2, HFM signal 3, HFM signal 4, and HFM signal 5, the ranging measurement accuracy of PHS is all improved by 100%.

Single HFM signal detection under simulation environment 1.

Pulse sequence method based on HFM signal under simulation environment 1.

Table 1. For simulated environment 1: comparison of simulation results.

Echo time of single signal (s)					Ranging of single signal (km)					Ranging of PHS (km)	Speed of PHS (m/s)
HFM signal 1	HFM signal 2	HFM signal 3	HFM signal 4	HFM signal 5	HFM signal 1	HFM signal 2	HFM signal 3	HFM signal 4	HFM signal 5
10.0236	10.0502	10.0792	10.1096	10.1652	7.5177	7.53765	7.5594	7.5822	7.6239	7.5	13.9914

Ranging error of PHS	Speed measurement error of PHS	Ranging error of single signal					Range accuracy improvement ratio compared to
		HFM signal 1	HFM signal 2	HFM signal 3	HFM signal 4	HFM signal 5	HFM signal 1	HFM signal 2	HFM signal 3	HFM signal 4	HFM signal 5
0%	0.061429%	0.236%	0.502%	0.792%	1.096%	1.652%	100%	100%	100%	100%	100%

For simulated environment 2, the performance analysis is shown in Figures 7 and 8. The numerical results of PHS are given in Table 2. From Figure 7, it can be seen that, after matched filtering, the signal echo time of HFM signal 1, HFM signal 2, HFM signal 3, and HFM signal 4 is 10.0376 s, 10.1696 s, 10.3392 s, and 10.7160 s, respectively. Figure 8 shows the pulse sequence method based on HFM signals. According to Equation (18), the value of v is 14.0019 m/s. It can be seen from Table 2 that the speed measurement error and the ranging error of PHS are 0.013571429% and 0%, respectively. The ranging error of HFM signal 1, HFM signal 2, HFM signal 3, and HFM signal 4 is 0.376%, 1.696%, 3.392%, and 7.16%, respectively. Compared with HFM signal 1, HFM signal 2, HFM signal 3, and HFM signal 4, the ranging measurement accuracy of PHS is all improved by 100%.

Single HFM signal detection under simulation environment 2.

Pulse sequence method based on HFM signal under simulation environment 2.

Table 2. For simulated environment 2: comparison of simulation results.

Echo time of single signal (s)				Ranging of single signal (km)				Ranging of PHS (km)	Speed of PHS (m/s)
HFM signal 1	HFM signal 2	HFM signal 3	HFM signal 4	HFM signal 1	HFM signal 2	HFM signal 3	HFM signal 4
10.0376	10.1696	10.3392	10.7160	7.5282	7.6272	7.7544	8.037	7.5	14.0019

Ranging error of PHS	Speed measurement error of PHS	Ranging error of single signal				Range accuracy improvement ratio compared to
		HFM signal 1	HFM signal 2	HFM signal 3	HFM signal 4	HFM signal 1	HFM signal 2	HFM signal 3	HFM signal 4
0%	0.013571429%	0.376%	1.696%	3.392%	7.16%	100%	100%	100%	100%

For simulated environment 3, the performance analysis is shown in Figures 9 and 10. The numerical results of PHS are given in Table 3. From Figure 9, it can be seen that, after matched filtering, the signal echo time of HFM signal 1, HFM signal 2,HFM signal 3, and HFM signal 4 is 10.0754 s, 9.8682 s, 10.245 s, and 10.1224 s, respectively. Figure 10 shows the pulse sequence method based on HFM signals. According to Equation (18), the value of v is 13.996 m/s. It can be seen from Table 3 that the speed measurement error and the ranging error of SPHS are 0.02857% and 0%, respectively. The ranging error of HFM signal 1, HFM signal 2, HFM signal 3, and HFM signal 4 is 0.754%, 1.318%, 2.45% and 1.224%, respectively. Compared with HFM signal 1, HFM signal 2, HFM signal 3, and HFM signal 4, the ranging measurement accuracy of PHS is all improved by 100%.

Single HFM signal detection under simulation environment 3.

Pulse sequence method based on HFM signal under simulation environment 3.

Table 3. For simulated environment 3: comparison of simulation results.

Echo time of single signal (s)				Ranging of single signal (km)				Ranging of PHS (km)	Speed of PHS (m/s)
HFM signal 1	HFM signal 2	HFM signal 3	HFM signal 4	HFM signal 1	HFM signal 2	HFM signal 3	HFM signal 4
10.0754	9.8682	10.245	10.1224	7.55655	7.40115	7.68375	7.5918	7.5	13.996

Ranging error of PHS	Speed measurement error of PHS	Ranging error of single signal				Range accuracy improvement ratio compared to
		HFM signal 1	HFM signal 2	HFM signal 3	HFM signal 4	HFM signal 1	HFM signal 2	HFM signal 3	HFM signal 4
0%	0.02857%	0.754%	1.318%	2.45%	1.224%	100%	100%	100%	100%

8. Conclusion

The fuzzy function of HFM signal has the shape of the blade, which makes the velocity and distance to be coupled together. Due to the Doppler frequency shift caused by the target movement, the peak value after the matched filtering has a time delay in the time domain, resulting in the failure of a single HFM to accurately range. In this paper, based on the time delay of signals with different frequency bands or different pulse widths, a pulse sequence method based on HFM for speed measurement (PHS) is proposed, which uses HFM signals of different frequency bands and pulse widths in the sequence. The proposed method can not only guarantee the speed measurement but also improve the accuracy of the speed measurement and distance measurement.

In future research, we will realize simulation in more complex scenarios, such as multitarget speed measurement and simulation in the presence of clutter.

Conflicts of Interest

The authors declare that they have no conflicts of interest.

Acknowledgments

This work was supported in part by the Shandong Smart Ocean Ranch Engineering Technology Collaborative Innovation Center, in part by the Shandong Agricultural Science and Technology Service Project (No. 2019FW037-4), in part by the research fund for high-level talents of Qingdao Agricultural University (No. 6631119041), and in part by the Shandong Technology Innovation Guidance Program (No. 2020LYXZ023).