Making the Panama Canal Closed Cycle
The Panama Canal has operated open loop since its inception, depending on controlling water flow from Gatun Lake down to sea level to lift ships up to Gatun level via stair step locks, and then lower them down to sea level on the opposite coast. This releases a lock chamber full of fresh water into the sea each time. This process is dependent on solar evaporation-rain cycle to lift and freshen sea water back up to the lake. Lately, with climate change and El Nino, this has become problematic. By capturing the incremental energy released during each lock step from water flow, the energy with addition from PV solar could be used to pump water from a reservoir at sea level at each end of the canal back up to lake level, so there would be minimum loss of water, making the canal closed cycle. This is a variant of closed cycle gravity energy storage. The articles below summarize the problem and solution components technology.
Panama Canal Implements New Water-Saving Measures Amidst Low Rainfall
In 2019, the Panama Canal faced its fifth driest year in 70 years due to changing rainfall patterns, resulting in historic low water levels at Katyn Lake. Rainfall was 20% below the historical average, following several years of lower than average rainfall. Moreover, water evaporation levels rose by 10% due to a 0.5 to 1.5 degree Celsius temperature increase.
The Panama Canal has responded by announcing new measures, effective from February 15th, to maintain operational water levels and ensure reliability for customers. These measures include freshwater surcharge adjustments, changes to the booking system, and transit itinerary creation. This proactive approach follows the successful implementation of water-saving techniques, such as the cross-filling locks method, which saves water equivalent to that used in 60,000 gallons daily.
Other ongoing water-saving measures include suspending power generation at the Gatton hydraulic plant, eliminating hydraulic assistance at the Panamax locks, and employing water-saving basins at the Neo Panamax lock. The Panama Canal remains committed to water conservation and expanding its investment program to address the sustainability of the water supply.
The Panama Canal Adapts: Strategic Measures for Water Savings - Autoridad del Canal de Panamá
It is not an exclusive concern of the Panama Canal or the country; it is a global problem that affects humanity. The year 2023 records historically high temperatures in the Atlantic Ocean, exacerbated by the presence of the El Niño phenomenon, which raises the temperature of the Pacific Ocean and, in the case of Panama, delayed the start of the rainy season, resulting in a significant decrease in the levels of freshwater in the reservoirs of the Panama Canal, essential for its operation.

Resource Optimization
To address these challenges, the Canal has taken water-saving measures to supply 55% of the population and provide competitive and continuous service to global maritime trade.
One of the implemented measures is cross-filling in the Panamax locks. This maneuver involves reusing water from one lock chamber for use in the other, saving the equivalent of the average consumption of five daily transits.
Additionally, to the extent that the size of the vessels allows, simultaneous lockages are performed, with two ships transiting at the same time, occupying the same chamber.
Furthermore, the transit schedule has been optimized to maximize water savings in each chamber and accommodate the highest number of vessels. In the neopanamax locks, the direction and scheduling of transits are analyzed to make the most of every drop of this resource.
Since 2020, the Canal has been working on the Water Program. This initiative seeks to provide a comprehensive response to the water challenge, with a focus on ensuring this vital resource for the next 50 years.
Other Measures
As announced two weeks ago, starting November 1st, the average transits through the Canal will be adjusted to 31 vessels per day: nine through the neopanamax locks and 22 through the panamax locks. Customers are recommended to make reservations, when possible, to secure their transit through the route.
The Panama Canal announces any measures that may affect customers well in advance, before the furthest vessel departs. Additionally, the maritime route provides real-time information for customers to make their business decisions, through the links also maintained at the bottom of this note.
The Panama Canal fulfills its constitutional responsibility to manage freshwater resources for human consumption and provide efficient service to global maritime trade through a transparent and sustainable approach.
Links:
Vessels in queue for transit
Real-time Weather Radar Animation (updated every 5 minutes)
Daily average level of Alhajuela reservoir for the last 12 months
Daily average level of Gatun Reservoir for the last 12 months
Daily precipitation (rainfall) by sub-basins (Alhajuela/Gatun) and cumulative in CHCP current year 2023
About the Panama Canal Authority (ACP)
The Panama Canal Authority (ACP) is an autonomous legal entity of the Republic of Panama in charge of the operation, administration, management, preservation, maintenance, and modernization of the Panama Canal, as well as its activities and related services, so that the Canal may operate in a safe, continuous, efficient manner. For more information, please refer to the ACP’s website: https://www.pancanal.com or follow us on Twitter @thepanamacanal.
Gatun Lake Water Level Indicators
Introduction
Waterways are the most efficient means for transportation and the only land infrastructure with the free capacity not subject to congestion problems. Navigation is the energy and carbon-efficient mode as a ship uses 1–2 times less fuel than a train and 3–5 times less fuel than a truck and can be economically competitive [1]. Additionally, waterways can be built with pumped storage plants together with intermittent energy sources, present themselves as an innovative opportunity to, using the own head available at facility, improve the financial return of meeting the energy demand for a solar hybrid generation system with pumped storage.
In the city of Tucuruí, Brazil, the dam of the hydropower plant on the Tocantins river creates a water height difference of 61.7 m. Two locks allow the water transport and passage of local goods in the state of Pará. The operation of these locks is under the responsibility of the National Department of Transport Infrastructure (DNIT), regardless of the adjacent hydroelectric plant.
Several studies have been conducted in regard of the environmental effects of the Tucuruí dam and its upper reservoir. Curtarelli et al. [2] investigate, by mathematical modeling, the carbon emission due to the formation of the Tucuruí reservoir. The authors demonstrate that the quantity emitted in the lake is of the order of 1.1 Tg of carbon per year, highlighting the importance of the carbon inventory in energy systems and the use of less environmental impact resources. Chen et al. [3] show the impact patterns in deforestation and forest degradation due to the construction of the aforementioned hydropower plant. The implementation of such a large infrastructure (the fifth hydropower station in the world) have affected the local biodiversity in addition to the consequences of urban development.
Today, it is important to reduce the environmental and carbon footprint of dam’s appliances as the locks of the waterways. Renewable energy sources (RESs) are now considered an important and strategic way of ensuring the sustainability of projects [4], [5] and the coupling with energy storage systems contributes in their optimal exploitation in terms of reliability [6], [7] operations [7], [8] and return of investment [9].
Further investigations on the use of RES combined with energy storage for standing alone system can be found in the literature. Ma et al. [10] study the optimization of the sizing of renewable energy system for electrification of isolated areas without access to the grid, highlighting the importance of storage for the success of the project aiming at continuity and reliability due to the intermittency of the solar source. Malheiro et al. [11] also study energy optimization and programming in stand-alone systems. Evaluating a hybrid system with solar, wind and diesel sources as a backup supply, mathematically analyzes, within a year, the hourly changes in the availability of sources and energy demand. Considering that hybrid energy systems are increasingly used in isolated or energy-deficient areas, Aziz et al. [12] demonstrate that an optimized system is more economical and reliable than a power system with a single source. Ma et al. [13] study the optimization of a hybrid solar-wind system with pumped storage to serve an isolated grid with a capacity of the order of a few hundred kW. Pali and Vadhera [14] propose a new configuration of a hybrid system with wind and hydro sources for rural and isolated areas. Connecting the wind turbines directly to the energy storage, the authors highlight the cost reduction and improvements in simplicity and reliability regardless of the wind power fluctuations. Thus, the application of hybrid systems, even considering the peculiarities of each situation, can be useful in different scenarios of energy needs [5].
Researchers put particular effort into RES solutions connected with pumped hydro energy storage (PHES), which has today the most used technology in terms of capacity worldwide. Kusakana [15] proposes an optimal energy dispatch model by using a combination of solar, wind, diesel sources and PHES in order to meet the variable demand: this modelization tackles the seasonality and the intermittency of RES, which represents a continuous challenge for energy management systems (EMS). EMS of hybrid solutions counts further complexity due to the diversity and variability of diverse sources [4], [5], [12], [13], [14], [16], [17]. Analyzing the traditional scenario of power generation, Bhattacharjee and Nayak [4] analyze the application of a solar hybrid system with pumped storage searching a viable, continuous and cost-effective solution to the problem of low water availability in power plant reservoirs, demonstrating it as a good option for restoring the reservoir's performance. Xu et al. [17] observe consistent load fluctuations due to the variability of wind and solar sources that, on a large scale, can cause stability and safety threats in the electricity network. Besides, PHES can cause instabilities due to the interaction between shaft vibration and governing strategies during the connection and disconnection of the system [17].
Morabito and Hendrick [18] study a solar, wind and PAT hybrid system connected to a smart grid in a real application. The prototype uses a speed control to guarantee the operation of the machine in the BEP according to the suitable hydrological conditions, what highlights the importance of the study in the field of hybrid systems integrated to the grid.
Another aspect of energy generation from renewable sources is the operational and storage limitations of each source. Ma and Javed [19] present an integrated design of a hybrid system with solar, wind and battery storage considering the saturation limits for each source, based on economic and technical indexes. Javed et al. [20] propose a hybrid system with stored pumping and batteries as an off-grid renewable energy system. The authors use a new operating strategy based on the maximum extraction of energy stored at the point of maximum PAT efficiency, with the battery used only to meet very low levels of load. To evaluate the performance of the system, a general indicator of storage overall performance, energy utilization ratio and storage usage factor is used. In this way, the need to know the limiting characteristics of each source proposed as a solution is highlighted.
Hybrid systems may be viable in other types of power generation. Stenzel and Linssen [21] present an application concept and a new form of pumped storage using federal waterways as a lower reservoir in Germany, identifying a potential of 400 MWh. An energy solution for the transposition system is proposed by Zhang et al. [22]. The authors present a project of potential energy exploration using the head and flow in the operations of filling and draining. The authors demonstrate viable applications that seek maximum utilization of energy availability, even in facilities or places intended for other purposes. The costs involved in the design, installation and maintenance are decisive in the adoption and determine the viability of renewable energy systems. An adequate economic approach to energy systems can be carried out considering the annual cost and the payback of the systems [23], [24] or the effective cost using the net present value method [25] including availability, efficiency, installation, operation and maintenance costs.
The varied research and applications of hybrid energy systems show the feasibility of these solutions for energy supply in isolated areas, integrated into the grid, etc. However, the implementation of RES in Locks presents an interesting gap that can be investigated, with very few studies in the literature. For the Brazilian case, there are more than 20 Locks and more than a hundred other dams [26], in which the combination of head and solar radiation is very frequent, thus allowing the use of both sources for energy generation and storage. The results of which can easily be applied to hydroelectric plants and transposition systems worldwide.
In this work, in particular, the study to demonstrate the potential of using these structures with renewable energy systems focuses on performing an analysis of energy alternatives for the operation of the Tucuruí locks considering two possible scenarios: one with pure photovoltaic energy supply and the other one with a hybrid system composed of solar and hydraulic sources, with pumped hydro energy storage. Moreover, the economic feasibility of each alternative and the payback is investigated. The evaluation of the alternatives studied shows that the hybrid system with pumped storage is more economically (around 40%) and technically feasible due, mainly, to the availability of head and the high costs of a purely photovoltaic plant.
This paper is structured as follows: in Section 2 a brief description of the site, location and main characteristics of the hydrological use is presented. Availability to use potential and solar energy is shown. Section 3 contains the work approaches regarding the proposed solutions to meet the energy demand of the facility, the systems designed, the selection of machines and the calculation of PAT performance in pump mode. The methodology for calculating energy costs and payback time for each proposal analyzed is also presented. Section 4 discusses the results of the analysis from the previous section and, finally, the conclusion is presented in Section 5.
Section snippets
Characteristics of Tucuruí locks
The Tucuruí hydroelectric plant is the fifth largest in the world and has an installed capacity of 8,535 MW, distributed in 25 hydraulic generating units with 22.5, 350 and 395 MW power capacity. The turbines take advantage of a 61.7 m net head maintained by an earth and rock dam of over 11 km. Its spillway is designed for a maximum flow of 110,000 m3/s, characterizing it as the world's largest in spillway capacity. This feature allows the possibility of exploitation of the water resource due
Demand
For the calculation of the demand profile, the following procedure was performed. The total energy consumed in the transposition operations, which includes filling and draining, and the functioning of the control system was measured directly in the energy meters of the Locks in two months. The one of greatest consumption was considered, in which the total energy for operation of the installation was 135,090 kWh. From this, the daily average of 4,503 kWh was calculated. In Eq. (1), the
Photovoltaic-only alternative
For the purely photovoltaic system, the power of 1,569 kW is obtained by the 4,757 photovoltaic modules, occupying an area of 9,249 m2. Fig. 11 shows the comparison between hourly demand and photovoltaic production. The solar energy shown was calculated according to Eq. (5). The graph, with sunshine data for the critical month (December), shows that solar production meets the demand for operation, guaranteeing in the daily balance a surplus stored in the grid of about 1,500 kWh.
Hybrid system alternative
Fig. 12 presents
Conclusions
The installed global capacity of renewable energy grows steadily every year, and more environmentally friendly and cost-effective facilities are designed according to the specificity of the site [17], [18], [20].
The project for energy solution of the Lock operations studied by Zhang et al. [22] proposes the use of a hydraulic turbine with variable rotational speed for the exploitation of the fluctuating flow rate and available head. This work, in turn, explores other designing key-factors
Declaration of Competing Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Acknowledgement
Authors wish to acknowledge the assistance from National Department of Transport Infrastructure (DNIT), Carlos Gil of Eletrobras Eletronorte for data and site visits, CNPq (Proc. n. 307241/2018-1) and PROPESP/UFPA for all support in this project. Authors also wish to thank the WBI in the frame of CAPES program and EPOC project, funded by Federal Public Service of Economy of Belgium.
Cited by (25)
Challenges and opportunities for a South America Waterway System
2022, Cleaner Engineering and Technology
It also has lower impacts on its surrounding areas, particularly when compared to roads and railways (Rohács and Simongáti, 2007). Moreover, inland water transport has been successfully implemented in Europe (Merchan et al., 2019), China (Stefaniec et al., 2020), India (Praveen and Rajakumar, 2015), Bangladesh (Awal et al., 2014), Nigeria (Chukwuma, 2014), Canada (Zheng and Kim, 2017), Brazil (Furtado et al., 2020) and has been under expansion in Myanmar (Nam and Win, 2014), among other nations. South America has one of the world's highest potentials for waterways, given its relatively flat topography and large water availability (Fig. 1).
Canal lock variable speed hydropower turbine design and control
ietresearch.onlinelibrary.wiley.com1 Introduction
In ‘Hauts de France’ region, more than 200 locks can be found all along a very dense network of rivers and canals allowing for goods and containers transportation. According to the rather flat landscape of the region, the locks are characterised by rather low water height differences between their upstream and downstream sides (generally around 3 m). Nevertheless, in a general context of energy saving, the potential energy recuperation during lock operation must be examined carefully.
A typical lock facility (Fig. 1) is characterised by a constant hydraulic head difference between upstream, H1, and downstream, H2, in the absence of any ship lock process (steady state), which is nearly independent of seasonal variations. The available gross head, ΔH(t), is quite small, in the order of few metres. When a boat arrives from the upstream direction, two identical square guillotine valves (denoted as V1 and V2 on Fig. 1), positioned on the side channels (C1 and C2), are opened simultaneously and gradually in order the lock to be filled up with water smoothly with a non-constant over time flow rate, Qi(t). By this way, it is assured that the flow of water is equally distributed in the two side channels and most important inside the lock minimum disturbances are being created on the free surface. During this operation, the gross head starts to decrease and finally the level of water becomes equal in the two sides of the top gates which then open allowing the boat to enter the lock. Finally, the lock is being drained downstream with a similar procedure, through side channels C3 and C4. If a boat comes from the downstream direction, then it is being captured inside the lock, which is being filled up until the water level reaches the upstream level.

Top (a) and side (b, c) views of the lock describing the filling (b) and draining (c) operations
The possibility of installing turbines in river locks has already been mentioned [1], but the process described is nearly impossible to be installed in an existing lock without major civil engineering modifications. However, a similar work of designing and installing a hydro-turbine in an existing lock has not come to our knowledge.
On the contrary, a lot of work has been done over the last years to develop machines capable of producing energy from low and very low head hydro resources for different applications (e.g. river dams and irrigation channels) where the head and/or flow are constant or minor changes are being observed [2, 3]. Nowadays, several types of turbines for very low head applications are available in the market [4, 5].
In conventional hydro power systems, a governor is used for controlling the turbine's speed of rotation and producing the maximum energy. In the case under consideration, the turbine will be submerged, installed inside the side flow channel of the lock, where the water current will cause the blades to rotate. However, due to the variable water level, the flow rate is never constant. Operating always at the best performance of the turbine requires the rotation speed to follow the changes of the fluid velocity. This can be achieved by adopting a variable speed control system [6]. The idea behind the variable speed operation is to adjust the rotational speed for off-designed heads and/or discharge loads, which result in a reduced efficiency and could also lead to vibrations and cavitation problems [7, 8]; thus, maximum efficiency power tracking at every operation point is being ensured [9, 10]. For an axial propeller turbine, the overall efficiency is expected to be improved [9, 11].
In addition, several studies have also focused on the design and control of systems intended for the conversion of wind or tidal energy, the principle of which is close to the problem of the conversion of canal lock hydropower into electrical energy [12-14].
The present paper is describing a project that aims in designing a hydro generator that can capture intermittent energy during the ship lock processes in the range of 30–60 kW and presenting the findings of the study. The overall goal is to develop an assembly consisting of a hydraulic machine and an energy conversion and controlling system, respecting constraints coming from the lock operation. The main characteristic of such facilities is the very low available hydraulic head, which additionally varies with time, during the operation, from its maximum value down to zero. Constraints that are being set are to minimise the effect on the operational time, minimise the intervention on the lock, and to be economically viable. One test case has been chosen as a basis for the project, but, of course, the models are not limited to that example.
In our previous works, the hydraulic machine [15] and the electrical system [16] were modelled separately and preliminary results were presented. A more detailed approach is now being followed, considering the influence of several parameters in their performance, including the interaction between the hydraulic and the electrical part of a turbine.
2 Hydraulic model of the lock
The whole system as presented in Fig. 1a is symmetrical between upstream and downstream, and between side channels. The side channels generally have a square cross-section are being made of concrete, and all are identical considering the dimensions, including the valves. Due to the symmetry, the system simulation comprises the lock, the upstream and two side channels with the corresponding valves.
It is obvious that one turbine can be installed in every side channel, but to retain the symmetry, which assures that the lock is being filled or drained as smoothly as possible, the cases of installing two or four turbines have been examined. The results presented afterwards correspond to the operation of one turbine during one lock operation (filling or draining).
2.1 Hydraulic data
The initial available gross head between the upstream level, H1, and the downstream level, H2, is ΔHG = 3.03 m and the time duration to fill or drain the lock is around to = 480 s. For one year, the total number of operations (fillings and drainages) is No = 7200. The total maximum potential theoretical energy, Eth, is
 (1)
(1)
where ρ is the water density, g the acceleration of gravity and Vlock the volume of water incorporated into the lock during one filling sequence. On an annual basis, the maximum energy corresponds to
 (2)
(2)
This hydraulic energy can be converted to electrical by two turbines installed either on the upstream side (Fig. 1) during filling the lock or on the downstream side during emptying the facility. Thus, during a full-operation cycle (fill and drain), the total theoretical available energy, and consequently the produced energy, can be doubled if four turbines are being installed.
2.2 Modelling of the lock transient operation
Due to the absence of any flow data, first a dynamic model, using Simulink®, was developed for simulating the operation of the lock without the presence of any turbine and acquiring the evolution of the flow rate and the hydraulic head. The model is taking into consideration the pressure difference between the upstream, Pup, and the lock, Plock, the overall head losses, ΔPlosses, and the inertance, ΔPinert.
 (3)
(3)
Upstream the hydraulic pressure is always constant, (4), whereas the pressure in the lock is changing over time, (5). Q is the total volume flow rate in the two side channels, whereas Qi is the flow in each side channel. The flow is being equally distributed in the two side channels. Slock is the section of the lock equal to the product of its length and width.
 (4)
(4)
 (5)
(5)
Head losses occur in the channels and the valves. For the channels, the total losses can be described by (6), where kc is the total friction coefficient in the channels and Spipe is the cross-section of the channel. The dimension of the cross-section is 2.3 × 2.3 m.
 (6)
(6)
For the valve, the model of (7) was initially applied according to [16], where hv is the opening of the valve, changing four times every 2 min in equal intervals, from zero up to the maximum opening, hv,max, and τv is an exponential time constant. The valve opening between each step is linear over a period of Δτ = 20 s.
 (7)
(7)
Finally, the pressure difference in the water that is being required to cause a change in the flow rate with time is given by (8), where Lpipe is the total length of the channels.
 (8)
(8)
The loss coefficient of the conduits can be estimated based on the head losses of the friction on the walls, the change of the direction in bends and the effects of the entrance and the exit of the channels [17]. A loss coefficient, kc = 4.087, is estimated.
The above system of equations is resolved to define the filling/draining time. The valve exponential time constant of (7) was fixed as the value for which the time is equal to to = 480 s and found to be τv = 7.17.
On Fig. 2, the evolution of the flow rate in one side channel is presented together with the available gross head and the dissipated hydraulic power, Ph. The dissipated energy, which is equal to the integration of the hydraulic power, has been also included in Fig. 2b and it can be observed that the total dissipated energy, (9), is perfectly equal to the maximum potential energy, defined before.
 (9)
(9)

Evolution of
(a) The flow rate, Qi, and gross head, ΔH, and (b) The potential hydraulic power, P, and energy, E, under the transient operation of the lock in one side flow channel with the modified valve operation and control (solid lines) and the initial law model (dash lines)
One of the main constraints, associated to the installation of the turbines, is to retain the duration of the transient operation close to the initial level (∼480 s), which will not be the case when introducing the turbines in the system. An additional source of losses will be added on the system resulting in an increase of the time cycle. The degree of the effect will depend on the selected machine and its design. A solution could be to modify the control law of the valves opening, for example, force the valve to open in one step (continuously and linearly over time) and in a time interval of τv = 60 s. The results of the modified control and operation valve law are also presented in Fig. 2. The main characteristic of the proposed solution is that the same total dissipated energy, which is again perfectly equal with the maximum potential energy, is being acquired in a shorter time interval. The maximum flow rate is higher resulting in a shorter duration of the lock process and higher maximum hydraulic power. Despite the shorter operation time, the losses in the flow channels are higher because of the higher bulk velocity (Fig. 3).

Energy in the system for the default model (blue) and modified valve law model (red)
However, attention should be given in the possibility of disturbing the free surface, especially during the filling operation of the lock, because of the sudden increase of the flow rate. By increasing the required time for the valve to be completely opened in one step, the potential effect on the boat stability can diminish, since the increment of the flow rate will be gentler and smooth, but the reduction of the total duration of the operation will not be significant.
The unsteadiness of the whole process is coming from the term of inertance, described by (8), which is not of great importance (Fig. 3). Thus, the degree of unsteadiness of the system is considerably low.
3 Hydraulic turbine design
First, a simple model of the turbine operation is being adopted and included on the dynamic model. Based on the preliminary results and by respecting specific restrictions, the hydraulic machine is being selected and designed using a more detailed approach.
3.1 Hydraulic machine pre-design
A simple model for the turbine head drop, (10), based on the overall resistance coefficient of the hydraulic machine, kt, was introduced in the dynamic model. The resistance factor (kt = 138.76 kg/m7) was defined as the value for which the time for filling the lock is equal to around 480 s. The dissipated power in the machine can be calculated by (11).
 (10)
(10)
 (11)
(11)
A part of that energy will be transformed into electricity according to the type of machines (hydraulic and electric) and associated efficiency. The level of the mechanical power can be modified by changing the imposed law of the valve, for example, decreasing the time of the valve to fully open will result in more dissipated power. However, it must always be considered the impact of the flow rate evolution, which strongly depends on the valve control law, on the stability of the free surface in the lock and therefore on the stability of the boat. The turbine head, Ht, can be calculated
 (12)
(12)
By integrating the turbine power, the total energy produced per turbine found to be Ei = 21.60 MJ, which represents 55% of the maximum potential energy. It has to be noted that this analysis proposed as a first approach is ignoring the minimum technical discharge of the turbine, which leads to a slight overestimation of the energy produced by the system. However, the total energy can be increased if the factor kt is increased, but this will affect the duration of the whole operation. Different values of the resistance coefficient correspond to different designs of the turbine. It is also expected to change the pressure drop of the machine by modifying the rotational speed of the rotor.
Therefore, the simulation model can be used as an optimisation tool for determining the correct value of kt to be used on a later step of the design procedure, for achieving the desired level of energy recuperation in compromise with the cycle duration. Fig. 4 summarises the effects on the energy recuperation and the cycle duration. By increasing the factor kt, in other words, increasing the turbine head drop, both the operation cycle and the power produced by the machine increase. The energy recuperation tends asymptotically towards to 100%, and a further increase of the factor will result in very low energy gain.

Duration of lock process (red) and energy recuperation (blue) for different values of the turbine overall resistance coefficient
3.2 Best efficiency point
From the results of the simple modelling, a first estimation of the best efficient point (BEP) or design point of the turbine can be done for any value of the loss coefficient. The BEP is determined by the optimum flow rate, turbine head and rotational speed at which the machine will have its maximum efficiency. In Fig. 5, the flow rate and head are being plotted for the case of kt = 138.76 kg/m7. The aim will be to design a machine, which will have its BEP for the maximum values of Qi and Ht. It has to be noted that the maximum value of Ht in Fig. 5 is around 1.6 m, whereas the available water level difference at the beginning of the operation is 3 m. This difference is due to the energy dissipation in the pipes and valves of the hydraulic system. At this stage of the design, the efficiency at the BEP is supposed to be ηBEP = 80%. It is expected that along the line of Fig. 5, the machine will always perform with its maximum efficiency.

Determination of the BEP
In addition, the specific diameter, Ds, and speed, Ns, can be calculated. It is obvious that these parameters are not constant during the operation of the lock, because of the variable flow rate and head. Using the following equations, and the well-known Cordier diagram [18], the speed of rotation, N, is being calculated for the BEP.
 (13)
(13)
 (14)
(14)
If the diameter of the machine is D = 2 m, slightly smaller than the width and the height of the side channels, it is found that N = 14 rpm. The calculated speed of rotation is quite small, making very difficult to design the electrical machine that will accompany the hydraulic part without gear box. A reason for that, except the very low head, can be the fact that Cordier diagram, which has been the statistical result of various commercial turbines, is not able to describe the operation of the specific application. Therefore, a higher rotational speed, at the BEP, will be assumed and fixed.
3.3 Hydraulic machine selection
The selection of the type of the hydraulic machine depends on many criteria, all of which are directly linked to the application under consideration. In the specific case, to predefine the machine type, several quantitative (available head, flow rate, rotational speed, cost) and qualitative factors (degree of intervention in the facility, portability, location) must be considered [19]. The main characteristic of the turbine under design is the very low head. It is a common practice in such applications to use axial reaction turbines and more precisely a propeller or Kaplan turbine.
As it can be understood, the design of the machine is based on two main parameters: an external diameter (in the case of an axial turbine) compatible with the cross-section dimensions of the existing channels, and the chosen value of kt. As mentioned before, the impeller speed of rotation can then be rather easily deduced using the Cordier diagram (which cannot be applied satisfactorily in the case under consideration) or a pre-defined fixed value can be used for the BEP. However, it will be clear afterwards that the final selection of the rotational speed will depend on the combination of the two systems: the hydraulic and the electrical. If the law used to model the turbine is validated, it can be observed that the use of an adequate variation of the speed of rotation during the transient process can lead to correct machine efficiency during the whole operation. Controlling, thus, the speed with the electrical machine will result in controlling the flow evolution on the system.
Additionally, the specific machine is being required to be installed with the minimum intervention on the facility, meaning no civil works must be required, to be submerged mounted at the inlet or outlet of the side channels, but at the same time to be possible to be raised easily for purposes of maintenance and cleaning, and, of course, economical aspects must be considered in the early phase of the machines selection.
Based on the above criteria, a simple non-regulated axial propeller was chosen to be designed for the case under consideration.
3.4 Detailed design of the turbine
3.4.1 Velocity triangles and design equations
A more comprehensive approach using the method of the velocity triangles and calculating the turbine hydraulic losses was applied [18, 20] and the associated system of equations was included in the dynamic model. The simplest approach to the analysis and design of a hydraulic turbine is to assume that the flow conditions at the mean radius represent the flow at all radii. This two-dimensional analysis can provide a reasonable approximation of the actual flow if the ratio of the blade height to mean radius is small. The below assumptions were made
- Water enters the turbine in the axial direction.
- The axial component of the flow velocity is constant.
- At design point, the flow velocity at the outlet is completely axial.
- Mean radius is constant, and the radius of the tip and hub was taken equal to 1 and 0.5 m, respectively.
- 16 guide vanes and 4 runner blades were considered
The rotational speed at the BEP can be either determined based on the Cordier curve or fixed on a certain value. The flow through a reaction axial machine should accelerate, but this was not the case if the speed of rotation was calculated based on the Cordier diagram. On the contrary, a rotational speed could be found above which the flow starts to accelerate, and this occurred above 25 rpm. Additionally, restrictions coming from the design of the electrical machine must be taken into consideration in the final selection.
3.4.2 Transient process modelling
The rotational speed, N in rpm or ω in rad/s, will be changed during the lock process, which will lead to a better performance of the machine due to the variation of the flow rate and hydraulic head. At that phase of the study, the transient speed of rotation is following the similarity law of (15). Therefore, the turbines will always operate at the BEP resulting in high and constant efficiency during the lock process.
 (15)
(15)
The detailed design of the turbines revealed a slight different filling time, compared with the results of the simple turbine model which gave a time equal to 480 s. The evolution of the flow and gross head together with the corresponding evolution of the potential power and the mechanical power is given in Fig. 6.

Evolution of
(a) The flow rate, Qi, and gross head, ΔH, and (b) The turbine power, P, with the detailed turbine model
The total energy produced is 18.51 MJ (or 47.38% of the potential energy). The amount calculated with the detailed model is less than the one predicted by the simple turbine model, because the losses in the machine are being considered, whereas in the simple model the efficiency was considered to be equal to 100%. The efficiency is being calculated by (16) and was found to be constant around 80%.
 (16)
(16)
3.4.3 Turbine characteristic curves
The characteristic curves (Fig. 7) of the hydraulic machine can be reproduced by performing simulations with constant flow rates, in the range of 1–15 m3/s, and linearly varying speed of rotation from 0 to 200 rpm. The rotational speed at the design point was always 50 rpm, and the hub and tip radius of 0.5 and 1 m, respectively. The best hydraulic efficiency of the turbine obtained in Fig. 7d is consistent with the values obtained in recent numerical simulations concerning very low head turbines and a little bit higher than the efficiency experimentally obtained in recent works [21-23].

Turbine characteristic curves for different flow rates
(a) Power output, (b) Turbine hydraulic head, (c) Torque, (d) Efficiency
At a constant flow rate, the hydraulic head, the torque and the power can be described as a function of the rotational speed
 (17)
(17)
 (18)
(18)
 (19)
(19)
where A, B and C are constants with the corresponding units. The constants depend on the flow rate, following perfectly a linear or power law. Therefore, the characteristic curves can be expressed as a function of the speed of rotation and the flow rate (Table 1). Dividing the mechanical and the hydraulic power, an equation for the efficiency can also be produced.
 (20)
(20)
From Fig. 7a, it is obvious that for every flow rate there is an optimum speed of rotation, Nopt, for which the turbine can produce the maximum power. This speed can be found by taking the maximum of the power output. The equation below can be used as a tool (Fig. 8) for tracking the maximum power for a specific flow rate and imposing the optimum rotational speed in the Simulink model (instead of the law of similarity).
 (21)
(21)

Maximum power tracking
Compared with the results for which the law of similarity for the imposed rotational speed was used, there are slight differences in the filling time and the amount of energy being recuperated. The total energy produced was 18.61 MJ (or 47.64% of the potential energy).
4 Electromechanical conversion
The electromechanical conversion should transform the hydraulic power extracted by the turbine first to electrical power through the mechanical coupling between these two components. Then, the generated electrical energy is either delivered to the grid or to a local utility. As introduced above, the turbine will be installed at the inlet or outlet of the side conduits in order to avoid any civil engineering modification and its rotation speed during the operation will not be constant. Therefore, whatever the chosen generator and the purpose of the conversion, static converters have to be used to generate a final voltage with constant amplitude and frequency. Thus, the architecture of the electromechanical conversion device is similar to those used in wind turbines or more specifically in tidal turbines at variable speed [24-27]. The main differences are relative to the generator to be used and to the most appropriate control for the application studied, due to the atypical character of flow of water as a function of time.
In the following sections, the overall scheme of the electromechanical conversion is first described. Then, the designed and sized electrical generator is introduced as well as the control principle adopted.
Finally, the models of the different mechanical and electrical parts are coupled and the whole system is simulated by applying the used control with the aim of extracting the maximum power using variable speed turbine-generator.
4.1 Electromechanical system
The whole electromechanical system is illustrated in Fig. 9. It constitutes of an electrical generator driven by the turbine and two static converters, i.e. a rectifier and an inverter for the converters 1 and 2, respectively.

Electrical system illustration
In this system, the generator can be either immersed integrated with the turbine or out of water with its shaft mechanically coupled to the turbine through different devices. In our case, the first solution is chosen for reasons of compactness and simplifications of mechanical parts. Besides, in order to be able to control the energy flows and the different electrical quantities, the two static converters must be controllable and therefore, conventional PWM-controlled converters are used. As introduced previously, the flow rate in the channel is initially controlled by adjusting the opening of the valve. The extracted power of the turbine varies with the flow rate and turbine rotational speed. The control of converter 1 (Fig. 9) leads then to controlling the torque created by the electrical machine and thus adjusting the turbine speed at the optimal operation points which depend on the turbine design parameters as explained in the last section. This process is therefore similar to maximum power point tracking (MPPT) in a wind turbine control [28].
The converter 2, placed between the DC bus and the electrical grid, leads to controlling the DC bus voltage at a constant value and the reactive power on the grid with sinusoidal current absorption. The control of the DC bus voltage leads to having the electrical grid power equal to the power generated by the electrical machine.
4.2 Permanent magnet Vernier generator
Following the design of the turbine, the chosen generator obviously has to fulfil some specifications and constraints. Indeed, its rated speed has to be low in order to avoid any mechanical gearbox and its volume must be small enough in order to be housed in the available interior volume of the turbine. These two constraints cannot be satisfied at the same time by a classical direct driven permanent magnet synchronous machine (PMSM) as it requires a large pole pair number to satisfy a rated low-speed operation at standard frequency leading to a large diameter. Therefore, to reach a high torque at low-speed operation while ensuring frequency of the electrical variables at standard value, a PM Vernier generator machine (PMVM) is designed, which has a simple structure compared with classical PMSM [29, 30]. The designed prototype is illustrated in Fig. 10. It is an inner stator outer rotor which provides the possibility to integrate the turbine blades into the latter.

Permanent magnet vernier machine
In PMVM, the electromagnetic energy conversion is based on the interaction of the armature magnetic field with one of the rotating magnets which is modulated by the air gap permeance due to the open stator slots. Thus, to reach a continuous energy conversion at a synchronous speed, a special relationship among the rotor PM pole pair number pr, the stator winding pole pair number, ps, and the stator slots number, Ns, should be satisfied to obtain constant torque with low ripples.
 (22)
(22)
Then, the synchronous speed, Ω, is linked to the stator frequency, ω, by Ω = ω/pr.
With the specifications of the studied application, an inner stator outer rotor prototype generator at 50 rpm and 36.6 Hz (pr = 44, ps = 4 and Ns = 48) has been analytically designed, optimised and verified by finite element analysis method [16].
5 System control and performance
To study the behaviour of the whole system, a simulation model of the electromechanical conversion system is built.
5.1 Permanent magnet Vernier generator model and control
From the global point of view, the operation of the PMVM is quite similar to the PMSM. Therefore, its three-phase lumped parameter model is identical to one of the synchronous machine and can be expressed in dq rotating reference frame as follows [31]
 (23)
(23)
where v and i represent the voltage and current, respectively, R is the winding resistance, ΨPM is the PM flux linkage, pr is the rotor pole pair number of the machine. ωe is the electrical rotational speed, ωm is the mechanical rotational speed, Tm is the load torque and Te is the generator torque. Finally, fv represents the viscous damping and J is the system total inertia of the rotating parts. Furthermore, as the magnets are rotor surface mounted, no air gap magnetic saliency, that can modulate the stator inductances, is present, i.e. they are constant with respects to the rotor position. Hence, the dq axis inductances are identical (Ld = Lq).
The values of the designed machine dq model parameters are identified from the numerical model of the optimised prototype and given in Table 2. This model is used to develop a control strategy based on classical vector current control (or field oriented control).
| dq-axes inductances, Ld = Lq | 4.2 mH |
| flux, ΨPM | 1.41 Wb |
| system total inertia, J | 1300 kg m2 |
| pole pair number, pr | 44 |
| generator stator resistance, R | 0.1 Ω |
Fig. 11 shows the control scheme for the generator-side converter. As in the case of conventional surface mounted PMSM, the d-axis current reference is set to zero to minimise the copper losses of the generator [32]. The q-axis current reference is calculated by the speed loop controller. The input of the latter, i.e. speed reference, is obtained from the MPPT algorithm based on the measured or estimated flow rate.

Generator-side converter control structure
5.2 Grid-side model and control
The grid-side model is like the generator one when RL filter model is chosen. The three-phase voltages and currents of the grid side can also be modelled in a dq reference frame as follows [33]
 (24)
(24)
where the subscripts g and i denote the grid and the inverter side, rf and lf are the grid-side resistance and inductance, their used values in simulations are 0.01 Ω and 1 mH, respectively. Udi and Uqi are the inverter side dq axis voltages, Udg and Uqg are the grid-side dq axis voltages, idg and iqg are the grid-side dq axis currents, ωg is the grid-side frequency which can be determined by Phase Lock Loop (PLL method) [34]. Like in the generator-side converter, the dq axis currents and voltages are decoupled. This characteristic provides an effective mean for the independent control of the active and reactive powers of the system. The grid-side active power, Pg, and reactive power, Qg, can be calculated by (25) [33]. Qg is controlled to zero to achieve unity power factor control.
 (25)
(25)
Fig. 12 shows the grid-side converter control structure. It contains two cascaded control loops. The inner loops control the grid currents or grid power and the outer loops control the DC-link voltage and the reactive power. In order to transfer the maximum available power to the grid from the DC bus, the voltage of the DC bus should be controlled at a constant reference value. In the inner current control loop, the dq-axes current references are calculated by (25). The outer loop gives out the active and reactive power references. The dq axis voltages are obtained from the transformation of the measured grid-side voltage.

Grid-side converter control structure
5.3 Simulation results
As already mentioned, the valves are controlled in four steps in a real typical lock and several scenarios are possible; either adding the turbine without changing the valve opening procedure, or letting the same procedure with different opening times or opening the valve in one step. The different processes of valve opening will be discussed in detail with respect to energy extracting.
The dynamic simulation equations described in the previous section are used to build an average model in Matlab/Simulink®. The grid-side energy is compared for different operation valve process.
Fig. 13 shows the simulation results of one turbine when the valves are opened in one step. From the flow rate variation curve, it is known that the water in lock can be filled or drained in ∼480 s. The measured rotational speed and the DC bus voltage follow their reference quite well. Grid-side unity power factor is achieved as the reactive power is kept at zero. It indicates that the control parameters are tuned very well.

Dynamic simulation results of one turbine for valve opened instantaneously
The cases when the valve is controlled to be opened in four steps with different opening times are also investigated. Fig. 14 shows the comparison of the flow rate for the different valve opening process. It can be seen that the peak flow rate becomes smaller when the valve is opened in four steps. The cycle time increases by about 50 s for opening steps equal to 60 and 120 s for a step of 120 s compared to the case where the valves were opened instantaneously. The peak flow rate in the channel decreases when the valves are opened in a longer time. As a reason for that, the draining or filling time increases. It reveals that the operation time for ship passing may increase one or two minutes once the turbine-generator system installed if the valve is opened in four steps. Furthermore, in terms of energy delivered to the grid, Fig. 15 illustrates the grid-side energy comparison for the three cases. As expected, it shows that opening the valves in one step is the best solution as it can deliver more power to the grid side.

Flow rate comparison for different valve opening process

Grid-side energy comparison for one operation (filling and draining water)
These results show that it is possible to convert the hydraulic energy of the canal lock filling or draining into electrical energy in an efficient way using an MPPT control. However, the energy delivered to the grid is intermittent and varies quickly. It is not suitable to inject the produced energy directly into the grid. Therefore, an energy storage system (ESS) is needed to smooth the power profile.
6 Energy storage system
The canal lock available energy is strongly intermittent and can lead, in case of a more powerful system, to a non-negligible perturbation at the grid connection. To reduce potential grid-side power oscillations, ESS is adopted to smooth the power fluctuation.
The system topology with ESS is shown in Fig. 16. The latter is constituted of both batteries and supercapacitors. Indeed, the battery has high energy density and low power density characteristics while supercapacitors have opposite characteristics. Therefore, they can compensate each other and can be of great interest in the case of the studied application as explained above. Flow battery type is adopted as it has flexible energy, high power density capability and long-service life cycle. Furthermore, its self-discharge effect is very small [35].

System illustrations with ESS
6.1 Supercapacitors and DC–DC converters modelling
The supercapacitor is modelled as RC circuit. When charging, the voltage at its terminals can be deduced through the following relation
 (26)
(26)
where isup is the supercapacitor current, and Rsup is the supercapacitor resistance.
While connected to the buck DC–DC converter, a second equation must be applied to calculate the dynamics of the current isup:
 (27)
(27)
L is the buffer inductor inductance and Dcyc is the applied time-dependent duty cycle for the converter.
The above two equations can be used to build a dynamic average model for the coupling DC–DC converter/supercapacitors.
6.2 Battery modelling
The vanadium redox flow battery (VRB) technology is chosen and its model presented in this paper is mainly based on the reference [35, 36].
Fig. 17 shows the flow battery equivalent circuit model where the stack current Istack and stack voltage Vstack represent the battery cell-stack internal current and electromotive force that permit to calculate the battery state of charge. The battery terminal voltage and current are expressed as Vbattery and Ibattery. The transient component associated with the electrode capacitance is modelled by Celetrode.

VRB equivalent circuit model [36]
The losses are taken into account by the internal resistances Rreaction and Rresistive while the parasitic resistance Rfixed allows modelling the stack bypass current. The power losses due to the circulation pump and the system controller are represented by the loss current Ipump. Finally, the switch on the parasitic branch is used to account for the battery standby mode. The parameter calculation process is detailed in [34].
6.3 ESS power flow control
In order to reduce the grid-side power oscillation, it is assumed to control the grid-side power as constant during the day. The ESS power (positive for the charge mode) is set to compensate for the difference between the available power supply at DC bus PG and grid power demand as follows
 (28)
(28)
To be able to achieve a good control strategy in which the battery is mitigated of stresses, the high-frequency part of the power should be sent to the supercapacitor and the low-frequency part to the batteries. Then, the power flow in the battery and the supercapacitor will be determined using a low pass filter control strategy as shown in Fig. 18.

ESS power flow control
Based on the power references, the reference currents of the battery and the supercapacitor can be calculated as the DC bus voltage is controllable. The two current references will be then controlled by their corresponding PI controller. The outputs of the latter are the corresponding converter voltages which will be used to calculate the modulation duty cycles of the converters.
6.4 Simulation results with ESS
The assumption that there is only one operation of filling and draining water per hour in the day is made and two operations are simulated. The power flow in the system is shown in Fig. 19. The blue line shows the energy produced by the generator. The grid-side power will be kept at the average level for one hour. At the beginning of each cycle, one part of the generator produced power will be transferred to the grid. Then, the rest power will be used to charge the battery and the supercapacitor. It can be seen that the supercapacitor charged faster than the battery. When the generator power is zero, the battery will be discharged to keep the grid-side power as smooth as possible.

Power flow in the system
7 Conclusion
This paper presents the whole system of canal lock energy exploration for a facility located in the north of France with an available hydraulic head of 3 m by installing submerged turbines on the channel's flow. Up to four turbines can be installed at each facility. All results presented above are for one turbine and during filling or draining the lock.
Hydraulic canal lock modelling and design of a non-regulated axial propeller turbine are detailed. For the electrical part, a permanent magnet Vernier (PMVM) is designed and optimised for this project. The variable generator rotational speed (0–50 rpm) is controlled depending on the estimated current flow (0–11 m3/s) to achieve maximum power tracking. The aim of grid-side control is to keep the DC bus voltage constant. Therefore, the active power produced by the generator can be totally transferred to the grid side. The reactive power is controlled as zero. In addition, ESS is applied to control the power flow inside the system. Hence, the power can be smoothed for the grid-side power integration.
The priority operation of canal lock facility is to facilitate the navigation of ships. Therefore, major civil engineer works, which will result in shutting down the facility, cannot be implemented to maximise the energy exploration. This limits the total harnessed energy. The hydraulic system can achieve efficiency by about 47%. In the electrical part simulation, the generator core losses, generator mechanical losses and converter losses are not introduced in the model for simplicity in a classical way. The electrical part efficiency is estimated at about 90%. Therefore, the total energy per turbine transferred to the grid is ∼40% of the available theoretical energy. The total recovered energy depends on the total number of turbines to be installed, and since only the cases of installing two or four machines is being considered (because it is important always to retain the symmetry of the canal lock and not to disturb the stability of the ships during filling/draining the lock), the total energy produced is around 62.5 MJ per operation (fill or drain) or 125 MJ in a full-operation cycle. As this sum of energy is the additional benefit of ship passing, canal lock energy extracting should not be underestimated.
The present study was conducted to show the technical feasibility of converting available hydropower to electrical energy on canal locks during raising and lowering ships. It was carried out on a given lock, with a limited number of ships passing the lock per day, whose information is available. Moreover, it was conducted in a way that does not change the current operation of the lock. Therefore, a serious analysis of economic ‘profitability’ cannot be conducted only on the basis of the results presented. Apart from a pure sustainable development aspect, the economic study must consider the number of daily operations of the lock, its day-to-day working scale, the development of a forecasting strategy to optimise the energy recovered by operation etc. These points could be the subject of an extensive complementary work.
The next step of the research project is to focus on a more detailed study of the channel power losses using numerical modelling method. Additionally, a scaled 1 kW turbine-generator system is under developing for validating the developed dynamic model.
8 Acknowledgments
The project carried out in close collaboration by two research laboratories of Ecole Nationale Supérieure d'Arts et Métiers (ENSAM) and University of Lille, one specialised in turbomachinery (LMFL) and one in electromagnetic systems (L2EP), with the support of Electricité de France (EDF), the French electric utility company, and Voies Navigables de France (VNF), the French navigation authority responsible for the management of the majority of France's inland waterways network and the associated facilities. The work financially supported by the Region Hauts de France, EDF and VNF.
9 References
How the Water Locks of Panama Canal Work?
One of the major artificial waterways in the world, Panama Canal connects the Atlantic Ocean and the Pacific Ocean, cutting across the Isthmus of Panama- a narrow strip that separates the Caribbean Sea from the Pacific Ocean.
Completed construction in August 1914, the 77 km-long Panama Canal helps ships sailing between the east and west coasts of the US to shorten their journey by 15,000 km. Similarly, the canal saves up to 3,700 km for vessels transiting between Europe and East Asia.
Currently, the Panama Canal plays a significant role in the US economy since it handles a substantial share of US shipping. In the fiscal year 2017, the canal witnessed the passage of a total of 13,548 vessels, carrying 403.8 million Panama Canal tons of cargo.
Do you know about these interesting facts about the Panama Canal?
Geographically, the oceans that Panama Canal connects with are not at the same level; the Pacific Ocean lies a little higher than the Atlantic Ocean.
This difference in the sea level requires ships to get up over the terrain of Panama- up to 26 meters above sea level- in order to reach the other end of the canal.
With the help of Lock Gates, the vessels entering the canal are lifted to a higher level and later dropped down to the sea level at the other end of the canal.
The Panama Water Lock System is considered to be one of the greatest engineering services undertaken at that time, purporting to the needs of the ships to save transit time.

Design of the Panama Canal Locks
The Panama Water Lock System consists of a total of three sets of locks-12 locks- to help vessels transit between the Atlantic and the Pacific Oceans via artificial lakes and channels.
Before the canal expansion, which was completed in 2016, the canal had two lines with two sets of the lock at both ends of the canal.
The expansion of the canal resulted in a third lane and a third set of locks that allow the entry of larger vessels.
The locks, located on the Atlantic and the Pacific sides, lift and lower the vessels to/ from the Panama Canal that is situated 26 metres from sea level.
On the Pacific side, the lock system features the two-chambered Miraflores Locks and the one-chambered Pedro Miguel Locks, while the three-chambered Gatun Locks sit on the Atlantic Side of the Panama Canal.
Since these three sets of locks are paired, two parallel flights of locks are located at each of the three lock sites, allowing the simultaneous movement of vessels in opposite directions.
However, in practice, only six massive pairs of locks are used by ships for transit now, and the ships move in one direction at a time due to safety constraints to cross the Culebra Cut.
It also means that the ships currently use both lanes of the lock only to move in one direction at a time.
The original locks of the Panama Canal are 33.53 meters (110 feet) wide, while each lock features a length of 320 meters (1,050 feet). The walls of each lock have a thickness ranges from 15 meters (at the base) to 3 meters (at the top).
The dimensions of the lock decide the size of a ship, which is also known as Panamax- that can pass through the canal. The third set of locks opened after the expansion project allows bigger vessels to cross the canal.
The new Panamax metrics, with the new locks, allows the ships with an overall length of 366 meters, a beam of 49 meters and a draft of 15.2 meters. The total lift, the capacity to raise or lower a vessel, of the locks are; Gatun locks-85 feet, Pedro Miguel locks-54 feet and Miraflores- between 64.5 feet and 43 feet due to the extreme tides.
The gates of the Panama Canal locks separate the champers, and are strong enough to hold thousands of litres of water. The water locks are filled or emptied in less than 10 minutes and each pair of lock gates takes two minutes to open.
The size of the Panama lock gates ranges from 14.33 to 24.99 meters and measures 2.13 meters in thickness. Each gate features two leaves that measure 19.81 meters in width and these leaves are close to a “V” shape with the point upstream, allowing the gates to handle the force of the water.
The gates are only opened when the water level is equal on both sides. A fender chain, weighing around 30,000 pounds, at the end of each lock prevents ships from ramming the gates before they open.
In order to let the vessels pass the lock, each chamber needs to be filled with 26,700,000 US gallons of water. The locks are operated using the gravity flow of water from lakes such as Gatún, Alajuela, and Miraflores.
The lock system includes 18 feet wide water culverts attached to it, performing the duty of carrying water from these lakes to the chambers to raise the vessels and from chambers to the next lock or the sea to lower the vessels.
Operated electrically, the entire process of the lock system is controlled from a control room located on the centre wall of the upper flight of locks.
The control rooms guide the vessels through the lock chambers using electric towing locomotives. Ships are pulled with the help of these machines, called “mules”, using a cable through the locks.
On average, ships require six of such mules, three on each side, when using the locks to enter or exit the canal.
Operation of the Panama Canal Locks
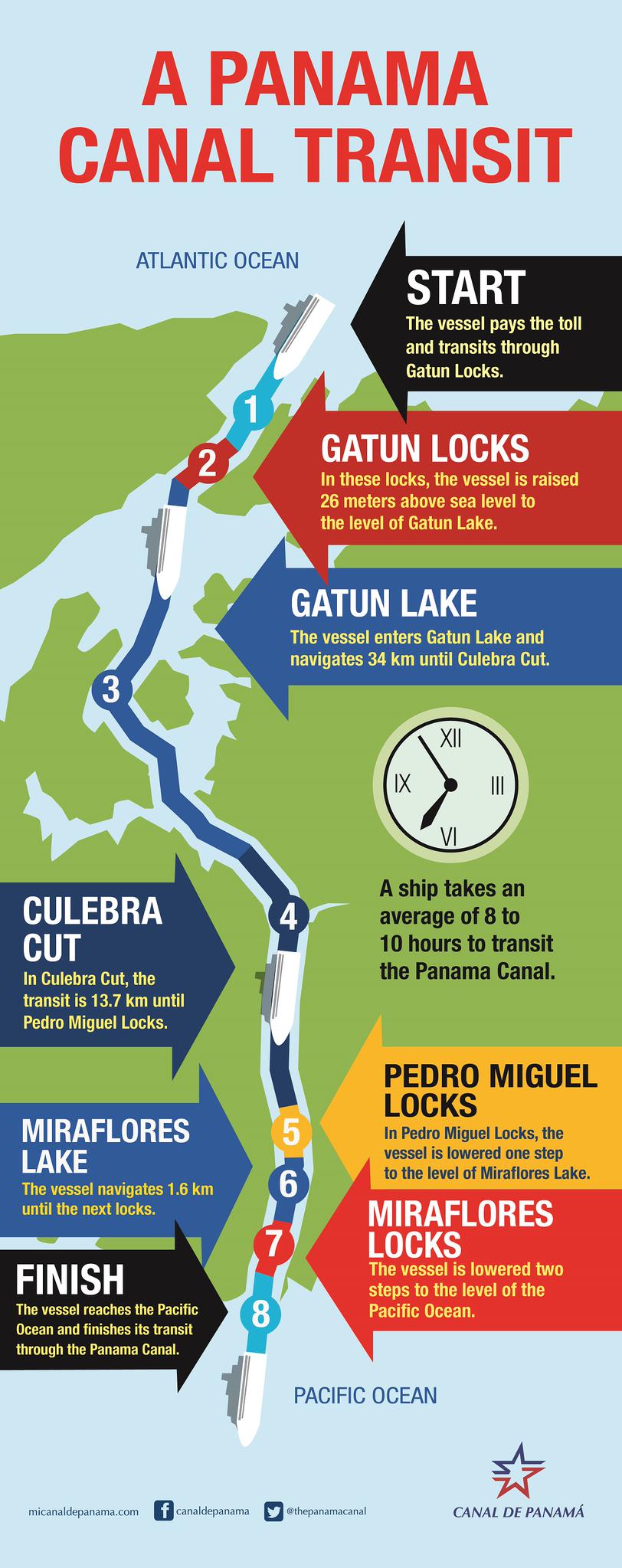
The whole operation of the Panama Water Lock System works can be described in a few steps:
1. The vessel approaches towards the lower chamber of the canal locks;
2. the valve of the first chamber opens and water flows by force of gravity from the higher chamber to the lowest one, bringing the water level to the sea level;
3. the locked gate opens to allow the ship into the chamber, and the gate closes behind it;
4. the valve of the next chamber is opened to increase the water level to that of the first chamber;
5. the gate of the lock is opened and the ship enters the next chamber;
6. The water level is equalized again and the ship finally exits the lock and enters the 77 km long canal.
At the other end of the canal, a similar process will be performed in order to lower the vessel to sea level.
In detail:
For a ship entering the canal from the Atlantic end, travelling in a southeast direction, the first entry will be into the first (sea level) lock chamber located at the Gatun Locks.
After the vessels entered the chamber, the watertight lock doors are closed by the lock-master and the valve is opened to allow the flow of water from the adjacent second lock chamber, 28 feet above sea level.
Water flows through underground pipes into the first chamber until the water levels are equal.
However, no pumps are used here; the entire operation of equalizing the water levels between the locking chambers on the Panama Canal depends on the principles of gravity to move the water and on the fact that water seeks its own level.
When the water levels of two adjacent chambers are equal, the water stops flowing from the water culverts.
Once the water levels between the first and second chamber are the same, the valve gets closed by the lock-master and the watertight lock doors between the first lock chamber and the second lock chamber are opened subsequently.
This process allows the ship to proceed to the second lock chamber. The first operation is repeated then between the second lock chamber and the third lock chamber, which raises the ship to the level of Gatun Lake.
After the closure of the final valve and opening of the watertight lock door, the ship is raised 85 feet above sea level and is able to continue its journey to the Pacific.
The same process inversely is followed in order to send the ship back to sea level. At the Pedro Miguel Locks on the Pacific end of the canal, when the ship enters the first chamber, the watertight doors are closed and the valve gets opened on that lock chamber, allowing water to drain from the first lock chamber into the relatively lower second lock chamber.
After the water level between the two chambers is at the same level, the watertight doors are opened allowing the ship to continue to transmit down the Gaillard Cut to the Miraflores Locks, where the operation of lowering the ship to sea level is completed.
You may also like to read – 4th Engineer’s First Journey Through The Panama Canal
The Panama Canal is the shortcut between the Atlantic and the Pacific oceans. As the Earth's climate changes, the canal will face changes, too. It depends on rain, not seawater, to fill its locks, and changes in rainfall might mean the canal could run out of water.
STEVE INSKEEP, host:
A canal that changed the world is now having to change itself. The Panama Canal revolutionized shipping between the Atlantic and Pacific Oceans. This morning it's the focus of Climate Connections, our year-long series with National Geographic, because it could be affected by global warming. We have more, this morning, from NPR's Jon Hamilton.
JON HAMILTON: If you've ever bought shoes at Wal-Mart or bananas at Costco, there's a good chance they came through the Panama Canal on a cargo ship like the Maersk Dartford.
Mr. JORGE DE LA GUARDIA (Panama Canal Authority): We're looking at a Panama ship. It's going south.
HAMILTON: Jorge de la Guardia works for the Panama Canal authority. We're watching the Dartford squeeze through the Miraflores locks on her way from the Atlantic Ocean to the Pacific. Like thousands of ships around the world, the Dartford was built to what's become known as the Panamax standard, that's the maximum size that can still navigate the Panama Canal.
Mr. DE LA GUARDIA: Panama ship is defined as a ship of over 100 feet in the beam and they usually are from about 850 to 965 feet in length.
HAMILTON: The gap between the Dartford's steel hull and the lock's concrete wall is two feet. It's such a tight fit that pilots often use full power to force a ship into the lock like a cork into a wine bottle.
HAMILTON: Right now about four percent of all world trade passes through the Panama Canal. It's the short cut between the Atlantic and the Pacific. De la Guardia says Panamax ships like the Dartford pay about $250,000 for each crossing.
Mr. DE LA GUARDIA: Well, you know, the canal is the most important industry that Panama has. Because of the canal we have ports. The port activity is increasing tremendously.
HAMILTON: Ships pay to use the canal because the alternative is a 9000 mile detour around Cape Horn on the southern tip of South America. The only other route is way north through the Arctic, and so far ice has made that a risky option. The need for a global shortcut was why a French company started building the Panama Canal at the end of the 19th century. The U.S. finished it in 1914. The canal is critical to international trade, especially between the U.S. and China.
But there's a problem. International shipping companies are starting to use bigger ships because they're more efficient, and these new vessels are too big for the canal. So Panama is spending more than $5 billion on an expansion project. It includes a new set of locks that are much wider and deeper than the existing two sets. The project got underway officially last year.
(Soundbite of crowd cheering and fireworks)
HAMILTON: The expansion should be done by the canal's 100th birthday in 2014. That will solve the problem of accommodating bigger ships, but it's also creating a new problem: the canal depends on rain and that's where climate change comes in. The Panama Canal isn't just a channel between two oceans. In fact, it doesn't use ocean water. It runs on fresh water pouring in from 17 artificial interconnected lakes.
Mr. DE LA GUARDIA: Everything works by gravity.
HAMILTON: Jorge de la Guardia says the water flows down into a series of locks, or lanes, as they're sometimes called here. These locks gradually raise each ship 85 feet above sea level. De la Guardia says that takes a lot of water.
Mr. DE LA GUARDIA: Yeah, a transiter, a full transiter going from the Pacific or the Atlantic Oceans, from ocean to ocean will take about 55 million gallons of fresh water.
HAMILTON: And it's your job to make sure there's enough water to keep the ships moving?
Mr. DE LA GUARDIA: Yes, yes.
HAMILTON: The Panama Canal already consumes three times as much water in a day as the city of Los Angeles. When the new lane for big ships is built, the canal will need even more. The question is, will there be enough? Stanley Heckadon-Moreno works at the Smithsonian Tropical Research Institute in Panama City. He says the lakes that feed the canal are vulnerable to the climate fluctuation known as el Nino.
Mr. STANLEY HECKADON-MORENO (Smithsonian Tropical Research Institute): What if the theory of global warming were to increase the number of el Nino events which will bring greater and more devastating droughts to the isthmus and water will become definitely scarcer for the canal.
HAMILTON: El Ninos in 1997 and 1998 left the canal so short of water that ships had to unload part of their cargo to keep from running aground. It was the worst drought in the canals history and it disrupted shipping around the world. No one really knows whether climate change is going to make el Ninos more frequent, but Heckadon sees some ominous trends.
Mr. HECKADON-MORENO: Inside the canal watershed, inside the valley of the Chagres river, there has been an affect on that micro watershed, and there has been a decrease in rainfall.
HAMILTON: So far, that's probably got more to do with the huge number of trees cut down than with climate change. But the result is the same, and officials are worried. Carlos Vargas from the Canal Authority says the expansion plan allows for some climate variability.
Mr. CARLOS VARGAS (Panama Canal Authority, Manager, Meteorological and Hydrographic Branch): It is very important because we all know that the canal depends on water. If it doesn't rain we don't have enough water for the operation of the canal, so we have to take it very seriously.
HAMILTON: The plan calls for storing more water in lakes, and perhaps using less water to generate electric power. And the most important hedge against a water shortage is the new locks themselves. The ones in the lane for big ships will use a design that recycles 60 percent of the water.
(Soundbite of canal)
HAMILTON: Even so, Jorge de la Guardia from the Canal Authority says that if el Nino years come more frequently, the canal could still be in trouble. Solutions, like creating new lakes would cost a lot and destroy even more of the dwindling rain forest. But de la Guardia says Panamanians will probably do whatever it takes to keep water flowing to the canal.
Mr. DE LA GUARDIA: What I would love to see is that we make such good business with a third lane, that we make a fourth lane and then we'll need water, right away.
HAMILTON: Drought is just one way that climate change looms over the future of the Panama Canal. Rising seas could flood ports along the shipping routes that go through the canal. Extreme weather is another threat. When Hurricane Katrina delayed ships on the Mississippi River, they missed their slots to go through the canal. It created a huge traffic jam. And then there's that melting ice in the Arctic. It could make the Northern Passage a viable option for shipping. If the world gets warm enough, goods headed for the U.S. may skip Panama all together.
Jon Hamilton, NPR News.
(Soundbite of music)
INSKEEP: You can hear more stories in this series at npr.org/climateconnections, which is where you can also see videos of climate science in action. That's from public television's Wild Chronicles.
Copyright © 2008 NPR. All rights reserved. Visit our website terms of use and permissions pages at www.npr.org for further information.
NPR transcripts are created on a rush deadline by an NPR contractor. This text may not be in its final form and may be updated or revised in the future. Accuracy and availability may vary. The authoritative record of NPR’s programming is the audio record.
Canal Lock How To: An Essential Guide for Understanding How Locks Work - Narrowboat Nomad
Canal locks are an essential part of any canal system, allowing boats to navigate through changes in water level. A canal lock diagram can help people understand how these locks work and how they are constructed.
The basic design of a lock involves a chamber with gates at either end. When a boat enters the chamber, the gates are closed behind it, and water is either added or removed to raise or lower the boat to the level of the next stretch of canal. Canal lock diagrams often show the various components of the lock, including the gates, paddles, and winding gear used to operate them.
Understanding the mechanics of a canal lock can be useful for anyone interested in boating or canal travel. Canal lock diagrams can also be helpful for engineers and designers who are involved in the construction or maintenance of canal systems. By providing a clear visual representation of the lock’s components and operation, these diagrams can help ensure that locks are built and maintained correctly, and that boats can safely navigate through them.

Canal locks are an essential component of canal systems, allowing boats to travel up and down waterways with varying water levels. A lock is a watertight chamber that can be filled or emptied to raise or lower boats to the level of the water on the other side of a dam or other barrier.
Construction
Canal locks are typically constructed with stone or concrete walls and gates that can be opened and closed to control the flow of water. The gates are operated by a windlass or engine that raises and lowers them. The lock chamber is a watertight chamber that can be filled or emptied by opening and closing valves.
Operation
To operate a canal lock, a boat enters the chamber and the gates are closed behind it. Water is then either let in or drained out of the chamber until the water level inside the chamber is equal to the water level on the other side of the lock. The gates on the other side of the lock are then opened, allowing the boat to pass through.
Types of Canal Locks
There are several types of canal locks, including pound locks, flash locks, and staircase locks. Pound locks are the most common type and consist of a single chamber that can be filled or emptied to raise or lower boats. Flash locks are used on rivers and consist of a gate that can be opened to allow boats to pass through quickly. Staircase locks consist of a series of chambers that step up or down to accommodate changes in water levels.
Canal locks have been used for centuries and are still in use today. They have many advantages, including the ability to transport boats up and down rivers and canals, and the ability to control water levels in rivers and canals. Examples of famous canal locks include those on the Panama Canal and the Grand Canal in China.
Overall, canal locks are an important part of canal and river systems, using science and technology to allow boats to travel up and down waterways with varying water levels.
Lock Gates
Lock gates are an essential component of a canal lock that allows boats to move between different water levels. They are designed to control the water flow and maintain the water levels in the lock chamber. This section will discuss the types of lock gates and their construction.
Types of Lock Gates
There are two main types of lock gates: mitre gates and guillotine gates.
Mitre Gates
Mitre gates are the most common type of lock gate. They are hinged at the lock wall and open and close like a pair of doors. Mitre gates are made up of two leaves that meet at a 45-degree angle when closed. They are designed to withstand the water pressure and provide a watertight seal when closed.
Guillotine Gates
Guillotine gates are less common than mitre gates. They slide vertically in a groove and are raised and lowered by a windlass. Guillotine gates are used in narrow locks and are ideal for small boats.
Construction
Lock gates are made of wood, steel, or concrete. Wooden gates are the most common type of lock gate and are made of oak or teak. Steel gates are used in larger locks and are more durable than wooden gates. Concrete gates are used in modern locks and are more resistant to water pressure.
Lock gates consist of a top gate and a bottom gate. The top gate is usually larger than the bottom gate to accommodate the water pressure. The gates are operated by lock gear, which is a system of levers, chains, and pulleys. The gates are opened and closed by boaters using a windlass.
In conclusion, lock gates are an essential component of canal locks, allowing boats to move between different water levels. Mitre gates and guillotine gates are the two main types of lock gates, and they can be made of wood, steel, or concrete. The construction of lock gates is designed to withstand the water pressure and provide a watertight seal.
Lock Chambers
Lock chambers are an essential component of canal locks. They are the watertight chambers that allow boats to move between different water levels in a canal lock. Lock chambers are usually constructed from concrete or masonry, and they are designed to be strong enough to withstand the water pressure that is created when the lock is filled or emptied.
Rise and Fall of Water Levels
The rise and fall of water levels is the primary function of a lock chamber. When a boat enters the lock chamber, the gates are closed behind it, and the chamber is filled with water from the higher level. The water level in the chamber is then adjusted to match the level of the water on the other side of the lock gate. Once the water levels are equal, the gates on the other side of the chamber can be opened, and the boat can continue on its journey.
Emptying and Filling a Lock Chamber
Emptying and filling a lock chamber is a complex process that requires careful management of water levels and pressure. To empty a lock chamber, the paddles at the bottom of the chamber are opened, and the water is allowed to flow out. To fill the chamber, the paddles are closed, and the valves at the top of the chamber are opened to allow water to flow in.
The operation of a lock chamber requires a good understanding of water pressure and the principles of science and technology. Boaters must follow strict procedures when entering and leaving a lock chamber to ensure their safety and the safety of other watercraft.
Lock chambers are used in canal locks all over the world, from the Panama Canal to the Grand Canal in China. They are an essential part of the canal system, enabling boats to travel up and down hills and through areas of varying water levels.
In conclusion, lock chambers are an essential component of canal locks, enabling boats to move between different water levels. Their construction and operation require a good understanding of water pressure and the principles of science and technology. Boaters must follow strict procedures when entering and leaving a lock chamber to ensure their safety and the safety of other watercraft.
Lock Equipment
Lock equipment is an essential part of canal lock construction and operation. It includes various components such as lock gear, paddles, and valves. These components are crucial for the smooth operation of canal locks and allow boats to pass through the lock system without any damage or delay.
Lock Gear
Lock gear consists of all the mechanical components that are used to operate the lock gates. The lock gates are massive doors that are used to control the water level in the lock chamber, allowing boats to enter and exit the lock. The lock gear includes various components such as windlasses, capstans, and chains that are used to open and close the lock gates.
Paddles
Paddles are another critical component of lock equipment. They are used to control the flow of water into and out of the lock chamber. The paddles are located on the lock gates and are operated manually or electrically. When the paddles are opened, water flows into or out of the lock chamber, raising or lowering the water level to match the water level on the other side of the lock.
Valves
Valves are used to control the water flow in the lock chamber. They are located at the bottom of the lock chamber and are used to fill or empty the lock chamber with water. The valves are operated manually or electrically and are designed to be watertight to prevent water leaks.
Overall, lock equipment is an essential part of the canal lock system. It allows boats to pass through the lock system safely and efficiently, and it is crucial for the construction and operation of canal locks worldwide. Whether you are a boater or a lock operator, understanding the lock equipment is essential to ensure a smooth and safe passage through the canal lock system.
Lock Operation
Canal locks are an essential component of canal systems, allowing boats to navigate through changes in water levels. Lock operation involves the use of gates, valves, and other mechanisms to control water flow and boat movement.
Entering a Lock
When a boat approaches a lock, it must first wait for any boats currently in the lock to exit. Once the lock is clear, the boat can enter. The boat must then manoeuvre into the lock chamber and moor up using the balance beams and bollards provided.
The upstream gate is then closed, and the lock is filled with water using the ground paddles. The throttle is used to control the flow of water, and the boat rises to the level of the upstream canal. Once the water level has equalized, the upstream gate can be opened.
Exiting a Lock
When a boat is ready to exit a lock, it must first wait for any boats approaching from the upstream canal. Once the lock is clear, the downstream gate is opened, and the boat can exit. The boat must then manoeuvre out of the lock chamber and continue downstream.
The downstream gate is then closed, and the lock is emptied of water using the ground paddles. The throttle is used to control the flow of water, and the boat descends to the level of the downstream canal. Once the water level has equalized, the downstream gate can be opened.
Lock operation is a critical aspect of canal navigation, and it requires careful attention to detail to ensure that boats can move safely and efficiently through the canal system. Construction and maintenance of locks are also essential to ensure that they remain in good working order, with features such as spillways and fish ladders helping to maintain the natural ecosystem of the river.
Pumped Storage Hydropower
Learn More
What is Pumped Storage Hydropower?
Pumped storage hydropower (PSH) is a type of hydroelectric energy storage. It is a configuration of two water reservoirs at different elevations that can generate power as water moves down from one to the other (discharge), passing through a turbine. The system also requires power as it pumps water back into the upper reservoir (recharge). PSH acts similarly to a giant battery, because it can store power and then release it when needed. The Department of Energy's "Pumped Storage Hydropower" video explains how pumped storage works.
The first known use cases of PSH were found in Italy and Switzerland in the 1890s, and PSH was first used in the United States in 1930. Now, PSH facilities can be found all around the world! According to the 2023 edition of the Hydropower Market Report, PSH currently accounts for 96% of all utility-scale energy storage in the United States. America currently has 43 PSH plants and has the potential to add enough new PSH plants to more than double its current PSH capacity.
Video Url
Pumped storage hydropower is the most dominant form of energy storage on the electric grid today. It also plays an important role in bringing more renewable resources onto the grid.
U.S. Department of Energy
Open-Loop Versus Closed-Loop Pumped Storage Hydropower
PSH can be characterized as open-loop or closed-loop. Open-loop PSH has an ongoing hydrologic connection to a natural body of water. With closed-loop PSH, reservoirs are not connected to an outside body of water.
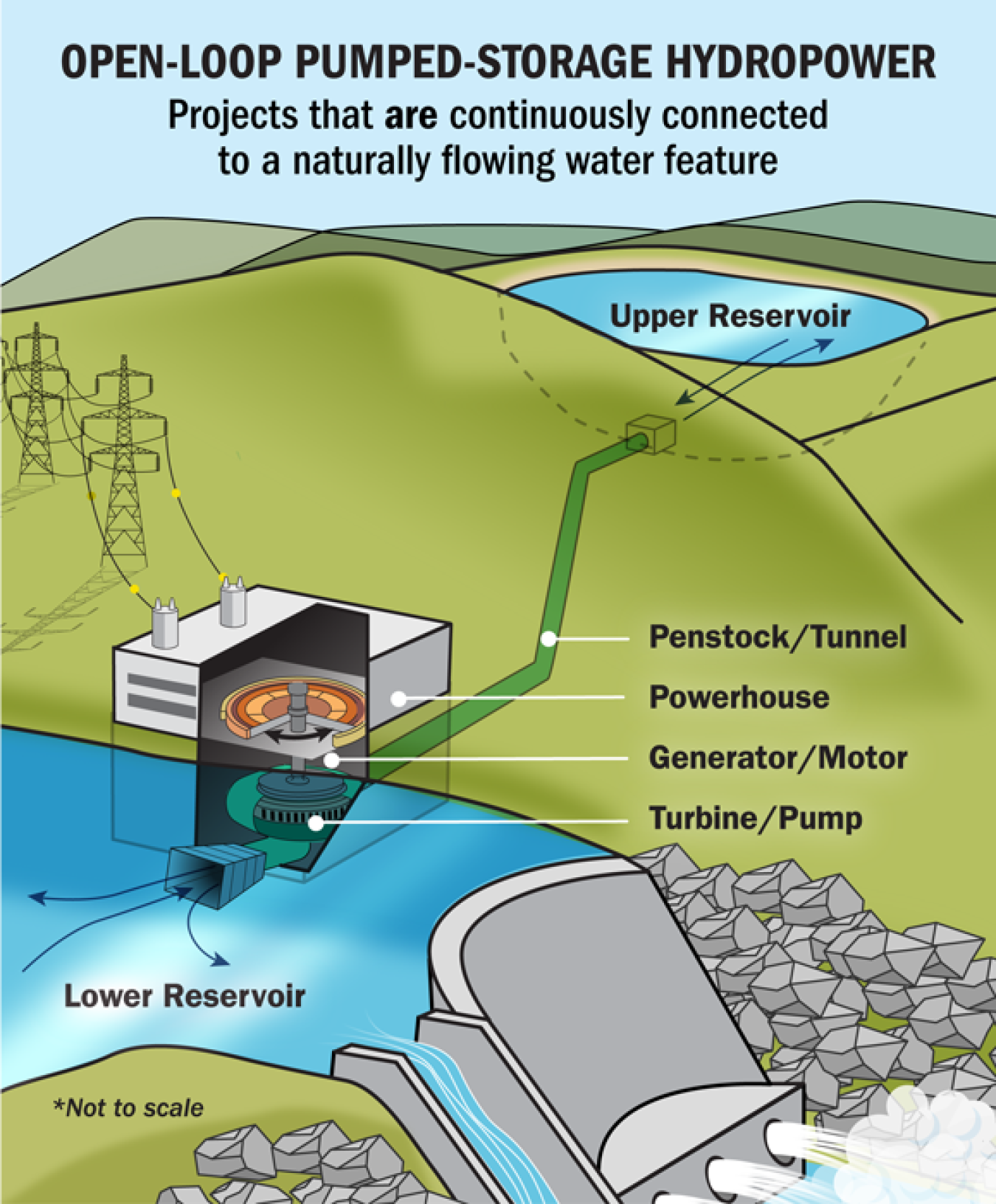
Open-loop pumped storage hydropower systems connect a reservoir to a naturally flowing water feature via a tunnel, using a turbine/pump and generator/motor to move water and create electricity.
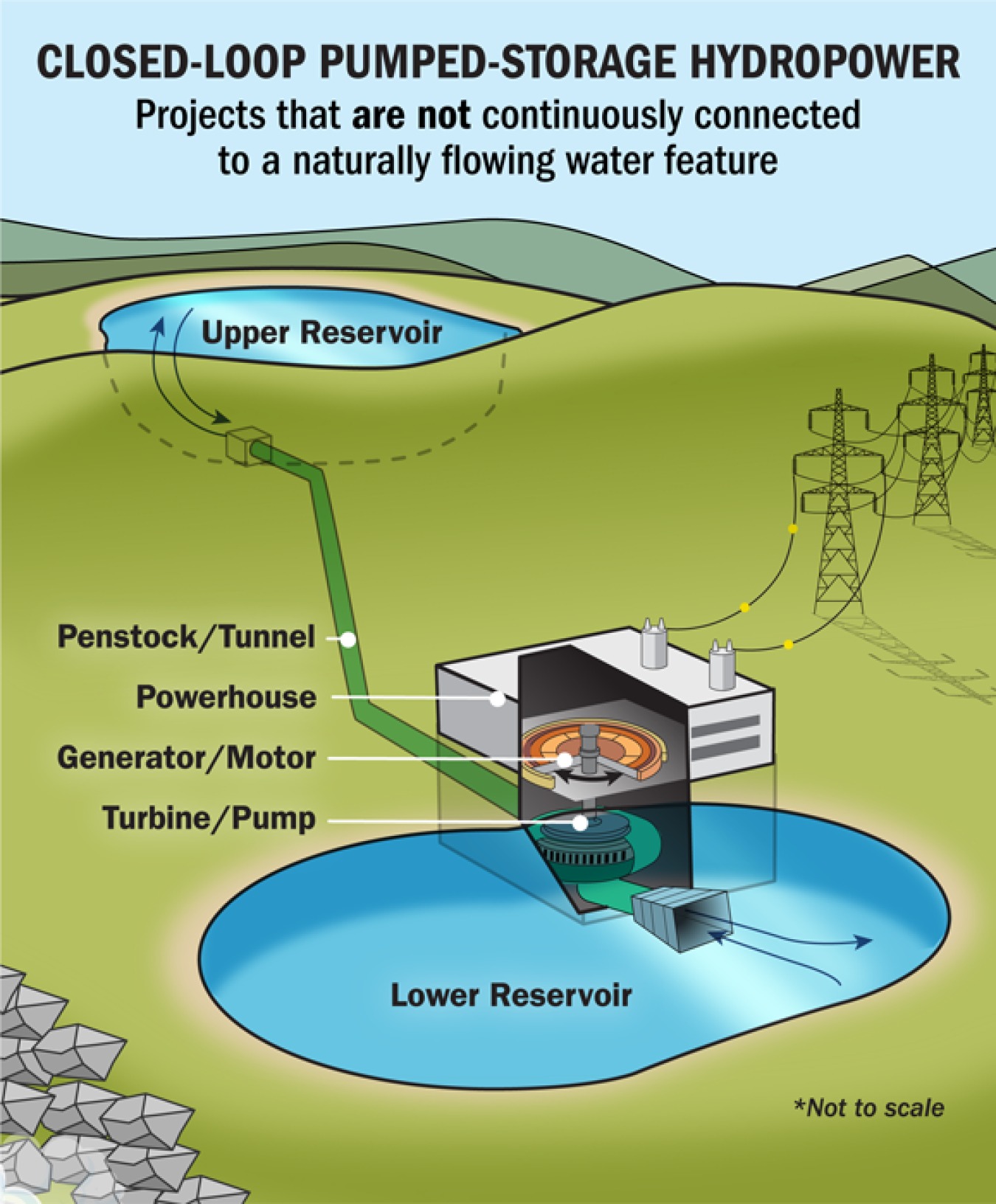
Closed-loop pumped storage hydropower systems connect two reservoirs without flowing water features via a tunnel, using a turbine/pump and generator/motor to move water and create electricity.
The Water Power Technologies Office (WPTO) invests in innovative PSH technologies and research to understand and determine the value of the potential benefits of existing and prospective advanced PSH facilities. Through the HydroWIRES Initiative, WPTO is currently working on projects designed to evaluate and expand hydropower and PSH’s contribution to grid resilience and reliability.
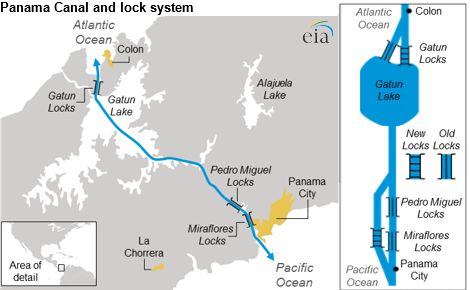
 Click to enlarge
Click to enlarge

No comments:
Post a Comment