UAV Shape Adaptive Dynamics Development and Control Design Surfs Powerlines

 

PowerLine Unmanned Surfer (PLUS): Shape Adaptive Dynamics Development and Control Design

Electrical Engineering and Systems Science > Systems and Control

[Submitted on 9 May 2024]

Ujjval Patel, Francis Phillips, Todd Henry, Imraan Faruque

This paper introduces the powerline unmanned surfer (PLUS) concept to extend the limited endurance of fixed wing unmanned aerial vehicles (UAVs) via in-flight energy harvesting from overhead electrical distribution power lines, and develops the flight dynamics and control framework to support centimeter-scale longitudinal powerline frequency tracking.

The dynamics framework models the UAV's shape adaptive structure, aerodynamic forces, and control inputs, and applies the coupled flight mechanics framework to low clearance tracking of powerline contours. This study develops a "trajectory to shape-adaptive UAV" controller design approach for longitudinal powerline tracking through local spatial frequency matching. The frequency-matching approach dynamically regulates the aircraft modes' frequency to the powerline catenary spatial frequency using a generalized parameter linearization approach.

Performance is assessed on an example UAV implementing camber and thickness morphing by quantifying clearance distance from neighborhood to high voltage powerline environments and across span and chord combinations. This approach achieves alternating periods of low-clearance tracking and antiphase oscillation, with 34% of the powerline having tracking error less than 1m. Airfoil thickness increase has a stronger effect over Phugoid mode wavelength than thickness decrease. Wingspan, chord, and powerline parameter sensitivities are quantified, providing a foundation for near-field long-distance powerline tracking and energy harvesting.

Comments:	11 pages, 19 figures
Subjects:	Systems and Control (eess.SY)
Cite as:	arXiv:2405.06006 [eess.SY]
	(or arXiv:2405.06006v1 [eess.SY] for this version)
	https://doi.org/10.48550/arXiv.2405.06006

Submission history

From: Ujjval Patel [view email]
[v1] Thu, 9 May 2024 17:58:05 UTC (9,015 KB)

 Summary

The paper presents a novel concept called the Powerline Unmanned Surfer (PLUS) that aims to extend the endurance of fixed-wing unmanned aerial vehicles (UAVs) by enabling in-flight energy harvesting from overhead electrical power lines. The main challenges addressed in this study are the development of a flight dynamics and control framework to support precise longitudinal powerline frequency tracking.

Key points:

1. The dynamics framework models the UAV's shape-adaptive structure, aerodynamic forces, and control inputs for low-clearance tracking of powerline contours.
2. A "trajectory to shape-adaptive UAV" controller design approach is developed for longitudinal powerline tracking through local spatial frequency matching. This approach dynamically regulates the aircraft modes' frequency to match the powerline catenary spatial frequency.
3. Performance is assessed on an example UAV implementing camber and thickness morphing by quantifying clearance distance across different powerline environments and aircraft parameters.
4. The approach achieves alternating periods of low-clearance tracking and antiphase oscillation, with 34% of the powerline having a tracking error less than 1m.
5. Airfoil thickness increase has a stronger effect on the Phugoid mode wavelength than thickness decrease. Wingspan, chord, and powerline parameter sensitivities are quantified.

The study provides a foundation for near-field, long-distance powerline tracking and energy harvesting using shape-adaptive UAVs. The dynamics-integrated UAV design approach, focusing on mission-specific trajectory requirements, offers a new perspective on designing UAVs for challenging missions such as powerline tracking.

Artifacts, Real Time Implementation

The paper does not mention any specific artifacts for concept verification or real-time implementation. However, there are a few aspects of the study that suggest the potential for experimental validation and real-time implementation:

1. Experimental identification of the structural actuation system:
   - The study includes an experiment where a representative servo actuation system for thickness morphing is manufactured and tested.
   - The servo's response to a multi-step input command is recorded, and the input/output signals are used to identify the system's transfer function.
   - This experimental work indicates that the authors have developed physical prototypes of the shape-adaptive actuation system, which could be used for further concept verification.

2. High-fidelity simulations:
   - The simulations are performed using a high-fidelity nonlinear shape-adaptive aircraft model in MATLAB.
   - The use of high-fidelity models suggests that the simulation framework could be adapted for real-time implementation, possibly using hardware-in-the-loop (HIL) testing or rapid prototyping systems.

3. Parameter space exploration:
   - The extensive parameter space exploration conducted in the study provides valuable insights into the relationships between aircraft parameters, powerline geometries, and shape adaptation requirements.
   - These insights could guide the design and development of physical prototypes for concept verification and real-time testing.

Although the paper does not explicitly mention real-time implementation or flight tests, the experimental work on the structural actuation system and the high-fidelity simulations suggest that the authors have laid the groundwork for potential concept verification and real-time implementation in the future. However, further research and development would be necessary to bridge the gap between the simulation results and a fully functional, real-time implementation of the PLUS system.

To move towards concept verification and real-time implementation, the following steps could be considered:

1. Development of a complete physical prototype of the shape-adaptive UAV.
2. Integration of the control algorithms with the UAV's onboard systems.
3. Validation of the control algorithms and shape adaptation mechanisms through HIL testing and real-time simulations.
4. Conducting flight tests in a controlled environment to assess the system's performance and robustness.
5. Refinement of the control algorithms and hardware based on the flight test results.

While the paper does not provide direct evidence of artifacts for concept verification or real-time implementation, the research presented in the study forms a solid foundation for future work in these areas.

Powerline Inspection

The proposed UAV in the PLUS concept could potentially be used to inspect and monitor cross-country high voltage power lines. The study highlights several aspects that make the shape-adaptive UAV suitable for this application:

1. Endurance enhancement: The primary objective of the PLUS concept is to extend the endurance of fixed-wing UAVs by enabling in-flight energy harvesting from overhead power lines. This extended endurance would allow the UAV to cover longer distances and inspect cross-country power lines more efficiently.

2. Precise powerline tracking: The developed flight dynamics and control framework supports centimeter-scale longitudinal powerline frequency tracking. The UAV can adapt its shape to match the local spatial frequency of the powerline catenary, enabling low-clearance tracking for close inspection.

3. Adaptation to diverse powerline geometries: The study explores the performance of the shape-adaptive UAV across a range of powerline geometries, from low voltage to ultra-high voltage lines. This adaptability makes the UAV suitable for inspecting various types of cross-country power lines.

4. Parameter space exploration: The extensive simulations conducted in the study provide insights into the optimal combinations of aircraft parameters (e.g., wingspan, chord length) for different powerline structures. This knowledge can guide the design of UAVs specifically tailored for inspecting cross-country high voltage power lines.

5. Potential for integration with inspection technologies: The related work section mentions studies on the integration of advanced event-based sensors for fault detection in powerline infrastructure (Rangel et al., 2022). The shape-adaptive UAV could potentially be equipped with similar sensors to enhance its inspection and monitoring capabilities.

However, it is essential to note that the study primarily focuses on the dynamics and control aspects of the shape-adaptive UAV for powerline tracking and energy harvesting. To fully realize the potential of the PLUS concept for cross-country high voltage power line inspection and monitoring, additional research and development would be necessary, such as:

1. Integration of specific inspection sensors and technologies (e.g., visual, infrared, or lidar sensors).
2. Development of algorithms for automated fault detection and analysis based on the collected inspection data.
3. Addressing challenges related to long-distance navigation, communication, and data transmission.
4. Ensuring the UAV's robustness and reliability in diverse weather conditions and operational scenarios.
5. Compliance with relevant regulations and safety standards for UAV operations near high voltage power lines.

In summary, while the PLUS concept UAV demonstrates promise for inspecting and monitoring cross-country high voltage power lines, further research and development would be required to fully adapt the system for this specific application.

Authors

The paper "PowerLine Unmanned Surfer (PLUS): Shape Adaptive Dynamics Development and Control Design" is authored by Ujjval Patel, Francis Phillips, Todd Henry, and Imraan Faruque. The authors are affiliated with the following institutions:

1. Ujjval Patel and Imraan Faruque are with Oklahoma State University, Stillwater, OK, USA.
2. Francis Phillips and Todd Henry are with DEVCOM Army Research Laboratory, Durham, NC, USA.

The work was partially supported by the Army Research Lab under the grant ARL-R-WMRD-300124.

Related work mentioned in the paper covers several areas, including:

1. UAV Endurance Enhancement:
   - Studies on structural adaptation in fixed-wing small UAVs, often inspired by biological systems (Harvey et al., 2022a, b; Cheney et al., 2020; Quinn et al., 2019).
   - Previous surveys on engineered adaptation (Barbarino et al., 2011; Seigler, 2005; Jha and Kudva, 2004).
   - Research on smooth active surfaces replacing internal/external control surfaces (Pankonien and Inman, April 2013; Bilgen et al., 2013).
   - Studies on demanding UAV trajectories and the need for a "trajectory-to-aerodynamic-shape" specification method (Ajaj et al., 2016; Rudnick-Cohen et al., 2022, 2023).

2. Powerline Monitoring Technologies:
   - Exploration of multirotor UAVs for close-range powerline inspections (Dietsche et al., 2021).
   - Integration of advanced event-based sensors for fault detection in powerline infrastructure (Rangel et al., 2022).
   - Adaptive control algorithms for UAVs operating in complex environments (Muñoz-Gómez et al., 2023).

3. Powerline Energy Harvesting:
   - Studies on inductive powerline energy harvesting for wireless sensor networks (Tashiro et al., 2011; Wang and Ha, 2021; Riba et al., 2022).
   - Research on mechanisms for UAVs to physically grasp power lines for energy harvesting and recharging (Iversen et al., 2021a; vom Bögel et al., 2020; Stewart et al., 2022; Stuhne et al., 2022; Iversen et al., 2021b; Nyboe et al., 2023).

4. Adaptive Structures for Maneuver:
   - Studies on perching maneuvers in biological systems (KleinHeerenbrink et al., 2022) and the potential for optimization in UAVs (Castano et al., 16-20 June 2014; Haughn and Inman, 2022).
   - Research on at-speed perching using conventional control surfaces (Moore et al., 2014; Greatwood et al., 2017; Fletcher et al., 2022) and reinforcement learning (Greatwood et al., 2017; Fletcher et al., 2022).
   - Development of vehicles capable of aggressive maneuvering using wing and tail adaptation (Ajanic et al., 2020).

The authors emphasize that the PLUS concept distinguishes itself from previous research by taking advantage of the existing powerline catenary shape to extend the capabilities of fixed-wing UAVs, focusing on the dynamic development aspect and the integration of airframe flight dynamics with shape adaptation for trajectory feasibility assessment.

Shape Adaptive Dynamics Development and Control Design

Ujjval Patel

arxiv.org

---

PowerLine Unmanned Surfer (PLUS):
Shape Adaptive Dynamics Development and Control Design

   Francis Phillips    Todd Henry    and Imraan Faruque U. N. Patel, and I. A. Faruque are with Oklahoma State University, Stillwater, OK 74078 USA (e-mail: ujjval@okstate.edu, i.faruque@okstate.edu). F. R. Phillips, and T. C. Henry are with DEVCOM Army Research Laboratory, 800 Park Offices Drive, Durham, NC 27709 USA (e-mail: francis.r.phillips7.civ@army.mil ,todd.c.henry2.civ@army.mil).The Army Research Lab partially supported this work under ARL-R-WMRD-300124. Copyright by the authors May 2024; this work may be under consideration for publication and copyright may be transferred without notice, after which this version may no longer be accessible.

Abstract

This paper introduces the powerline unmanned surfer (PLUS) concept to extend the limited endurance of fixed wing unmanned aerial vehicles (UAVs) via in-flight energy harvesting from overhead electrical distribution power lines, and develops the flight dynamics and control framework to support centimeter-scale longitudinal powerline frequency tracking. The dynamics framework models the UAV’s shape adaptive structure, aerodynamic forces, and control inputs, and applies the coupled flight mechanics framework to low clearance tracking of powerline contours. This study develops a “trajectory to shape-adaptive UAV” controller design approach for longitudinal powerline tracking through local spatial frequency matching. The frequency-matching approach dynamically regulates the aircraft modes’ frequency to the powerline catenary spatial frequency using a generalized parameter linearization approach. Performance is assessed on an example UAV implementing camber and thickness morphing by quantifying clearance distance from neighborhood to high voltage powerline environments and across span and chord combinations. This approach achieves alternating periods of low-clearance tracking and antiphase oscillation, with 34% of the powerline having tracking error less than 1m. Airfoil thickness increase has a stronger effect over Phugoid mode wavelength than thickness decrease. Wingspan, chord, and powerline parameter sensitivities are quantified, providing a foundation for near-field long-distance powerline tracking and energy harvesting.

1 Introduction

Electric propulsion unmanned aerial vehicles (UAVs) have become integral in applications such as surveillance and payload delivery, yet their endurance and range are limited by the energy constraints of batteries. Although conventional aerial refueling offers partial solutions, its limited efficiency and infrastructure requirements highlight the need for innovative approaches. Traditional UAV design approaches, particularly for fixed wings, often begin with a set of aircraft performance requirements, such as range, endurance, and cruise speed, and later develop maneuverability limits and achievable trajectories via turn rate and speed limitations. This approach focuses on gross aircraft performance rather than precisely tailoring the airframe’s dynamic maneuverability characteristics to a specific mission trajectory. Fundamentally, the dynamically achievable trajectories are not precisely specified as input and are an iteration or an envelope specified by its corners rather than the natural behaviors of the aircraft.

As UAV missions become more diverse, including new prescribed flight maneuvers and trajectories, mechanisms to incorporate maneuverability and trajectory-following in early stage design will be helpful. Applications could include terrain following, flight in caves, or flight in cluttered environments. In such examples, instead of ”what are the achievable trajectories for a given configuration?” the design for extreme behaviors asks ”what airframe configuration(s) are able to achieve a given trajectory?” In some cases, the integration of an additional effector, such as a morphing structure or actuator, could provide a required envelope expansion.

This design approach provides an alternative inverse to traditional configuration design, in which an airframe’s detailed maneuverability characteristics is an outcome of configuration choice and sizing. The design-for-trajectory approach instead uses mission trajectory specification as an input to specify the airframe’s outer mold line, which may include new shape adaptation modalities to achieve new trajectories.

This study introduces the powerline unmanned surfer (PLUS) concept as an early example of this dynamics-integrated UAV design, beginning with mission-specific trajectory requirements. The focus of PLUS on powerline tracking supports UAV endurance improvements by enabling in-flight energy harvesting from overhead electric powerlines. An integrated approach that encompasses structure, aerodynamics, and controls allows prolonged flight and improved mission performance.

A core challenge in the implementation of PLUS lies in the control necessary to track the discontinuous trajectories of the powerlines while maintaining electrical connectivity. This demands an integrated control and dynamics framework, balancing the UAV’s adaptive structure, aerodynamic forces, and control input. The focus of this paper is on this dynamic development aspect– a framework to incorporate airframe flight dynamics and with shape adaptation and assess trajectory feasibility.

This dynamics framework integrates shape adaptive features into a reference airframe, aiming to explore the benefits and challenges of shape adaptiveness in altitude-based powerline tracking. Camber and thickness variation examples are used to explore the relationship between shape adaptiveness and natural aircraft longitudinal flight modes: Phugoid and short period. The natural flight modes of the aircraft are then dynamically tailored to match the local spatial frequency of the hanging utility lines.

A novel trajectory-to-shape adaptive design framework for longitudinal powerline tracking has been introduced, overcoming the limitations of conventional airframes in matching the catenary spatial frequency of powerlines. This framework represents a significant advance in UAV design, enabling real-time morphing of the airfoil geometry to meet the specific demands of powerline tracking. The open-loop control approach is applied to a shape adaptive air vehicle simulation to quantify its performance across a range of utility line environments.

1.1 Previous Work

The PLUS concept connects several areas in which UAVs have received considerable research and development, particularly in the areas of endurance enhancement, adaptive structures, and powerline monitoring.

1.1.1 UAV Endurance Enhancement

Structural adaptation to increase the control authority of fixed wing small UAV is an idea often modeled by biological systems (Harvey et al., 2022a, b; Cheney et al., 2020; Quinn et al., 2019). Considerable previous attention (Seigler and Neal, 2009; Kota et al., 2003) including several previous surveys (Barbarino et al., 2011; Seigler, 2005; Jha and Kudva, 2004). Adding to these detailed surveys is outside the scope of this paper.

Instead, we note that the range of engineered adaptation (and consequently the resulting trajectory) is typically less aggressive than the shape adaptations seen in avian systems. For example, (Cheney et al., 2020) used small wing twist and camber adjustments complemented by tail movements to maintain an optimal trajectory. Compared to conventional UAV, avian systems have higher degrees of articulation using smooth, active surfaces that lack control linkages and hinges at the outer mold line. The degree to which smooth active surfaces can be used to replace various internal/external control surfaces in the wing and tail has been researched by (Pankonien and Inman, April 2013; Bilgen et al., 2013). Even at the comparatively conservative trajectories seen in previous engineered work, these adaptations have suggested a need for a new design philosophy (Ajaj et al., 2016). As UAV missions with more demanding trajectories are addressed as done by (Rudnick-Cohen et al., 2022) and (Rudnick-Cohen et al., 2023), the need for a detailed “trajectory-to-aerodynamic-shape” specification method becomes a more significant limitation.

1.1.2 Powerline Monitoring Technologies

Powerline monitoring has been a critical application area for UAVs. (Dietsche et al., 2021) explored the use of multirotor UAVs for close-range powerline inspections, emphasizing the importance of stable flight dynamics near high-tension lines. The integration of advanced event based sensors for fault detection in powerline infrastructure was highlighted in (Rangel et al., 2022), underscoring the utility of UAV in preventative maintenance.

Flight in close proximity to powerlines poses specialized control challenges. Adaptive control algorithms developed in (Muñoz-Gómez et al., 2023) for UAVs operating in complex environments laid the foundation for precision flight controls. However, these studies focused on the use of quadcopters for powerline inspection and survey while maintaining a safe distance from the powerline infrastructure. These studies did not seek to leverage powerline structures as a means of enhancing UAS capabilities.

1.1.3 Powerline energy harvesting

In-flight powerline energy harvesting could be accomplished from a moving fixed wing UAV via either a trailing contact (“shoe”) or an inductive coil. The magnetic field of a long straight wire is

$$B=\frac{{\mu }_{0}I}{2\pi R},$$

where $I$ is the current, $R$ the distance to the wire, and ${\mu }_0=4\pi \times {10}^{-7}\text{T m/s}$ the permeability of free space. A single 345kV powerline carrying 628A could have a 125$\mu$T magnetic field at 1m (rur, 2008). Inductive powerline energy harvesting has previously been approached for wireless sensor networks, using air-core coil and resonant capacitor circuits to demonstrate 1-6mW energy harvesting from a 21$\mu$T magnetic field switching at 60Hz (Tashiro et al., 2011). These studies showed that the number of coil turns and core material affect the harvesting potential and estimated that energy harvesting levels at publicly acceptable levels could be comparable to photovoltaic cell output on a cloudy day ($130\mu$W/cm³ at 200$\mu$T) (Tashiro et al., 2011; Wang and Ha, 2021). Previous work tailored towards wireless sensor networks has shown scavenging at single amp levels, scavenging via inductors between parallel wires (850$\mu$W from 8.4A differential currents), and highlighted the importance of core choice for higher power densities (100mW/cm³) (Riba et al., 2022).

A UAV in flight may not enclose the wire completely, requiring the inclusion of a demagnetization factor. Work on non-enclosing energy harvesters has previously computed shape optimizations for such cases, such as the bow-tie shaped non-enclosing coil in (Yuan et al., 2015).

Research efforts have explored various approaches to enabling UAVs to interact with power lines for energy harvesting and recharging purposes, focusing on the development of mechanisms for physically grasping power lines. (Iversen et al., 2021a) focused on the design and testing of a mechanical grappling mechanism that allows UAVs to secure their connection to powerlines, providing a stable platform for energy transfer. (vom Bögel et al., 2020) evaluated the feasibility of a drone charging function on overhead power lines and verified this in a test setup. The work of (Stewart et al., 2022) introduced a novel mechanical structure attached to the nose of a light-weight fixed wing aircarft that could extract electrical energy from high-voltage powerlines with minimal loss and convert it to a form that could be used by UAV batteries. (Stuhne et al., 2022)’s presented a novel electromechanical recharging station that can be mounted on energized AC power line to charge the drone battery wirelessly without the need to modify the electrical infrastructure. Meanwhile, (Iversen et al., 2021b) explored the long-term impacts of continuous powerline energy harvesting on UAV battery life and performance, offering insights into optimal charging cycles and energy management strategies. Finally, (Nyboe et al., 2023) presented technologies that allow UAVs to autonomously attach and recharge from the existing DC railway infrastructure.

1.1.4 Adaptive Structures for Maneuver

Fixed wing UAVs typically achieve higher range and endurance relative to similar scale multirotor configurations that can achieve more decoupled motions (Mulgaonkar et al., 2014). One approach to mission endurance improvement is perching at a speed that biological systems typically do with precise control of their velocity and position (KleinHeerenbrink et al., 2022). (KleinHeerenbrink et al., 2022) suggested that trajectory information in combination with aeromechanical information (pressure/strain) (Castano et al., 16-20 June 2014; Haughn and Inman, 2022) and perception (distance/location) could be used to optimize behavior in real time for UAV. (Moore et al., 2014) showed that at speed perching could be done with conventional control surfaces with (Greatwood et al., 2017), and (Fletcher et al., 2022) using sweep control and reinforcement learning to command the desired trajectory. Both (Greatwood et al., 2017) and (Fletcher et al., 2022) were able to, in real-world flight tests, command an approach and flare trajectory near a perch position with reasonable accuracy using reinforcement learning. (Ajanic et al., 2020) developed a vehicle capable of aggressive maneuvering by creating a wing and tail capable of adaptation.

The PLUS concept distinguishes itself from previous research studies by taking advantage of existing powerline catenary shape, thereby extending the existing capabilities of a fixed-wing UAV.

2 Methods & Approach

2.1 Mission space definition

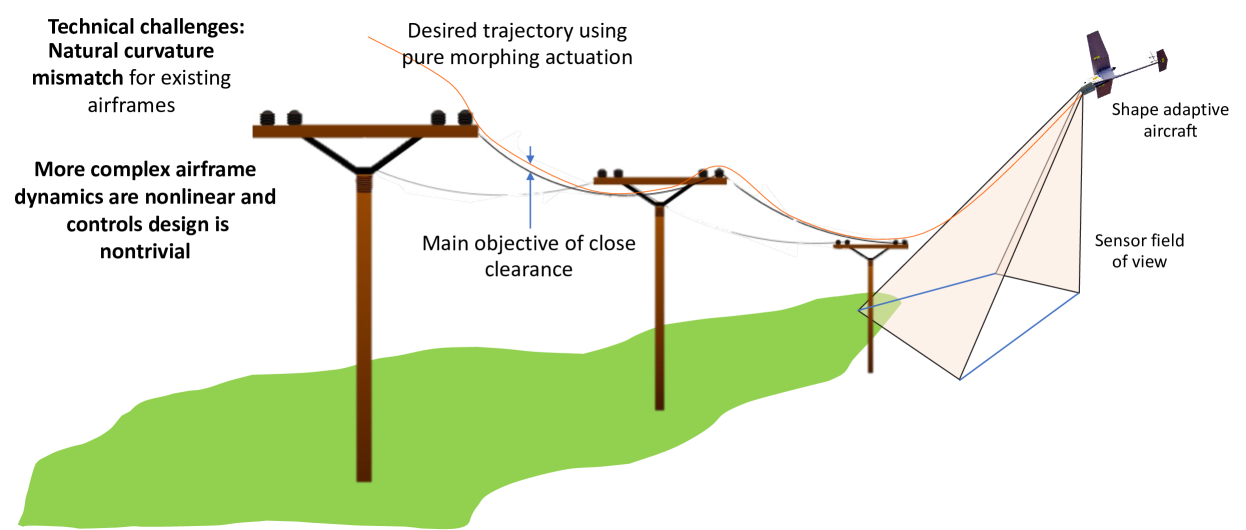
A central feature of this framework is its precision in tracking the catenary contour of powerlines through ”local spatial frequency matching.” This process entails the agile adaptation of the UAV’s spatial frequencies to align with the undulating spatial frequency of the powerlines. The research details a comprehensive dynamic model, accompanied by simulations to quantify the UAV’s longitudinal tracking performance along powerline trajectories. Figure 1 illustrates the operational mission space of the PLUS system, and highlights technical challenges to the PLUS concept.

Figure 1: Powerline unmanned surfing concept for long range fixed wing UAV range extension and navigation.

Figure 2 illustrates the coverage of this paper, showing the interconnection between the flight dynamics model, powerline geometry, and sensing and feedback structure.

Figure 2: This paper’s coverage: flight dynamics model development, powerline geometry environment, and controller development.

2.2 Powerline Modeling

An example powerline catenary curve is illustrated in Fig. 3, in which the between-pole curves are modeled as a catenary influenced by environmental parameters (Farr et al., 1980).

The expression for a powerline catenary curve was given by

$$y=\frac{T_0}{\rho gA}\cosh \left\{\frac{\rho gA}{T_0}\left(x-\frac{L}{2}\right)\right\}\text{for }x\in [0,L],$$

(1)

where $T_0$ is the tension in the cable at ambient temperature, $\rho$ is the density of material in the transmission cable, $A$ is the cross-sectional area of the transmission cable and $g$ is gravitational acceleration. The local curvature of the powerline catenary $R$ can be expressed as

$$R=\frac{T_0}{\rho gA}{\cosh }^2\left\{\frac{\rho gA}{T_0}\left(x-\frac{L}{2}\right)\right\}.$$

Figure 3: Powerline geometry used in this study (Farr et al., 1980).

2.2.1 Local spatial frequency of a catenary

One can find the frequency of the catenary curve based on the assumption that the physical properties of the powerline can be estimated and that the travel speed of is constant as it flies over the powerline. Then, the local spatial frequency of the catenary can be defined as

$${\omega }_s(x)=\frac{x}{y(x)}.$$

(2)

2.3 Aircraft control approach with shape adaptive actuation

Shape adaptive actuation alters an aircraft’s aerodynamics and associated stability derivatives by modifying its physical geometry. Variations induced by shape adaptiveness can be formulated as a perturbation of traditional stability derivatives (Beard et al., 2012) by introducing a vector of generalized time-varying shape adaptive parameters $\sigma (t)$. This approach is further specialized for the purpose of this paper for camber or thickness and span shape adaptation.

This section presents the definition of the linear system and a linearization approach that incorporates adaptive dynamics of the nonlinear shape as an explicit function of $\sigma (t)$. In state-space form, a non-linear system model $\dot{x}=f(x,u,t)$ can be expressed as

$$\dot{x}\approx A[\sigma (t)]x+B\left[\sigma (t)\right]u+W[\sigma (t)]$$

with

$$A[\sigma (t)]={\frac{\partial f(x,u,t)}{\partial x}|}_{x_0}B[\sigma (t)]={\frac{\partial f(x,u,t)}{\partial u}|}_{u_0},$$

where $W[\sigma (t)]$ represents higher-order nonlinear terms, and the state matrices vary with $\sigma (t)$, a time-varying vector that may consist of system outputs, exogenous inputs, or a combination of both. In the sections below, example dynamics of two types of shape adaptive structures for a UAV are discussed, and how they can be used as actuation to control a shape adaptive aircraft is developed.

2.3.1 Example: Airfoil shape adaptation (Camber and Thickness)

The introduction of laterally symmetric, shape-adaptive alterations significantly impacts the longitudinal aerodynamics, particularly the normal force and the pitch moment stability derivatives. The traditional linearized state-space dynamics model can then be written in terms of a generic morphing control input $\sigma (t)$. Consistent with traditional linearized modeling, states are defined in terms of perturbations from trim values. Shape adaptive aircraft having independent shape and flight control, as in a linear system, have been discussed in the literature (Wu et al., 2015). An analogous linearization allows writing force and momentum as

	$m\ddot{x}=$	$-D\cos \alpha +L\sin \alpha +T-mg\sin \theta$
	$m\ddot{w}=$	$-D\sin \alpha -L\cos \alpha +mg\cos \theta$
	$I_{yy}\dot{q}=$	$M_A-gS\sin \theta ,$

where the lift, drag, and moment can be described as

	$L$	$=0.5\rho V^{2}S{C}_L$
	$D$	$=0.5\rho V^{2}S{C}_D$
	$M_A$	$=0.5\rho V^{2}Sc{C}_m.$

The aerodynamic coefficients directly affected by the camber or thickness shape $\mu$ can be written in a $C_{[L,D,m]}(\alpha ,V,\mu )$ form similar to stability derivatives as

	$C_L$	$=C_L(\alpha ,V,\mu )=C_{L0}+C_{L\alpha }\alpha +C_{LV}\mathrm{\Delta }V/V+C_{L\mu }\mu$
	$C_D$	$=C_{D0}+C_{D\alpha }\alpha +C_{D{\alpha }^2}{\alpha }^2+C_{DV}\mathrm{\Delta }V/V+C_{D\mu }\mu$
	$C_m$	$=C_{m0}+C_{m\alpha }\alpha +C_{mV}\mathrm{\Delta }V/V+C_{m\mu }\mu .$

2.3.2 Example: Variable span shape adaptation

The use of variable wingspan to improve flight performance and control authority of high endurance, medium-altitude UAV has been investigated in detail, such as (Ajaj et al., 2009). A linear parameter varying approach similar to (Yue et al., 2013) is used to obtain

	$\ddot{x}$	$=\dot{u}+qw-rv+g\sin \theta$
	$\ddot{y}$	$=\dot{v}+ru-pw+g\cos \theta \sin \varphi$
	$\ddot{z}$	$=\dot{w}+pv-qu+g\cos \theta \cos \varphi$
	$\dot{\varphi }$	$=p+tan\theta (q\sin \varphi +r\cos \varphi )$
	$\dot{\theta }$	$=q\cos \varphi -r\sin \varphi$
	$\dot{\psi }$	$=(q\sin \varphi +r\cos \varphi )\sec \theta$
	$p$	$=\dot{\varphi }-\dot{\psi }\sin \theta$
	$q$	$=\dot{\theta }\cos \varphi +\dot{\psi }\cos \theta \sin \varphi$
	$r$	$=\dot{\psi }\cos \theta \cos \varphi -\dot{\theta }\sin \varphi$

	${\displaystyle \sum L}$	$={\displaystyle \sum (L_0+\mathrm{\Delta }L)}=\dot{p}{I}_x+p{\dot{I}}_x-\dot{q}{I}_{xy}-q{\dot{I}}_{xy}-\dot{r}{I}_{xz}$
		$-r{\dot{I}}_{xz}-qp{I}_{xz}-q^2{I}_{yz}+qr{I}_z-rq{I}_y+r^2{I}_{yz}$
	${\displaystyle \sum M}$	$={\displaystyle \sum (M_0+\mathrm{\Delta }M)}=\dot{q}{I}_y+q{\dot{I}}_y-\dot{p}{I}_{xy}-p{\dot{I}}_{xy}-\dot{r}{I}_{yz}$
		$-r{\dot{I}}_{yz}+rq{I}_x-rq{I}_x-r^2{I}_{xz}+p^2{I}_{xz}+pq{I}_{yz}-rq{I}_z$
	${\displaystyle \sum N}$	$={\displaystyle \sum }(N_0+\mathrm{\Delta }N)==\dot{r}{I}_z+r{\dot{I}}_z-\dot{p}{I}_{xz}-p{\dot{I}}_{xz}-\dot{q}{I}_{yz}$
		$-q{\dot{I}}_{yz}-p^2{I}_{xy}+pq{I}_y-pr{I}_{yz}-qp{I}_x+q^2{I}_{xy}+qr{I}_{xz}.$

Assuming the adaptation of the symmetric span shape and using $\delta y$ and $\delta \dot{y}$ as the adaptive parameters of the shape, we arrive at

	${\displaystyle \sum L}$	$=\dot{p}{I}_{x0}+qr(I_{z0}-I_{y0})+2m_s\dot{\delta }y(y_{0}p+\delta yp)$		(3)
	${\displaystyle \sum M}$	$=\dot{q}{I}_{y0}+rq(I_{x0}-I_{z0})$		(4)
	${\displaystyle \sum N}$	$=\dot{r}{I}_{z0}+pq(I_{y0}-I_{x0})+2m_s\dot{\delta }y(y_{0}r+\delta yr).$		(5)

The linearized aircraft model augmented with non-linear shape adaptation thickness and span shape $\sigma =[\mu ,\delta y,\delta \dot{y}]$ can be written in terms of normalized aerodynamic stability derivatives as

$$\left[\begin{array}{c}\dot{u}\\ \dot{w}\\ \dot{q}\\ \dot{\theta }\\ \dot{h}\end{array}\right]=\left[\begin{array}{ccccc}{X}_u(\sigma )& X_w(\sigma )& X_q& -g\cos {\theta }_0& 0\\ Z_u(\sigma )& Z_w(\sigma )& u_0& -g\sin {\theta }_0& 0\\ M_u(\sigma )& M_w(\sigma )& M_q(\sigma )& 0& 0\\ 0& 0& 1& 0& 0\\ \cos {\theta }_0& \sin {\theta }_0& 0& 0& 0\end{array}\right]\left[\begin{array}{c}u\\ w\\ q\\ \theta \\ h\end{array}\right].$$

(6)

2.3.3 Structural Actuation

Shape-adaptive aircraft must include an actuation mechanism. Servos are commonly used to modify the airfoil shape. A second-order transfer function with delay was used to represent the servo, and a slew-rate limit was also included (Wada et al., 2009).

3 Catenary frequency mapping control design

Flight speeds between pylons are in the range of 1-3 seconds, placing them near the Phugoid mode of a Group 1 UAV (United States. Army. Unmanned Aircraft Systems. Center of Excellence, 2010). The Phugoid mode describes a tradeoff between airspeed and altitude, and leveraging this natural mode may be an especially relevant method of achieving the height variation needed for powerline tracking. A concise control architecture can be developed using aerodynamic shape adaptation to match the Phugoid mode’s temporal frequency to the local powerline spatial frequency in Equation (2). The powerline’s local spatial frequency prescribes the required aerodynamic shape for close tracking; equivalently, the Phugoid’s spatial wavelength is modulated to match the powerline.

To implement this frequency-matching approach, Equation (6) is linearized with respect to the nonlinear shape adaptive parameter $\sigma (t)$ about ${\sigma }_0=0$ to obtain

	$\dot{x}(t)$	$=Ax(t)+B_{\sigma }\sigma (t)x(t),$
		$=\left[A+B_{\sigma }\sigma (t)\right]x(t),$		(7)

with

	$A$	$=\left[\begin{array}{ccccc}{X}_u& X_w& X_q& -g\cos {\theta }_0& 0\\ Z_u& Z_w& Z_q& -g\sin {\theta }_0& 0\\ M_u& M_w& M_q& 0& 0\\ 0& 0& 1& 0& 0\\ \sin \theta & -\cos \theta & 0& u\cos \theta +w\sin \theta & 0\end{array}\right],$
	$B_{\sigma }$	$=\left[\begin{array}{ccccc}{X}_{u\sigma }& X_{w\sigma }& 0& 0& 0\\ Z_{u\sigma }& Z_{w\sigma }& 0& 0& 0\\ M_{u\sigma }& M_{w\sigma }& M_{q\sigma }& 0& 0\\ 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0\end{array}\right].$

Analyzing the long period mode from Eqn. (7), the Phugoid (temporal) frequency is

$${\omega }_t(\sigma )=\sqrt{\frac{g(Z_u+Z_{u\sigma }(\alpha ,\sigma )\sigma )}{Z_q}}.$$

(8)

The catenary’s local spatial frequency ${\omega }_s$ can be used to find the required shape adaptation analytically, first as a requirement on the aircraft Phugoid frequency ${\omega }_t$, then via aerodynamic sensitivity as a requirement on the morphing parameter $\sigma$. The spatial frequency matching requirement is

$${\omega }_s(x)=\frac{1}{u_0}{\omega }_t(\sigma ),$$

(9)

or, substituting Eqn. (2) and (8) into (9),

$$\frac{u_{0}x}{y(x)}=\sqrt{\frac{g(Z_u+Z_{u\sigma }(\sigma ,\alpha )\sigma )}{Z_q}}.$$

Solving for terms dependent on morphing $\sigma$, one has

$$Z_{u\sigma }(\sigma ,\alpha )\sigma =\frac{Z_q{u}_0^2{x}^2}{gy{(x)}^2}-Z_u.$$

which can be simplified to

$$Z_{u\sigma }(\sigma ,\alpha )\sigma -\frac{Z_q{u}_0^2{x}^2}{gy{(x)}^2}+Z_u=0.$$

(10)

Using the lookup table for a given set of the angle of attack $\alpha$ and the aerodynamic parameters $Z_{u\sigma }$, Eqn. (10) can be solved using numerical solvers such as Newton Raphson method to extract an adaptive parameter of the analytical shape as a function of the distance traveled from the post, provided that there is post-inflection point. The resulting feedforward controller architecture is shown in Fig. 4.

Figure 4: Controller architecture for phugoid-catenary mapping

3.1 Design Simulations

To generalize airframe selection and the range of shape adaptive structures needed, using the definition of mission space and the phugoid-catenary matching controller for a generic reference aircraft example chosen through trial and error in simulation that gives adequate results and using that as a base, a trend search is performed using unconstrained nonlinear least squares-based optimization to get us aerodynamic parameters required for a given powerline structure.

The optimization performed is

$$\widehat{\sigma }(t)\in {\text{argmin}}_{\sigma }\sum _{i=1}^{i=N}{[s_{\text{ref}}-s(x(t),\sigma (t_i))]}^2,$$

where $s_{\text{ref}}$ is the reference powerline trajectory (here assumed known at a given time and location) and $s(x(t),\sigma (t_i))$ is the actual trajectory for the aircraft for a given time series of morphing $\sigma (t_i)$ and the aircraft state $x(t)$.

3.1.1 Simulation Case Study: Generic aircraft (Group I type)

Shape Adaptive Aircraft Design

This study simulated a reference aircraft that includes variations in airfoil camber and airfoil thickness. A nominal NACA2412 airfoil capable of adapting to the shape from NACA1412 to NACA4416 for the maximum camber location change and from NACA2406 to NACA2416 for thickness change.

Figure 5: Shape adaptive solver in loop method of aerodynamic parameter calculation

Figure 6: Pre computed shape adaptive aerodynamic parameter calculation

To simulate continuous shape adaptive aerodynamics, XFoil and Matlab were used to characterize the aerodynamic parameters for the aircraft flight envelope using two methods as illustrated in Fig. 5 and Fig. 6, where the stability derivatives related to shape adaptive parameters are calculated in loop and pre-calculated using prior knowledge of shape adaption limits ($\underset{¯}{\sigma },\overline{\sigma }$) where $\underset{¯}{\sigma }$ is the lower limit of morphing and $\overline{\sigma }$ is the upper limit of the morphing parameter.

The method results in aerodynamic stability derivatives as functions of shape adaptive parameters. A example of Eqn. (7) maneuvering about trim is

$$\begin{array}{c}\hfill \left[\begin{array}{c}\dot{u}\\ \dot{w}\\ \dot{q}\\ \dot{\theta }\\ \dot{h}\end{array}\right]=(\left[\begin{array}{ccccc}-0.074& -0.122& 0& -9.811& 0\\ -1.535& -7.457& 25& 0& 0\\ 2.689& -5.850& -32.945& 0& 0\\ 0& 0& 1& 0& 0\\ 1& 0& 0& 0& 0\end{array}\right]+\\ \hfill \left[\begin{array}{ccccc}-0.332& -2.096& 0& 0& 0\\ -3.960& -15.336& 0& 0& 0\\ 25.329& 95.192& -160.32& 0& 0\\ 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0\end{array}\right]\sigma )\left[\begin{array}{c}u\\ w\\ q\\ \theta \\ h\end{array}\right].\end{array}$$

(11)

Simulation Method

To illustrate the proposed controller operation, this approach is implemented in MATLAB, where a high-fidelity nonlinear shape adaptive aircraft is simulated with the control input developed using a linearized shape adaptive aircraft dynamics representation as developed above. The simulation includes a reference power line with 30m tall towers spaced at 70m intervals.

The controller has local information about the powerline geometry to estimate the catenary spatial frequency and full state information about the aircraft from the dynamics to predict the Phugoid temporal frequency for phugoid-catenary mapping; the controller is re-initialized when crossing each tower.

3.1.2 Numerical parameter space exploration

To optimize the design of the powerline unmanned surfer (PLUS) for diverse operational environments, simulations to explore the interplay between different aircraft design parameters and various powerline structures were conducted. This step was instrumental in identifying the most effective combinations of aircraft wingspan and chords for powerline tracking performance across a range of powerline geometries.

The trend search involved running a series of simulations, each iterating over a set of predefined span and chord values for the UAV. These values were tested against multiple powerline structures, characterized by different catenary curve parameters such as sag, tension, and span length. The primary objective was to determine how changes in the UAV’s physical dimensions influenced its ability to adapt and maintain efficient tracking of the powerlines, especially in varying environmental conditions.

Aircraft parameters

The simulations systematically varied two UAV parameters: chord length and wingspan. The wing’s chord (leading edge to trailing edge distance) was varied, exploring the effects of change in chord length for group I type UAVs. The chord lengths varied from $0.203\text{m}$ to $0.305\text{m}$ with increment of $0.51\text{m}$. The wingspan (distance between the tips of the wings) was altered in each simulation run, testing a range of typical Group I UAVs. Wingspans ranged from $1\text{m}$ to $1.8\text{m}$ with increments of $0.4\text{m}$

Environmental parameters

The variations were evaluated across a spectrum of powerline geometries ranging from low voltage to ultra high voltage (¿800kV), as outlined in Table 1, to quantify the spacing and height dimensions of the pylons. Furthermore, the impact of environmental factors on the powerlines was standardized by the percentage of sag throughout the pylon span.

Table 1: Powerline class and structural parameters (ESRI U.S. Federal Datasets, 2022).

This approach provided a mechanism to quantify the UAV’s performance across varying environmental geometry.

4 Results and discussion

4.1 Thickness morphing experiment

A representative servo actuation system was manufactured and the identification of the time domain system was used to determine the transfer function from the experimental data. The experiment used the additively manufactured airfoil shown in Fig. 7 which has a degree of freedom of thickness actuated by the servo. A camera operating at 120 frames per second was used to digitize the thickness variation using the MATLAB image processing toolbox (The MathWorks Inc., 2022). The actuator system received a multistep input command and the recorded input/output signals were used to quantify the response time, the maximum deflection angles, and the effects of the slew rate limit of $0.11s/{60}^{\circ }$ degree rotation.

Figure 7: Thickness morphing airfoil actuator used in experimental identification

A multiple-step stimulus of $3^{\circ }$ servo deflection was used for identification, and the identification of the time-domain system considered three transfer function model structures: first order, second order system, and second order with time delay. The identification results in Table 2 indicate that a 2nd order model including transport delay best describes the response.

Table 2: Structural actuation system identification results

The identified thickness morphing transfer function was

$$Y(s)=\frac{0.01333}{s^2-1.838s+1}\left(1-e^{-0.005s}\right),$$

(12)

as seen in Fig. 8.

Figure 8: Morphing data fit to a second order system with time delay

4.2 Simulation results

The results of the aircraft trajectory based on the implemented controller are shown in Fig. 9. The tracking of the power line is achieved periodically in alternating troughs, leading to low and high levels of cyclic clearance, as shown by the shaded regions in Fig. 9. The powerline clearance shown in Fig. 10 shows that for the chosen aircraft the variation of - 3% to 6.3% of the camber or the variation of -3.2% to 5.5% thickness shown in Fig. 12 achieves ¡1m powerline spacing for 88.7m of the 260m span, or 34% of the longitudinal region. Fig. 11 shows the velocity deviation during the controller implementation.

Figure 9: Powerline tracking for shape adaptive aircraft

Figure 10: Error between aircraft trajectory and powerline

Figure 11: Velocity deviation for the powerline tracking

Figure 12: Continuous shape adaptive input to the system for powerline tracking

4.3 Parameter space exploration

The parameter space exploration examined the sensitivity to wingspan, powerline span, and wing chord. The proficiency requirement is quantified using the maximum aerodynamic change required by a morphing that is found by considering the unmorphed aerodynamic coefficient relative to the maximal morphing seen in the trial. For example, for the case of lift coefficient $C_L$, the maximal $C_L$ variation observed is found by parameterising lift coefficient as a function of morphing, eg $C_L(\alpha ,\sigma )$. Then, we find the maximum morphing parameter value and the time at which it occurs, eg, defining

	$t_m$	$=\arg \underset{t}{\max }\sigma (t),\forall t\in [0,t_f]$		(13)
	$\overline{\sigma }$	$=\underset{t}{\max }\sigma (t),\forall t\in [0,t_f]$		(14)

for a trial lasting from time $t=0$ to final time $t_f$, then the maximum change in lift coefficient demanded by morphing in that trial is

$$\mathrm{\Delta }{C}_{L,m}=C_L(\alpha (t_m),\overline{\sigma })-C_L({\alpha }_0,0),$$

where ${\alpha }_0$ denotes the trimmed angle of attack.

$\mathrm{\Delta }{C}_{L,m}$ was computed for a total of 4,500 cases, covering 25 trials for each combination of 4 pylon span distances that cover LV to EHV powerlines, 3 airfoil chords, 3 aircraft wingspans and 5 sag level combinations.

Figure 13: Parameter space exploration results for LV powerlines (40m pylon span)

Figure 14: Parameter space exploration results for MV powerlines (100m pylon span)

Figure 15: Parameter space exploration results for HV powerlines (300m pylon span)

Figure 16: Parameter space exploration results for EHV powerlines (500m pylon span)

Mean morphing-driven changes in $C_L$ (as quantified by $\max |\mathrm{\Delta }{C}_{L,m}|$) increases with decreases in either mean aerodynamic chord (MAC) decreases or wing area, with the area effect is most visible in Fig. 16. Both are likely related to the need for higher lift coefficients on smaller aerodynamic surfaces.

Across Figs. 13-16, the 2% powerline sag results consistently show lower $\max \mathrm{\Delta }{C}_{L,m}$ requirements. This lower actuation requirement is likely due to the 2% sag powerline wavelengths being near an integer factor of the aircraft’s Phugoid wavelength. This effect is illustrated for the cases $d=100$ m and $d=300$ m in Fig. 17. This lowered aerodynamic actuation when Phugoid and aircraft wavelength is matched lends support for the frequency-matching approach to control, and Section 4.4 analyzes this relationship.

Figure 17: Illustration of lowered aerodynamic actuation needed for powerline wavelengths being near an integer factor of the aircraft’s (c=0.254m, b=1.4m) Phugoid wavelength

4.4 Phugoid wavelength variation

Figure 18 shows the Phugoid wavelength ${\lambda }_{\text{ph}}$ as a function of wing span, chord, and morphed thickness calculated using the Eqn. (15),

$${\lambda }_{\text{ph}}=\frac{u_0}{{\omega }_t(\sigma ,b,c)}$$

(15)

where, ${\omega }_t(\sigma ,b,c)$ is the temporal frequency of a aircraft with wing span $b$ and chord length $c$ at a given morphed thickness of $\sigma$ flying at a trim speed of $u_0$.

Figure 18: Phugoid wavelength during thickness morphing ($\sigma =\pm 14\%$ thickness) shows the authority of thickness morphing over Phugoid length relative to span $b$ and chord $c$ variation.

Fig. 18 indicates that thickness morphing significantly affects Phugoid wavelength, and is a viable control term for matching aircraft modes to powerline spans. Combined with Table 1, Fig. 18 can be used to identify the feasible powerline/airframe pairings for close-range tracking and to estimate the required thickness morphing range.

Figure 19: Phugoid wavelength during thickness morphing ($\sigma =\pm 14\%$ thickness) shows the authority of thickness morphing over Phugoid length relative to aspect ratio

Figure 19 shows that an increase in thickness provides more authority over the Phugoid wavelenth than a comparable decrease in thickness. This increased effectiveness is likely related to the higher aerodynamic sensitivity of thicker airfoils through increased lift and drag. Support for the increase in aerodynamic sensitivity origin is also seen in that thickness morphing has higher authority over Phugoid wavelength when both spans and chord are high, as visible in Fig. 18. However, thickness authority is not simply a function of wing area–Fig. 19 also shows reduced authority at higher aspect ratios.

4.5 Limitations and assumptions

The open loop (feedforward) structure of this control approach does not yet account for parameter uncertainty or measurement noise, and incorporating a sensor-based feedback controller with a dynamic estimator could yield improvements. The approach leverages actuation through a generalized aerodynamic change; thus, camber or thickness and span shape is a design choice. The finding that these modes are feasible does not indicate that other actuation modes are infeasible; rather, alternate paths may achieve this variation, including traditional empennage actuation for spans greater than 300m. Similarly, while higher-fidelity wind tunnel and experimental aerodynamic studies may improve the accuracy of aerodynamic parameter variation relative to panel methods, the frequency matching framework introduced here remains feasible when the configuration change is able to modulate aerodynamic force magnitude (Koreanschi et al., 2016; Galffy et al., 2019).

5 Conclusion

This study presents a concise dynamic model and simulation of a shape-adaptive aircraft capable of camber thickness and span shape designed for a challenging longitudinal powerline tracking mission, such as inflight recharging and perching to the powerline for extension of the flight range. The aerodynamic parameters of the aircraft are directly dependent on the time-varying aerodynamic forces and moments, which are a function of the change in the shape of the wing by the shape adaptive command ($\mu$-camber or thickness adaptive parameter). The coupled longitudinal dynamic equation of the shape adaptive process is derived by simplifying the longitudinal dynamic responses of the wing shape adaptive process. Quasi-steady aerodynamic assumptions are used to numerically simulate the dynamics.

A novel approach in this study is the implementation of a frequency-matching (or wavelength-matching) technique that dynamically adjusts the local temporal frequencies of the aircraft’s natural modes to match the spatial frequency of the powerline’s catenary curve. This was achieved through the generalized linearization of the adaptive parameters of the shape. The results demonstrate the potential for a control strategy capable of achieving alternating periods of low clearance tracking and antiphase oscillation. Furthermore, we integrated an open-loop control strategy that manipulates camber or thickness to maintain less than $1$ meters of powerline clearance for more than 34% of the line, despite the challenges of alternating coverage. This dynamics and controller development lays a strong foundation for low clearance powerline tracking. Additionally, our findings suggest that for group I Unmanned Aerial Vehicles (UAVs) operating at EHV (Extra High Voltage) levels and above, intricate shape adaptation may not be required in order to fly low clearance energy harvesting trajectories. This insight could simplify the design and operation of UAVs for specific applications, reducing the complexity and enhancing the reliability of energy harvesting missions in these high voltage environments.

References

• Harvey et al. (2022a) C. Harvey, V. Baliga, J. Wong, D. Altshuler, and D. Inman, “Birds can transition between stable and unstable states via wing morphing,” Nature, vol. 603, pp. 648–656, 2022.
• Harvey et al. (2022b) C. Harvey, L. Gamble, C. Bolander, D. Hunsaker, J. Joo, and D. Inman, “A review of avian-inspired morphing for uav flight control,” Progress in Aerospace Sciences, vol. 132, pp. 1–27, 2022.
• Cheney et al. (2020) J. Cheney, J. Stephenson, N. Durston, J. Song, J. Usherwood, R. Bomphrey, and S. Windsor, “Bird wing act as suspension system that rejects gusts,” Proceedings of the Royal Society of London, vol. 278, pp. 1–9, 2020.
• Quinn et al. (2019) D. Quinn, D. Kress, E. Chang, A. Stein, M. Wegrzynski, and D. Lentink, “How lovebirds maneuver through lateral gusts with minimal visual information,” Proceedings of the National Academy of Sciences, vol. 116, no. 30, pp. 15 033–15 041, 2019.
• Seigler and Neal (2009) T. Seigler and D. Neal, “Analysis of transition stability for morphing aircraft,” Journal of guidance, control, and dynamics, vol. 32, no. 6, pp. 1947–1954, 2009.
• Kota et al. (2003) S. Kota, J. A. Hetrick, R. Osborn, D. Paul, E. Pendleton, P. Flick, and C. Tilmann, “Design and application of compliant mechanisms for morphing aircraft structures,” in Smart structures and materials 2003: industrial and commercial applications of smart structures technologies, vol. 5054.   SPIE, 2003, pp. 24–33.
• Barbarino et al. (2011) S. Barbarino, O. Bilgen, R. M. Ajaj, M. I. Friswell, and D. J. Inman, “A review of morphing aircraft,” Journal of intelligent material systems and structures, vol. 22, no. 9, pp. 823–877, 2011.
• Seigler (2005) T. M. Seigler, “Dynamics and control of morphing aircraft,” Ph.D. dissertation, Virginia Tech, 2005.
• Jha and Kudva (2004) A. K. Jha and J. N. Kudva, “Morphing aircraft concepts, classifications, and challenges,” in Smart structures and materials 2004: industrial and commercial applications of smart structures technologies, vol. 5388.   SPIE, 2004, pp. 213–224.
• Pankonien and Inman (April 2013) A. Pankonien and D. Inman, “Experimental testing of spanwise morphing trailing edge concept,” in SPIE Smart Structures and Materials + Nondestructive Evaluation and Health Monitoring, vol. San Diego, CA, United States, April 2013, pp. 1–14.
• Bilgen et al. (2013) O. Bilgen, L. Butt, S. Day, C. Sossi, J. Weaver, A. Wolek, W. Mason, and D. Inman, “A novel unmanned aircraft with solid-state control surfaces: Analysis and flight demonstration,” Journal of Intelligent Material Systems and Structures, vol. 24, no. 2, pp. 147–167, 2013.
• Ajaj et al. (2016) R. M. Ajaj, C. S. Beaverstock, and M. I. Friswell, “Morphing aircraft: The need for a new design philosophy,” Aerospace Science and Technology, vol. 49, pp. 154–166, 2016.
• Rudnick-Cohen et al. (2022) E. S. Rudnick-Cohen, J. D. Hodson, G. W. Reich, A. M. Pankonien, and P. S. Beran, “Robust optimal design and control of a maneuvering morphing airfoil,” Journal of Aircraft, vol. 59, no. 4, pp. 861–874, 2022. [Online]. Available: https://doi.org/10.2514/1.C036440
• Rudnick-Cohen et al. (2023) E. S. Rudnick-Cohen, G. W. Reich, A. M. Pankonien, and P. S. Beran, “Robust optimal design and trajectory planning of an aircraft with morphing airfoil sections,” Structural and Multidisciplinary Optimization, vol. 66, no. 10, p. 214, 2023.
• Dietsche et al. (2021) A. Dietsche, G. Cioffi, J. Hidalgo-Carrió, and D. Scaramuzza, “Powerline tracking with event cameras,” 2021 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), pp. 6990–6997, 2021.
• Rangel et al. (2022) R. K. Rangel, A. L. Maitelli, V. A. Rodrigues, and D. R. G. Valente, “Smart cities - automatic power lines inspection,” 2022 IEEE Aerospace Conference (AERO), pp. 1–14, 2022.
• Muñoz-Gómez et al. (2023) A.-M. Muñoz-Gómez, J.-M. Marredo-Píriz, J. Ballestín-Fuertes, and J.-F. Sanz-Osorio, “A novel charging station on overhead power lines for autonomous unmanned drones,” Applied Sciences, vol. 13, no. 18, 2023.
• rur (2008) “Appendix h – electric and magnetic fields (psc overview),” 2008. [Online]. Available: https://www.rd.usda.gov/sites/default/files/UWP_WI64-Dairyland_CapXHRLC_FEIS-AppH.pdf
• Tashiro et al. (2011) K. Tashiro, H. Wakiwaka, S.-i. Inoue, and Y. Uchiyama, “Energy harvesting of magnetic power-line noise,” IEEE Transactions on Magnetics, vol. 47, no. 10, pp. 4441–4444, 2011.
• Wang and Ha (2021) J. Wang and D. S. Ha, “A wide input power line energy harvesting circuit for wireless sensor nodes,” in 2021 IEEE International Symposium on Circuits and Systems (ISCAS).   IEEE, 2021, pp. 1–5.
• Riba et al. (2022) J.-R. Riba, M. Moreno-Eguilaz, and S. Bogarra, “Energy harvesting methods for transmission lines: A comprehensive review,” Applied Sciences, vol. 12, no. 21, p. 10699, 2022.
• Yuan et al. (2015) S. Yuan, Y. Huang, J. Zhou, Q. Xu, C. Song, and P. Thompson, “Magnetic field energy harvesting under overhead power lines,” IEEE transactions on power electronics, vol. 30, no. 11, pp. 6191–6202, 2015.
• Iversen et al. (2021a) N. Iversen, A. Kramberger, O. B. Schofield, and E. Ebeid, “Novel power line grasping mechanism with integrated energy harvester for uav applications,” in 2021 IEEE International Symposium on Safety, Security, and Rescue Robotics (SSRR), 2021, pp. 34–39.
• vom Bögel et al. (2020) G. vom Bögel, L. Cousin, N. Iversen, E. S. M. Ebeid, and A. Hennig, “Drones for inspection of overhead power lines with recharge function,” in 2020 23rd Euromicro Conference on Digital System Design (DSD), 2020, pp. 497–502.
• Stewart et al. (2022) W. Stewart, D. Floreano, and E. Ebeid, “A lightweight device for energy harvesting from power lines with a fixed-wing uav,” in 2022 International Conference on Unmanned Aircraft Systems (ICUAS), 2022, pp. 86–93.
• Stuhne et al. (2022) D. Stuhne, V. D. Hoang, G. Vasiljevic, S. Bogdan, Z. Kovacic, A. Ollero, and E. S. M. Ebeid, “Design of a wireless drone recharging station and a special robot end effector for installation on a power line,” IEEE Access, vol. 10, pp. 88 719–88 737, 2022.
• Iversen et al. (2021b) N. Iversen, A. Kramberger, O. B. Schofield, and E. Ebeid, “Pneumatic-mechanical systems in uavs: Autonomous power line sensor unit deployment,” in 2021 IEEE International Conference on Robotics and Automation (ICRA), 2021, pp. 548–554.
• Nyboe et al. (2023) F. F. Nyboe, N. H. Malle, G. v. Bögel, L. Cousin, T. Heckel, K. Troidl, A. S. Madsen, and E. Ebeid, “Towards autonomous uav railway dc line recharging: Design and simulation,” in 2023 IEEE International Conference on Robotics and Automation (ICRA), 2023, pp. 3310–3316.
• Mulgaonkar et al. (2014) Y. Mulgaonkar, M. Whitzer, B. Morgan, C. M. Kroninger, A. M. Harrington, and V. Kumar, “Power and weight considerations in small, agile quadrotors,” in Micro- and Nanotechnology Sensors, Systems, and Applications VI, T. George, M. S. Islam, and A. K. Dutta, Eds., vol. 9083, International Society for Optics and Photonics.   SPIE, 2014, p. 90831Q. [Online]. Available: https://doi.org/10.1117/12.2051112
• KleinHeerenbrink et al. (2022) M. KleinHeerenbrink, L. France, C. Brighton, and G. Taylor, “Optimization of avian perching manoeuvres,” Nature, vol. 607, pp. 91–96, 2022.
• Castano et al. (16-20 June 2014) L. Castano, S. Airoldi, T. McKenna, and J. Humbert, “Gust rejection using force adaptive feedback for roll,” in 14th AIAA Aviation Technology, Integration, and Operations Conference, vol. Atlanta, Georgia, 16-20 June 2014, pp. 1–15.
• Haughn and Inman (2022) K. Haughn and D. Inman, “Autonomous learning in a pseudo-episodic physical environment,” Journal of Intelligent and Robotic Systems, vol. 104, no. 32, pp. 1–14, 2022.
• Moore et al. (2014) J. Moore, R. Cory, and R. Tedrake, “Robust post-stall perching with a simple fixed-wing glider using lqr-trees,” Bioinspiration and Biomimetics, vol. 9, pp. 1–16, 2014.
• Greatwood et al. (2017) C. Greatwood, A. Waldock, and T. Richardson, “Perched landing manoeuvres with a variable sweep wing uav,” Aerospace Science and Technology, vol. 71, pp. 210–520, 2017.
• Fletcher et al. (2022) L. Fletcher, R. Clarke, T. Richardson, and M. Hansen, “Improvements in learning to control perched landings,” The Aeronautical Journal, vol. 126, pp. 1101–1123, 2022.
• Ajanic et al. (2020) E. Ajanic, M. Feroskhan, S. Mintchev, F. Noca, and D. Floreano, “Bioinspired wing and tail morphing extends drone flight capabilities,” Science Robotics, vol. 5, pp. 1–12, 2020.
• Farr et al. (1980) H. Farr, U. S. D. of the Interior. Water, and P. R. Service, Transmission Line Design Manual, ser. Water resource publication.   U.S. Department of the Interior, Water and Power Resources Service, 1980. [Online]. Available: https://books.google.com/books?id=s7uW1izxtxIC
• Beard et al. (2012) R. W. Beard, R. W. Beard, and T. W. McLain, Small unmanned aircraft: theory and practice.   Princeton: Princeton University Press, 2012.
• Wu et al. (2015) Z. Wu, J. Lu, J. Rajput, J. Shi, and W. Ma, “Adaptive neural control based on high order integral chained differentiator for morphing aircraft,” Mathematical Problems in Engineering, vol. 2015, pp. 1–12, 10 2015.
• Ajaj et al. (2009) R. Ajaj, M. Friswell, E. S. Flores, O. Little, and A. Isikveren, “Span morphing: A conceptual design study,” Structures, Structural Dynamics and Materials Conference, 2009.
• Yue et al. (2013) T. Yue, L. Wang, and J. Ai, “Longitudinal linear parameter varying modeling and simulation of morphing aircraft,” Journal of Aircraft, vol. 50, no. 6, pp. 1673–1681, 2013.
• Wada et al. (2009) T. Wada, M. Ishikawa, R. Kitayoshi, I. Maruta, and T. Sugie, “Practical modeling and system identification of r/c servo motors,” in 2009 IEEE Control Applications, (CCA) & Intelligent Control, (ISIC), 2009, pp. 1378–1383.
• United States. Army. Unmanned Aircraft Systems. Center of Excellence (2010) United States. Army. Unmanned Aircraft Systems. Center of Excellence, “U.s. army unmanned aircraft systems roadmap 2010-2035,” Jan. 2010. [Online]. Available: https://rosap.ntl.bts.gov/view/dot/18249
• ESRI U.S. Federal Datasets (2022) ESRI U.S. Federal Datasets, “U.S. Electric Power Transmission Lines,” https://hub.arcgis.com/datasets/fedmaps::u-s-electric-power-transmission-lines/about, 2022.
• The MathWorks Inc. (2022) The MathWorks Inc., “Matlab: Image processing and computer vision (r2022b),” Software available from MathWorks, 2022, natick, Massachusetts, United States. [Online]. Available: https://www.mathworks.com
• Koreanschi et al. (2016) A. Koreanschi, O. Sugar-Gabor, and R. Botez, “Numerical and experimental validation of a morphed wing geometry using price-païdoussis wind-tunnel testing,” The Aeronautical Journal, vol. 120, no. 1227, p. 757–795, 2016.
• Galffy et al. (2019) A. Galffy, M. Böck, and A. Kugi, “Nonlinear 3d path following control of a fixed-wing aircraft based on acceleration control,” Control Engineering Practice, vol. 86, pp. 56–69, 2019. [Online]. Available: https://www.sciencedirect.com/science/article/pii/S0967066119300309